23.2 第4课时 坡度问题及一次函数k的几何意义(共24张PPT)
文档属性
| 名称 | 23.2 第4课时 坡度问题及一次函数k的几何意义(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 952.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
第23章
解直角三角形
沪科版数学九年级上册
23.2
解直角三角形及其应用
第4课时
坡度问题及一次函数
k
的几何意义
1.理解并掌握坡度、坡比的定义;(重点)
2.学会用坡度、坡比解决实际问题.(难点)
学习目标
本节目标
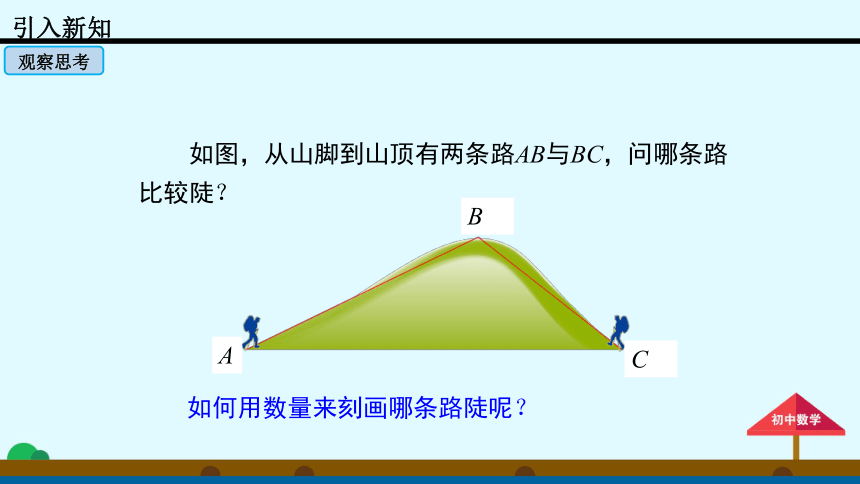
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
A
B
C
引入新知
观察思考
α
l
h
i=
h
:
l
1.
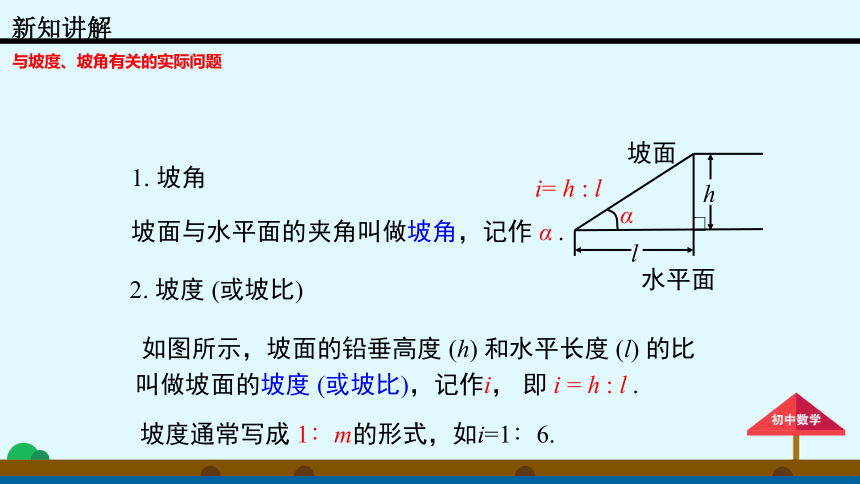
坡角
坡面与水平面的夹角叫做坡角,记作
α
.
2.
坡度
(或坡比)
坡度通常写成
1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度
(h)
和水平长度
(l)
的比叫做坡面的坡度
(或坡比),记作i,
即
i
=
h
:
l
.
坡面
水平面
与坡度、坡角有关的实际问题
新知讲解
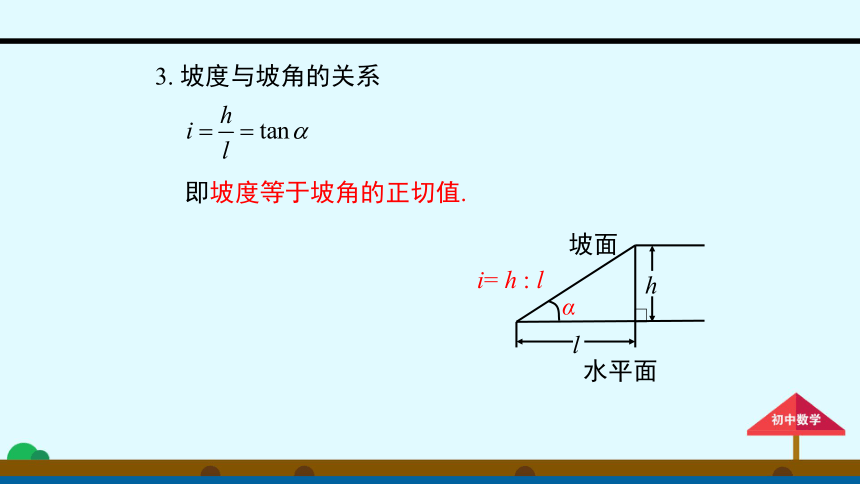
3.
坡度与坡角的关系
即坡度等于坡角的正切值.
α
l
h
i=
h
:
l
坡面
水平面
1.
斜坡的坡度是
,则坡角α
=___度.
2.
斜坡的坡角是45°
,则坡比是
_____.
3.
斜坡长是12米,坡高6米,则坡比是_______.
α
l
h
30
1
:
1
随堂演练
例1
如图,一山坡的坡度为i=1:2.小刚从山脚A出发,
沿山坡向上走了240m到达点C.这座山坡的坡角是多
少度?小刚上升了多少米(角度精确到0.01°,长
度精确到0.1m)?
i=1:2
典例精析
在Rt△ABC中,∠B=90°,∠A=26.57°,
AC=240m,
解:
用α表示坡角的大小,由题意可得
因此
α≈26.57°.
答:这座山坡的坡角约为26.57°,小刚上
升了约107.3
m.
从而
BC=240×sin26.57°≈107.3(m).
因此
例2
铁路路基的横断面是四边形ABCD,AD∥BC,路基宽BC=9.8m,高BE=5.8m,斜坡AB的坡度i=1∶1.6,斜坡CD的坡度i=1∶2.5,求:底宽AB和斜坡的坡角α和β
(精确到
1°);
A
D
B
C
i=1:2.5
5.8
9.8
α
i=1:1.6
解:
过C作CF⊥AD于点F,得
CF=BE,EF=BC,∠A=α,∠B=β.
β
F
∴AE=1.6×5.8=9.28(m),DF=2.5×5.8=14.5(m).
∴AD=AE+EF+DF=9.28+9.8+14.5≈33.6(m).
答:铁路路基下底宽为33.6m,斜坡的坡角分别为32°和21°
E
F
A
D
B
C
i=1:2.5
5.8
9.8
α
i=1:1.6
β
如图,小明周末上山踏青,他从山脚处的B点出发时,测得坡面AB的坡度为1
:
2,走
米到达山顶A处.这时,他发现山的另一坡面AC的最低点C的俯角是30°.请求出点B和点C的水平距离.
练一练
A
C
B
D
30°
答案:点B和点C的水平距离为
米.
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
h
h
α
α
l
l
合作探究
我们设法“化曲为直,以直代曲”.
我们可以把山坡“化整为零”地划分为一些小段,如图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角α1,这样就可以算出这段山坡的高度h1=l1sinα1.
h1
α1
l1
在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h.
以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容.
归纳总结
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l.
化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
x
y
o
Q1
Q2
R
P1(x1,y1)
α
α
P2(x2,y2)
例3:已知:在直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.
求证:
证明:由α是锐角,可知直线y=kx+b是上升的,即函数y=kx+b的值随x值的增大而增大.
如图,x1<x2,则y1<y2.过点P1,P2作x轴的垂线,垂足分别为Q1,Q2,
再过点P1作x轴的平行线P1R交P2Q2于点R,得
∠P2P1R=α.
在Rt△P2P1R中,
∵P1,P2都在直线y=kx+b上,
1.
如图,河坝横断面迎水坡AB的坡比是1
:
,坝高
BC=3m,则坡面AB的长度是
(
)
A.
9m
B.
6m
C.
m
D.
m
A
C
B
B
巩固练习
2.如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6
m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD的长(精确到0.1
m).
解:作DE⊥AB,
CF⊥AB,
垂足分别为E、F.
由题意可知
DE=CF=4
(米),CD=EF=12
(米).
4.
一段路基的横断面是梯形,高为4米,上底的宽是
12米,路基的坡面与地面的倾角分别是45°和30°,
求路基下底的宽
(精确到0.1米,
,
).
?
45°
30°
4米
12米
A
B
C
D
在Rt△ADE中,
E
F
在Rt△BCF中,同理可得
因此
AB=AE+EF+BF≈4+12+6.93≈22.93
(米).
答:
路基下底的宽约为22.93米.
(米).
(米).
45°
30°
4米
12米
A
B
C
D
E
F
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
本节小结
第23章
解直角三角形
沪科版数学九年级上册
第23章
解直角三角形
沪科版数学九年级上册
23.2
解直角三角形及其应用
第4课时
坡度问题及一次函数
k
的几何意义
1.理解并掌握坡度、坡比的定义;(重点)
2.学会用坡度、坡比解决实际问题.(难点)
学习目标
本节目标
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
A
B
C
引入新知
观察思考
α
l
h
i=
h
:
l
1.
坡角
坡面与水平面的夹角叫做坡角,记作
α
.
2.
坡度
(或坡比)
坡度通常写成
1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度
(h)
和水平长度
(l)
的比叫做坡面的坡度
(或坡比),记作i,
即
i
=
h
:
l
.
坡面
水平面
与坡度、坡角有关的实际问题
新知讲解
3.
坡度与坡角的关系
即坡度等于坡角的正切值.
α
l
h
i=
h
:
l
坡面
水平面
1.
斜坡的坡度是
,则坡角α
=___度.
2.
斜坡的坡角是45°
,则坡比是
_____.
3.
斜坡长是12米,坡高6米,则坡比是_______.
α
l
h
30
1
:
1
随堂演练
例1
如图,一山坡的坡度为i=1:2.小刚从山脚A出发,
沿山坡向上走了240m到达点C.这座山坡的坡角是多
少度?小刚上升了多少米(角度精确到0.01°,长
度精确到0.1m)?
i=1:2
典例精析
在Rt△ABC中,∠B=90°,∠A=26.57°,
AC=240m,
解:
用α表示坡角的大小,由题意可得
因此
α≈26.57°.
答:这座山坡的坡角约为26.57°,小刚上
升了约107.3
m.
从而
BC=240×sin26.57°≈107.3(m).
因此
例2
铁路路基的横断面是四边形ABCD,AD∥BC,路基宽BC=9.8m,高BE=5.8m,斜坡AB的坡度i=1∶1.6,斜坡CD的坡度i=1∶2.5,求:底宽AB和斜坡的坡角α和β
(精确到
1°);
A
D
B
C
i=1:2.5
5.8
9.8
α
i=1:1.6
解:
过C作CF⊥AD于点F,得
CF=BE,EF=BC,∠A=α,∠B=β.
β
F
∴AE=1.6×5.8=9.28(m),DF=2.5×5.8=14.5(m).
∴AD=AE+EF+DF=9.28+9.8+14.5≈33.6(m).
答:铁路路基下底宽为33.6m,斜坡的坡角分别为32°和21°
E
F
A
D
B
C
i=1:2.5
5.8
9.8
α
i=1:1.6
β
如图,小明周末上山踏青,他从山脚处的B点出发时,测得坡面AB的坡度为1
:
2,走
米到达山顶A处.这时,他发现山的另一坡面AC的最低点C的俯角是30°.请求出点B和点C的水平距离.
练一练
A
C
B
D
30°
答案:点B和点C的水平距离为
米.
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
h
h
α
α
l
l
合作探究
我们设法“化曲为直,以直代曲”.
我们可以把山坡“化整为零”地划分为一些小段,如图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角α1,这样就可以算出这段山坡的高度h1=l1sinα1.
h1
α1
l1
在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h.
以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容.
归纳总结
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l.
化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
x
y
o
Q1
Q2
R
P1(x1,y1)
α
α
P2(x2,y2)
例3:已知:在直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.
求证:
证明:由α是锐角,可知直线y=kx+b是上升的,即函数y=kx+b的值随x值的增大而增大.
如图,x1<x2,则y1<y2.过点P1,P2作x轴的垂线,垂足分别为Q1,Q2,
再过点P1作x轴的平行线P1R交P2Q2于点R,得
∠P2P1R=α.
在Rt△P2P1R中,
∵P1,P2都在直线y=kx+b上,
1.
如图,河坝横断面迎水坡AB的坡比是1
:
,坝高
BC=3m,则坡面AB的长度是
(
)
A.
9m
B.
6m
C.
m
D.
m
A
C
B
B
巩固练习
2.如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6
m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD的长(精确到0.1
m).
解:作DE⊥AB,
CF⊥AB,
垂足分别为E、F.
由题意可知
DE=CF=4
(米),CD=EF=12
(米).
4.
一段路基的横断面是梯形,高为4米,上底的宽是
12米,路基的坡面与地面的倾角分别是45°和30°,
求路基下底的宽
(精确到0.1米,
,
).
?
45°
30°
4米
12米
A
B
C
D
在Rt△ADE中,
E
F
在Rt△BCF中,同理可得
因此
AB=AE+EF+BF≈4+12+6.93≈22.93
(米).
答:
路基下底的宽约为22.93米.
(米).
(米).
45°
30°
4米
12米
A
B
C
D
E
F
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
本节小结
第23章
解直角三角形
沪科版数学九年级上册
