折叠、展开与从不同方向观察几何体
文档属性
| 名称 | 折叠、展开与从不同方向观察几何体 |

|
|
| 格式 | zip | ||
| 文件大小 | 77.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-17 00:00:00 | ||
图片预览

文档简介
初中数学导学案班级 姓名 发放时间 使用时间
学科 数学 编制人 朱全国 审核人 朱全国 教学案编号 4.1.1.2
课型 新课 课题 折叠、展开与从不同方向观察几何体
课标要求 能从不同方向看一些几何体,以及它们简单的组合得到的平面图形。初步培养学生的空间观念和几何直觉。了解直棱柱、圆柱、圆锥的展开图。能根据展开图想象相应的几何体。
重点难点 从不同角度观察几何体,了解直棱柱、圆柱、圆锥的展开图。探讨棱柱的顶点、棱数、面数之间的关系,巩固正方体11种展开图的画法,努力训练在展开图中找到相对的面。
教学过程设计 设计意图
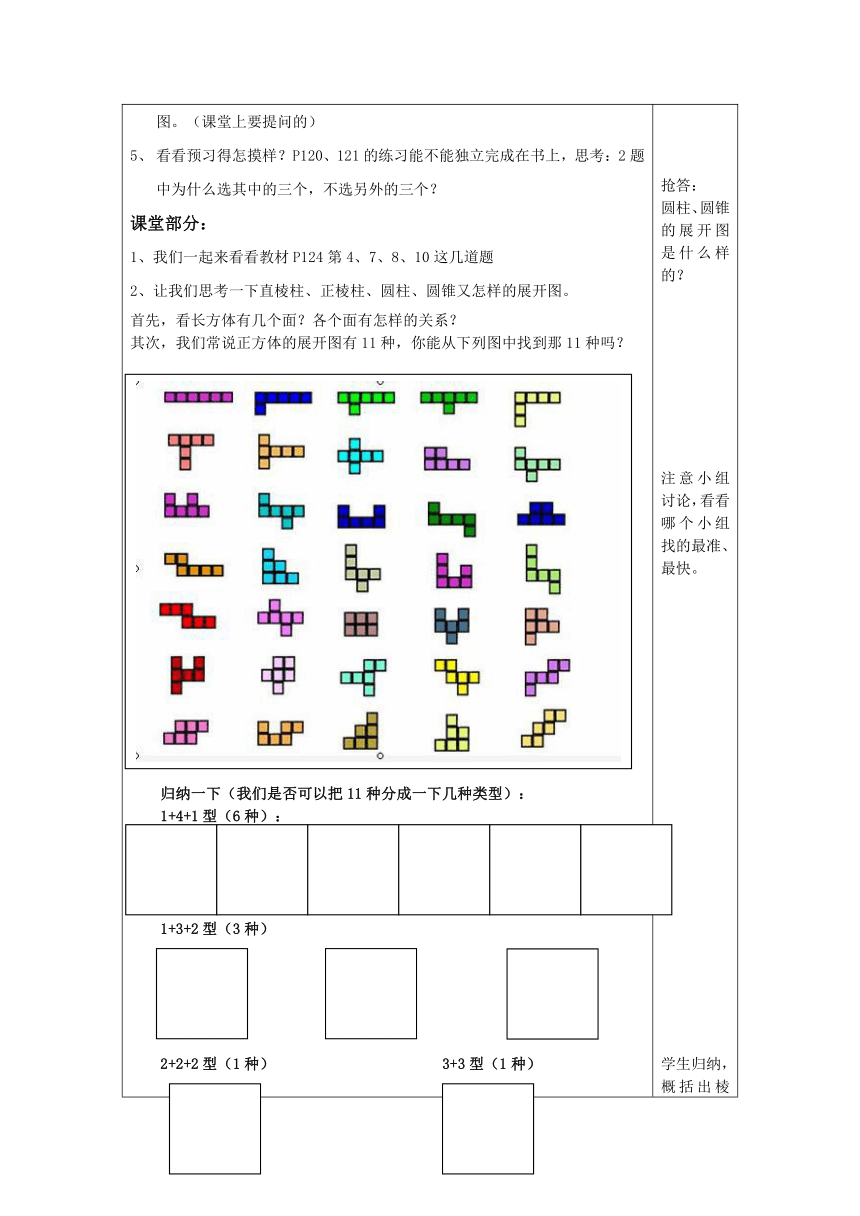
教材范围:P119--120学习目标:1、了解三视图,会画简单单个及多个规则几何体的三视图; 2、能将简单的立体图形的展开图折叠成立体图形,能将常见的柱体、椎体展开成平面图形;探讨棱柱的顶点、棱数、面数之间的关系。 3、巩固正方体11种展开图的画法,努力训练在展开图中找到相对的面。课前准备:一、预习关注:(一)要点感知:从 、 、 三个不同方向看立体图形,往往会得到不同形状的平面图形,我们称之为立体图形的三视图 ( http: / / www.21cnjy.com / " \t "_blank )。三视图就是主视图 ( http: / / www.21cnjy.com / " \t "_blank )(正视图)、俯视图 ( http: / / www.21cnjy.com / " \t "_blank )、左视图 ( http: / / www.21cnjy.com / " \t "_blank )(侧视图)的总称。(二)按一下要求预习并思考回答:结合要点感知独立阅读教材P119练习下面的内容。把P119的探究的结果展示在下面的方框内:独立阅读教材P119练习下面的内容。独立完成P120探究内容,并在书上写出各个展开图是什么几何体的展开图。(课堂上要提问的)看看预习得怎摸样?P120、121的练习能不能独立完成在书上,思考:2题中为什么选其中的三个,不选另外的三个?课堂部分:1、我们一起来看看教材P124第4、7、8、10这几道题2、让我们思考一下直棱柱、正棱柱、圆柱、圆锥又怎样的展开图。首先,看长方体有几个面?各个面有怎样的关系?其次,我们常说正方体的展开图有11种,你能从下列图中找到那11种吗?第3课时 几何图形的展开图归纳一下(我们是否可以把11种分成一下几种类型):1+4+1型(6种):1+3+2型(3种)2+2+2型(1种) 3+3型(1种)再次,我们思考一下正棱柱和直棱柱的联系与区别?联系: 区别:最后:我们练习一下在正方体的11种展开图中找到已知面(前字所在面)所对的面3、(1)现在我们来探索一下棱柱顶点、棱数、面数的关系,请同学们数一数常见棱柱的顶点数、棱数、面数。小组合作完成下面表格。看哪个组先完成。学生小组合作交流完成填表。棱 柱棱数顶点数面 数三棱柱四棱柱五棱柱六棱柱提出问题:同学们观察一下上面的数据,你能马上说出十棱柱的顶点数、棱数、面数吗?同学们小组商量一下。归纳一下,怎么才能又快又准的说出这三组数据我们的归纳为:发现n棱柱有 条棱, 个顶点, 个面。我们再看看这三组数据是不是始终存在一种关系:棱数=定点数 (填符号)面数 (填符号) (填数字)(2)用同样的方法探索一下棱锥顶点、棱数、面数的关系,请同学们数一数常见棱锥的顶点数、棱数、面数。小组合作完成下面表格。看哪个组先完成。学生小组合作交流完成填表。棱 锥棱数顶点数面 数三棱锥四棱锥五棱锥六棱锥提出问题:同学们观察一下上面的数据,你能马上说出十棱锥的顶点数、棱数、面数吗?同学们小组商量一下。归纳一下,怎么才能又快又准的说出这三组数据我们的归纳为:发现n棱锥有 条棱, 个顶点, 个面。我们再看看这三组数据是不是始终存在一种关系:棱数=定点数 (填符号)面数 (填符号) (填数字)最后我们总结无论棱柱还是棱锥它们的棱数、顶点数、面数始终满足:棱数=定点数 (填符号)面数 (填符号) (填数字)你来问问小组成员能不能很快速出一个任意棱柱或任意棱锥的棱数、顶点数、面数。4、我们来总结一下这节课学到了什么?课后作业:练习册P58、59,有一点提醒有种折叠问题课堂上我们没练到,看看你能不能大胆解决它们,老师相信你能行呀! 抢答:圆柱、圆锥的展开图是什么样的?注意小组讨论,看看哪个小组找的最准、最快。学生归纳,概括出棱柱的特性。棱柱上、下两个面形状、大小相同,棱柱侧棱相等,侧面是长方形,侧面的个数和底面图形的边数相等等。思考提示:需要你将静止的展开图“动起来”,我们可以让“前”字面做正方体最底下的面,然后想象折叠进而找到它相对的面。
正面看
上面看
左面看
理解记忆成:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。
学科 数学 编制人 朱全国 审核人 朱全国 教学案编号 4.1.1.2
课型 新课 课题 折叠、展开与从不同方向观察几何体
课标要求 能从不同方向看一些几何体,以及它们简单的组合得到的平面图形。初步培养学生的空间观念和几何直觉。了解直棱柱、圆柱、圆锥的展开图。能根据展开图想象相应的几何体。
重点难点 从不同角度观察几何体,了解直棱柱、圆柱、圆锥的展开图。探讨棱柱的顶点、棱数、面数之间的关系,巩固正方体11种展开图的画法,努力训练在展开图中找到相对的面。
教学过程设计 设计意图
教材范围:P119--120学习目标:1、了解三视图,会画简单单个及多个规则几何体的三视图; 2、能将简单的立体图形的展开图折叠成立体图形,能将常见的柱体、椎体展开成平面图形;探讨棱柱的顶点、棱数、面数之间的关系。 3、巩固正方体11种展开图的画法,努力训练在展开图中找到相对的面。课前准备:一、预习关注:(一)要点感知:从 、 、 三个不同方向看立体图形,往往会得到不同形状的平面图形,我们称之为立体图形的三视图 ( http: / / www.21cnjy.com / " \t "_blank )。三视图就是主视图 ( http: / / www.21cnjy.com / " \t "_blank )(正视图)、俯视图 ( http: / / www.21cnjy.com / " \t "_blank )、左视图 ( http: / / www.21cnjy.com / " \t "_blank )(侧视图)的总称。(二)按一下要求预习并思考回答:结合要点感知独立阅读教材P119练习下面的内容。把P119的探究的结果展示在下面的方框内:独立阅读教材P119练习下面的内容。独立完成P120探究内容,并在书上写出各个展开图是什么几何体的展开图。(课堂上要提问的)看看预习得怎摸样?P120、121的练习能不能独立完成在书上,思考:2题中为什么选其中的三个,不选另外的三个?课堂部分:1、我们一起来看看教材P124第4、7、8、10这几道题2、让我们思考一下直棱柱、正棱柱、圆柱、圆锥又怎样的展开图。首先,看长方体有几个面?各个面有怎样的关系?其次,我们常说正方体的展开图有11种,你能从下列图中找到那11种吗?第3课时 几何图形的展开图归纳一下(我们是否可以把11种分成一下几种类型):1+4+1型(6种):1+3+2型(3种)2+2+2型(1种) 3+3型(1种)再次,我们思考一下正棱柱和直棱柱的联系与区别?联系: 区别:最后:我们练习一下在正方体的11种展开图中找到已知面(前字所在面)所对的面3、(1)现在我们来探索一下棱柱顶点、棱数、面数的关系,请同学们数一数常见棱柱的顶点数、棱数、面数。小组合作完成下面表格。看哪个组先完成。学生小组合作交流完成填表。棱 柱棱数顶点数面 数三棱柱四棱柱五棱柱六棱柱提出问题:同学们观察一下上面的数据,你能马上说出十棱柱的顶点数、棱数、面数吗?同学们小组商量一下。归纳一下,怎么才能又快又准的说出这三组数据我们的归纳为:发现n棱柱有 条棱, 个顶点, 个面。我们再看看这三组数据是不是始终存在一种关系:棱数=定点数 (填符号)面数 (填符号) (填数字)(2)用同样的方法探索一下棱锥顶点、棱数、面数的关系,请同学们数一数常见棱锥的顶点数、棱数、面数。小组合作完成下面表格。看哪个组先完成。学生小组合作交流完成填表。棱 锥棱数顶点数面 数三棱锥四棱锥五棱锥六棱锥提出问题:同学们观察一下上面的数据,你能马上说出十棱锥的顶点数、棱数、面数吗?同学们小组商量一下。归纳一下,怎么才能又快又准的说出这三组数据我们的归纳为:发现n棱锥有 条棱, 个顶点, 个面。我们再看看这三组数据是不是始终存在一种关系:棱数=定点数 (填符号)面数 (填符号) (填数字)最后我们总结无论棱柱还是棱锥它们的棱数、顶点数、面数始终满足:棱数=定点数 (填符号)面数 (填符号) (填数字)你来问问小组成员能不能很快速出一个任意棱柱或任意棱锥的棱数、顶点数、面数。4、我们来总结一下这节课学到了什么?课后作业:练习册P58、59,有一点提醒有种折叠问题课堂上我们没练到,看看你能不能大胆解决它们,老师相信你能行呀! 抢答:圆柱、圆锥的展开图是什么样的?注意小组讨论,看看哪个小组找的最准、最快。学生归纳,概括出棱柱的特性。棱柱上、下两个面形状、大小相同,棱柱侧棱相等,侧面是长方形,侧面的个数和底面图形的边数相等等。思考提示:需要你将静止的展开图“动起来”,我们可以让“前”字面做正方体最底下的面,然后想象折叠进而找到它相对的面。
正面看
上面看
左面看
理解记忆成:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。
