高中物理必修二教案-6.5宇宙航行-人教版
文档属性
| 名称 | 高中物理必修二教案-6.5宇宙航行-人教版 | 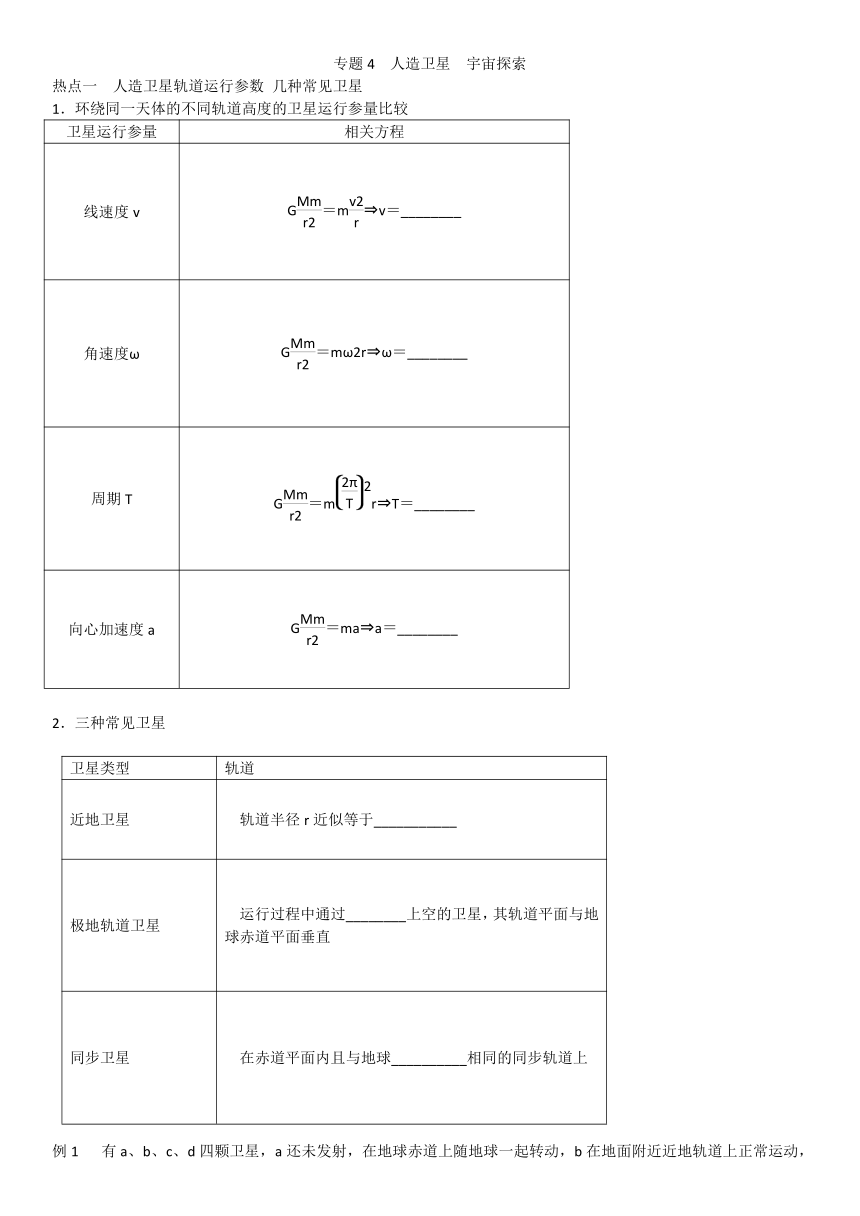 | |
| 格式 | docx | ||
| 文件大小 | 642.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-24 09:53:18 | ||
图片预览

文档简介
专题4 人造卫星 宇宙探索
热点一 人造卫星轨道运行参数 几种常见卫星
1.环绕同一天体的不同轨道高度的卫星运行参量比较
卫星运行参量
相关方程
线速度v
G=m?v=________
角速度ω
G=mω2r?ω=________
周期T
G=mr?T=________
向心加速度a
G=ma?a=________
2.三种常见卫星
卫星类型
轨道
近地卫星
轨道半径r近似等于___________
极地轨道卫星
运行过程中通过________上空的卫星,其轨道平面与地球赤道平面垂直
同步卫星
在赤道平面内且与地球__________相同的同步轨道上
例1 有a、b、c、d四颗卫星,a还未发射,在地球赤道上随地球一起转动,b在地面附近近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,设地球自转周期为24 h,所有卫星的运动均视为匀速圆周运动,各卫星排列位置如图Z41所示,则下列关于卫星的说法中正确的是( )
A.a的向心加速度等于重力加速度g
B.c在4 h内转过的圆心角为
C.b在相同的时间内转过的弧长最长
D.d的运动周期可能是23 h
变式题1 (近地卫星)已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,则航天器在火星表面附近绕火星做匀速圆周运动的速率约为( )
A.3.5 km/s
B.5.0 km/s
C.17.7 km/s
D.35.2 km/s
变式题2 (极地轨道卫星)[2016·河南郑州一中开学考试] 如图Z42所示,某极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道),若已知该卫星从地球上北纬30°的正上方,按图示方向第一次运行至南纬60°正上方时所用时间为t,地球半径为R(地球可看作均匀球体),地球表面的重力加速度为g,引力常量为G,由以上条件无法求出的物理量是( )
图Z42
A.卫星运动的周期
B.卫星所受的向心力
C.地球的质量
D.卫星距离地面的高度
变式题3 (同步卫星)研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时.假设这种趋势会持续下去,地球的其他条件都不变,未来人类发射的地球同步卫星与现在的相比( )
A.距地面的高度变大
B.向心加速度变大
C.线速度变大
D.角速度变大
热点二 人造卫星的变轨
卫星在轨期间改变运行轨道的过程称为变轨.其动力学本质为圆周运动需要的向心力与物体受到的万有引力大小变化的关系.
1.变轨原理及过程
人造卫星的发射过程要经过多次变轨方可到达预定轨道,如图Z43所示.
图Z43
(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上.
(2)在A点点火加速,由于速度变大,万有引力不足以提供向心力,卫星做离心运动进入椭圆轨道Ⅱ.
(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ.
2.三个运行物理量的大小比较
(1)速度:设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v1、v3,在轨道Ⅱ上过A点和B点速率分别为vA、vB.在A点加速,则vA>v1,在B点加速,则v3>vB,又因v1>v3,故有vA>v1>v3>vB.
(2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅱ上经过A点,卫星的加速度都相同,同理,经过B点加速度也相同.
(3)周期:设卫星在Ⅰ、Ⅱ、Ⅲ轨道上运行周期分别为T1、T2、T3,轨道半径分别为r1、r2(半长轴)、r3,由开普勒第三定律=k可知T1<T2<T3.
例2 (多选)发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1和2相切于Q点,轨道2和3相切于P点,设卫星在轨道1和轨道3正常运行的速度和加速度分别为v1、v3和a1、a3,在轨道2经过P点时的速度和加速度为v2和a2,且当卫星分别在1、2、3轨道上正常运行时周期分别为T1、T2 、T3,以下说法正确的是( )
图Z44
A.v1>v2>v3
B.v1>v3>v2
C.a1>a2>a3
D.T1<T2<T3
变式题1 (多选)(变轨中运行参量的比较)2013年12月2日,我国探月探测器“嫦娥三号”在西昌卫星发射中心成功发射升空,此飞行轨道示意图如图Z45所示,地面发射后奔向月球,在P点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,Q为轨道Ⅱ上的近月点.下列关于“嫦娥三号”的运动,正确的说法是( )
图Z45
A.发射速度一定大于7.9 km/s
B.在轨道Ⅱ上从P到Q的过程中速率不断增大
C.在轨道Ⅱ上经过P的速度小于在轨道Ⅰ上经过P的速度
D.在轨道Ⅱ上经过P的加速度小于在轨道Ⅰ上经过P的加速度
变式题2 (多选)(变轨中功能问题)[2014·山东卷] 2013年我国相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图Z46所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
falseA.(h+2R)
B.(h+R)
C.
D.
热点一 人造卫星轨道运行参数 几种常见卫星
1.环绕同一天体的不同轨道高度的卫星运行参量比较
卫星运行参量
相关方程
线速度v
G=m?v=________
角速度ω
G=mω2r?ω=________
周期T
G=mr?T=________
向心加速度a
G=ma?a=________
2.三种常见卫星
卫星类型
轨道
近地卫星
轨道半径r近似等于___________
极地轨道卫星
运行过程中通过________上空的卫星,其轨道平面与地球赤道平面垂直
同步卫星
在赤道平面内且与地球__________相同的同步轨道上
例1 有a、b、c、d四颗卫星,a还未发射,在地球赤道上随地球一起转动,b在地面附近近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,设地球自转周期为24 h,所有卫星的运动均视为匀速圆周运动,各卫星排列位置如图Z41所示,则下列关于卫星的说法中正确的是( )
A.a的向心加速度等于重力加速度g
B.c在4 h内转过的圆心角为
C.b在相同的时间内转过的弧长最长
D.d的运动周期可能是23 h
变式题1 (近地卫星)已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,则航天器在火星表面附近绕火星做匀速圆周运动的速率约为( )
A.3.5 km/s
B.5.0 km/s
C.17.7 km/s
D.35.2 km/s
变式题2 (极地轨道卫星)[2016·河南郑州一中开学考试] 如图Z42所示,某极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道),若已知该卫星从地球上北纬30°的正上方,按图示方向第一次运行至南纬60°正上方时所用时间为t,地球半径为R(地球可看作均匀球体),地球表面的重力加速度为g,引力常量为G,由以上条件无法求出的物理量是( )
图Z42
A.卫星运动的周期
B.卫星所受的向心力
C.地球的质量
D.卫星距离地面的高度
变式题3 (同步卫星)研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时.假设这种趋势会持续下去,地球的其他条件都不变,未来人类发射的地球同步卫星与现在的相比( )
A.距地面的高度变大
B.向心加速度变大
C.线速度变大
D.角速度变大
热点二 人造卫星的变轨
卫星在轨期间改变运行轨道的过程称为变轨.其动力学本质为圆周运动需要的向心力与物体受到的万有引力大小变化的关系.
1.变轨原理及过程
人造卫星的发射过程要经过多次变轨方可到达预定轨道,如图Z43所示.
图Z43
(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上.
(2)在A点点火加速,由于速度变大,万有引力不足以提供向心力,卫星做离心运动进入椭圆轨道Ⅱ.
(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ.
2.三个运行物理量的大小比较
(1)速度:设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v1、v3,在轨道Ⅱ上过A点和B点速率分别为vA、vB.在A点加速,则vA>v1,在B点加速,则v3>vB,又因v1>v3,故有vA>v1>v3>vB.
(2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅱ上经过A点,卫星的加速度都相同,同理,经过B点加速度也相同.
(3)周期:设卫星在Ⅰ、Ⅱ、Ⅲ轨道上运行周期分别为T1、T2、T3,轨道半径分别为r1、r2(半长轴)、r3,由开普勒第三定律=k可知T1<T2<T3.
例2 (多选)发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1和2相切于Q点,轨道2和3相切于P点,设卫星在轨道1和轨道3正常运行的速度和加速度分别为v1、v3和a1、a3,在轨道2经过P点时的速度和加速度为v2和a2,且当卫星分别在1、2、3轨道上正常运行时周期分别为T1、T2 、T3,以下说法正确的是( )
图Z44
A.v1>v2>v3
B.v1>v3>v2
C.a1>a2>a3
D.T1<T2<T3
变式题1 (多选)(变轨中运行参量的比较)2013年12月2日,我国探月探测器“嫦娥三号”在西昌卫星发射中心成功发射升空,此飞行轨道示意图如图Z45所示,地面发射后奔向月球,在P点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,Q为轨道Ⅱ上的近月点.下列关于“嫦娥三号”的运动,正确的说法是( )
图Z45
A.发射速度一定大于7.9 km/s
B.在轨道Ⅱ上从P到Q的过程中速率不断增大
C.在轨道Ⅱ上经过P的速度小于在轨道Ⅰ上经过P的速度
D.在轨道Ⅱ上经过P的加速度小于在轨道Ⅰ上经过P的加速度
变式题2 (多选)(变轨中功能问题)[2014·山东卷] 2013年我国相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图Z46所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
falseA.(h+2R)
B.(h+R)
C.
D.
