江苏省徐州市2020-2021学年高一上学期期中考试 数学 Word版含答案
文档属性
| 名称 | 江苏省徐州市2020-2021学年高一上学期期中考试 数学 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 502.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 20:47:53 | ||
图片预览



文档简介
2020~2021学年度第一学期期中考试
高一数学试题
考生在答题前请认真阅读本注意事项及各题答题要求
1.本试卷共4页,分为选择题(第1题到第12题)和非选择题(第13题到第22题)。本卷满分150分,考试时间为120分钟。考试结束后,请将答题纸交回。
2.答题前,请务必将自己的姓名、准考证号填写在答题纸规定的位置。
3.回答选择题时,选出每小题答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,必须用0.5毫米黑色签字笔将答案写在答题纸相应位置。在其它位置作答一律无效。
4.如需作图,须用2B铅笔绘图写清楚,线条符号等须加黑、加粗。
一、选择题:本大题共8小题,每小题5分,满分40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。请将选择题的答案填涂在答题卷上。
1.设集合A={1,2,4},B={2,3,4},则A∪B=
A.{2,4} B.{1,2,2,3,4} C.{1,2,3,4} D.{(1,2,3,4)}
2.函数y=的定义域
A.(-2,2) B.[-2,2] C.(-2,1)∪(1,2) D.[-2,1)∪(1,2]
3.设a∈R,则“a2>a”是“a<0”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知2x=3y=k,且=1,则k的值为
A.6 B. C.2 D.3
5.定义在R上的奇函数f(x)在(-∞,0)上单调递减,且f(3)=0,则满足xf(x+1)≥0的x的取值范围是
A.[-4,-1]∪[0,+∞) B.[-2,0]∪[1,4]
C.[-4,-1]∪[0,2] D.(-∞,-1]∪[0,2]
6.已知函数f(x)=ax2+2a是定义在[a,a+2]上的偶函数,又g(x)=f(x+1),则g(-),g(0),g(3)的大小关系为
A.g(0)>g(-)>g(3) B.g(-)>g(0)>g(3) C.g(0)>g(3)>g(-) D.g(3)>g(-)>g(0)
7.若x,y∈R+,3x+y=xy,则2x+y的最小值
A.2+5 B.4 C.12 D.6
8.对于集合A,B,若一个集合为另一个集合的子集时,则称这两个集合A,B之间构成“全食”;当集合A∩B≠,且互不为对方子集时,则称集合A、B之间构成“偏食”。对于集合A={-2,1,2},B={x|ax2=1,a≥0},若集合A,B构成“全食”或构成“偏食”,则a的取值集合为
A.{} B.{1,} C.{0,1,} D.{0,1,,}
二、选择题:本大题共4小题,每小题5分,满分20分。在每小题给出的四个选项中,有多项是符合题目要求的。全部选对的得5分,有选错的得0分,部分选对的得3分。
9.下列说法正确的有
A.若a>b,则ac2>bc2 B.若,则a>b C.若a>b,则 D.若a>b,则a3>b3
10.已知函数y=-x(x>1),则该函数
A.最大值为-3 B.最小值为1 C.没有最小值 D.最小值为-3
11.已知f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=-x2+2x,下列说法正确的是
A.x∈(0,+∞)时,函数解析式为f(x)=x2-2x B.函数在定义域R上为增函数
C.不等式f(3x-2)<3的解集为(-∞,1) D.不等式f(x)-x2+x-1>0恒成立
12.已知关于x的不等式ax2+bx+c>0,关于此不等式的解集有下列结论,其中正确的是
A.不等式ax2+bx+c>0的解集不可能是{x|x>6}
B.不等式ax2+bx+c>0的解集可以是R
C.不等式ax2+bx+c>0的解集可以是
D.不等式ax2+bx+c>0的解集可以是{x|2三、填空题:本大题共4小题,每小题5分,第16题第一空2分,第二空3分,共20分请将答案填在答题卷上。
13.已知集合A={4,2a+1,a},B={a-3,4-a,3}且A∩B={3},则a的取值为 。
14.已知y=f(x)是奇函数,当x>0时f(x)=,则f(-16)的值是 。
15.若命题“x∈R,使得ax2+ax-3≥0”是假命题,则实数a的取值范围为 。
16.定义:闭区间[a,b]的长度为b-a。已知二次函数f(x)=x2-2x+3,则不等式f(x)≤3解集的区间长度为 ,不等式f(x)≤m的解集的区间长度为8,则实数m的值是 。
四、解答题:本大题共6个小题,满分70份。解答须写出说明、证明过程和演算步骤。
17.(10分)计算下列各式的值:
(1);(2)。
18.(12分)已知集合A={x|<-1},B={x|(x-m-1)(x-m-7)>0}。
(1)若m=-2,求集合A∪B;
(2)若A∩B=,求实数m的取值范围。
19.(12分)已知集合A={x|y=},B={x|x2-2mx+m2-1≥0}。
(1)求集合A;
(2)若p:x∈A,q:x∈B,且p是q的充分不必要条件,求实数m的取值范围。
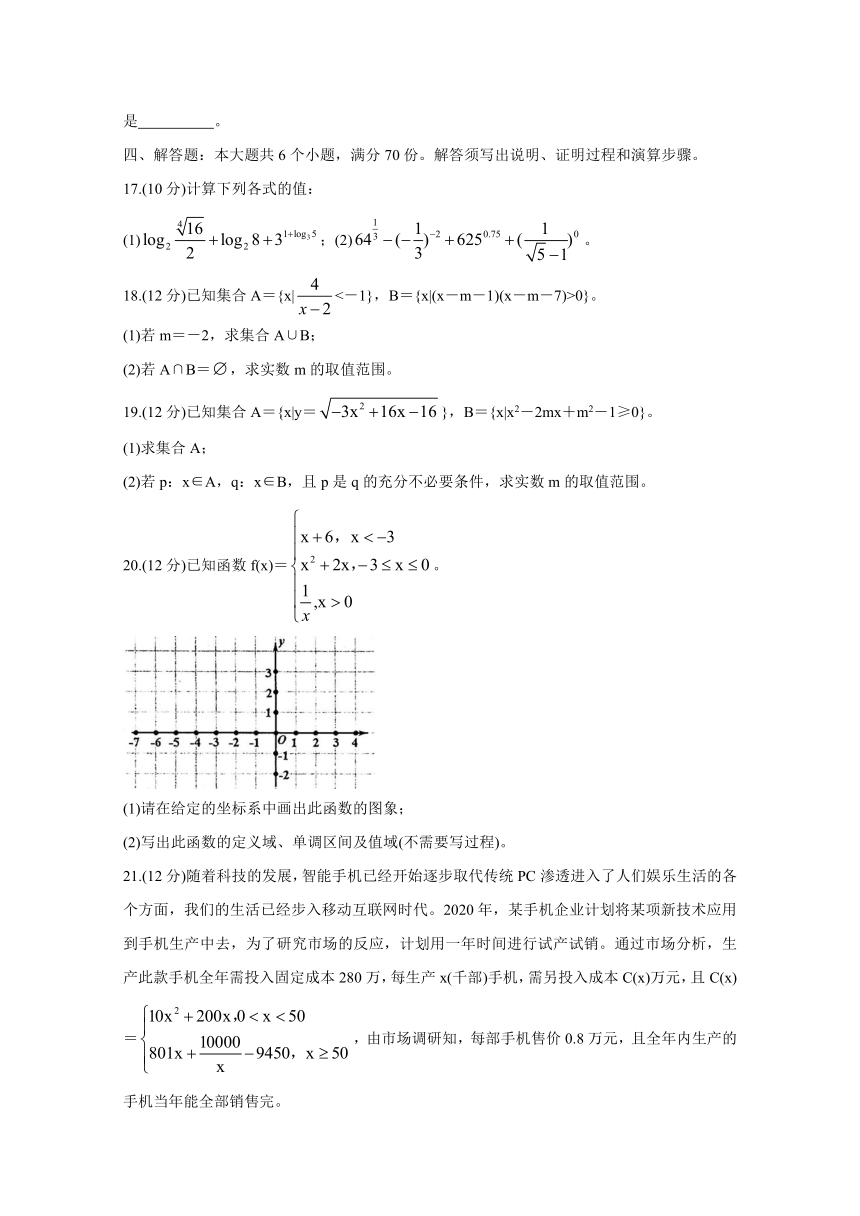
20.(12分)已知函数f(x)=。
(1)请在给定的坐标系中画出此函数的图象;
(2)写出此函数的定义域、单调区间及值域(不需要写过程)。
21.(12分)随着科技的发展,智能手机已经开始逐步取代传统PC渗透进入了人们娱乐生活的各个方面,我们的生活已经步入移动互联网时代。2020年,某手机企业计划将某项新技术应用到手机生产中去,为了研究市场的反应,计划用一年时间进行试产试销。通过市场分析,生产此款手机全年需投入固定成本280万,每生产x(千部)手机,需另投入成本C(x)万元,且C(x)=,由市场调研知,每部手机售价0.8万元,且全年内生产的手机当年能全部销售完。
(1)求出2020年的利润W(x)(万元)关于年产量x(千部)的函数关系式(利润=销售额-成本);
(2)2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
22.(12分)已知函数f(x)是定义在(-2,2)上的奇函数,满足f(1)=,当-2(1)求函数f(x)的解析式;
(2)判断f(x)的单调性,并利用定义证明;
(3)解不等式f(2x-1)+f(x)<0。
2020-2021学年度第一学期期中考试
高一数学试题
选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.请将选择题的答案填涂在答题卷上.
1. 2. 3. 4. 5. C 6. 7. 8.
二、选择题:本大题共4小题,每小题5分,满分20分.在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,有选错的得0分,部分选对的得3分.
9. 10. 11. 12.
三、填空题:本大题共4小题,每小题5分,第16题第一空2分,第二空3分,共20分.请将答案填在答题卷上.
13. 14. 15. 16. 2 18
四、解答题:本大题共6个小题,满分70份.解答须写出说明、证明过程和演算步骤.
17.解:(1)
…… 5分
(2)
…… 10分
18.解(1)由得,即, …… 2分
当时,由得, ……4分 ……6分
(2)由得,
即 ……………… 8分
因为,所以, ……………… 10分
即 ……………… 12分
19.解(1)∵
∴, ……………… 2分
则,∴,
∴. ……………… 4分
(2)∵
∴由可得,
∴ ……………… 6分
∵:,:,且是的充分不必要条件,
∴, ……………… 10分
∴,
∴实数的取值范围是. ……………… 12分
20.解 (1)略(图像完全作对才得分,否则0分) ………… 4分
(2)定义域, ……………… 6分
单调增区间和,
(写成闭也对,下同) ……………… 8分
单调减区间和, ……………… 10分
值域 ……………… 12分
21.解:(1)当时,
当时,,
……………… 2分
∴ ………………4分
(2)若,,当时,万元.
……………… 6分
若,,
当且仅当时,即时,万元. ……………… 8分
因为
所以2020年产量为100(千部)时,企业所获利润最大,最大利润是8970万元.………………11分
答(1)
(2)2020年产量为100(千部)时,企业所获利润最大,最大利润是8970万元.
………………12分
22.解:(1)函数是定义在上的奇函数
,即.
又因为,即,所以
经检验得符合题意.
综上所述,. ……………… 2分
(2),则
因为当时,有,函数是定义在上的奇函数
所以,
所以,
综上所述,. ……………… 4分
函数在为单调递增函数.证明如下:
任取,则
……… 6分
,,
,即,
故在上为增函数. ……………… 8分
(3)因为函数是定义在上的奇函数,
所以 ……………… 10分
由(2)知在上为增函数,
则解得,
所以,原不等式的解集为. ……………… 12分
高一数学试题
考生在答题前请认真阅读本注意事项及各题答题要求
1.本试卷共4页,分为选择题(第1题到第12题)和非选择题(第13题到第22题)。本卷满分150分,考试时间为120分钟。考试结束后,请将答题纸交回。
2.答题前,请务必将自己的姓名、准考证号填写在答题纸规定的位置。
3.回答选择题时,选出每小题答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,必须用0.5毫米黑色签字笔将答案写在答题纸相应位置。在其它位置作答一律无效。
4.如需作图,须用2B铅笔绘图写清楚,线条符号等须加黑、加粗。
一、选择题:本大题共8小题,每小题5分,满分40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。请将选择题的答案填涂在答题卷上。
1.设集合A={1,2,4},B={2,3,4},则A∪B=
A.{2,4} B.{1,2,2,3,4} C.{1,2,3,4} D.{(1,2,3,4)}
2.函数y=的定义域
A.(-2,2) B.[-2,2] C.(-2,1)∪(1,2) D.[-2,1)∪(1,2]
3.设a∈R,则“a2>a”是“a<0”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知2x=3y=k,且=1,则k的值为
A.6 B. C.2 D.3
5.定义在R上的奇函数f(x)在(-∞,0)上单调递减,且f(3)=0,则满足xf(x+1)≥0的x的取值范围是
A.[-4,-1]∪[0,+∞) B.[-2,0]∪[1,4]
C.[-4,-1]∪[0,2] D.(-∞,-1]∪[0,2]
6.已知函数f(x)=ax2+2a是定义在[a,a+2]上的偶函数,又g(x)=f(x+1),则g(-),g(0),g(3)的大小关系为
A.g(0)>g(-)>g(3) B.g(-)>g(0)>g(3) C.g(0)>g(3)>g(-) D.g(3)>g(-)>g(0)
7.若x,y∈R+,3x+y=xy,则2x+y的最小值
A.2+5 B.4 C.12 D.6
8.对于集合A,B,若一个集合为另一个集合的子集时,则称这两个集合A,B之间构成“全食”;当集合A∩B≠,且互不为对方子集时,则称集合A、B之间构成“偏食”。对于集合A={-2,1,2},B={x|ax2=1,a≥0},若集合A,B构成“全食”或构成“偏食”,则a的取值集合为
A.{} B.{1,} C.{0,1,} D.{0,1,,}
二、选择题:本大题共4小题,每小题5分,满分20分。在每小题给出的四个选项中,有多项是符合题目要求的。全部选对的得5分,有选错的得0分,部分选对的得3分。
9.下列说法正确的有
A.若a>b,则ac2>bc2 B.若,则a>b C.若a>b,则 D.若a>b,则a3>b3
10.已知函数y=-x(x>1),则该函数
A.最大值为-3 B.最小值为1 C.没有最小值 D.最小值为-3
11.已知f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=-x2+2x,下列说法正确的是
A.x∈(0,+∞)时,函数解析式为f(x)=x2-2x B.函数在定义域R上为增函数
C.不等式f(3x-2)<3的解集为(-∞,1) D.不等式f(x)-x2+x-1>0恒成立
12.已知关于x的不等式ax2+bx+c>0,关于此不等式的解集有下列结论,其中正确的是
A.不等式ax2+bx+c>0的解集不可能是{x|x>6}
B.不等式ax2+bx+c>0的解集可以是R
C.不等式ax2+bx+c>0的解集可以是
D.不等式ax2+bx+c>0的解集可以是{x|2
13.已知集合A={4,2a+1,a},B={a-3,4-a,3}且A∩B={3},则a的取值为 。
14.已知y=f(x)是奇函数,当x>0时f(x)=,则f(-16)的值是 。
15.若命题“x∈R,使得ax2+ax-3≥0”是假命题,则实数a的取值范围为 。
16.定义:闭区间[a,b]的长度为b-a。已知二次函数f(x)=x2-2x+3,则不等式f(x)≤3解集的区间长度为 ,不等式f(x)≤m的解集的区间长度为8,则实数m的值是 。
四、解答题:本大题共6个小题,满分70份。解答须写出说明、证明过程和演算步骤。
17.(10分)计算下列各式的值:
(1);(2)。
18.(12分)已知集合A={x|<-1},B={x|(x-m-1)(x-m-7)>0}。
(1)若m=-2,求集合A∪B;
(2)若A∩B=,求实数m的取值范围。
19.(12分)已知集合A={x|y=},B={x|x2-2mx+m2-1≥0}。
(1)求集合A;
(2)若p:x∈A,q:x∈B,且p是q的充分不必要条件,求实数m的取值范围。
20.(12分)已知函数f(x)=。
(1)请在给定的坐标系中画出此函数的图象;
(2)写出此函数的定义域、单调区间及值域(不需要写过程)。
21.(12分)随着科技的发展,智能手机已经开始逐步取代传统PC渗透进入了人们娱乐生活的各个方面,我们的生活已经步入移动互联网时代。2020年,某手机企业计划将某项新技术应用到手机生产中去,为了研究市场的反应,计划用一年时间进行试产试销。通过市场分析,生产此款手机全年需投入固定成本280万,每生产x(千部)手机,需另投入成本C(x)万元,且C(x)=,由市场调研知,每部手机售价0.8万元,且全年内生产的手机当年能全部销售完。
(1)求出2020年的利润W(x)(万元)关于年产量x(千部)的函数关系式(利润=销售额-成本);
(2)2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
22.(12分)已知函数f(x)是定义在(-2,2)上的奇函数,满足f(1)=,当-2
(2)判断f(x)的单调性,并利用定义证明;
(3)解不等式f(2x-1)+f(x)<0。
2020-2021学年度第一学期期中考试
高一数学试题
选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.请将选择题的答案填涂在答题卷上.
1. 2. 3. 4. 5. C 6. 7. 8.
二、选择题:本大题共4小题,每小题5分,满分20分.在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,有选错的得0分,部分选对的得3分.
9. 10. 11. 12.
三、填空题:本大题共4小题,每小题5分,第16题第一空2分,第二空3分,共20分.请将答案填在答题卷上.
13. 14. 15. 16. 2 18
四、解答题:本大题共6个小题,满分70份.解答须写出说明、证明过程和演算步骤.
17.解:(1)
…… 5分
(2)
…… 10分
18.解(1)由得,即, …… 2分
当时,由得, ……4分 ……6分
(2)由得,
即 ……………… 8分
因为,所以, ……………… 10分
即 ……………… 12分
19.解(1)∵
∴, ……………… 2分
则,∴,
∴. ……………… 4分
(2)∵
∴由可得,
∴ ……………… 6分
∵:,:,且是的充分不必要条件,
∴, ……………… 10分
∴,
∴实数的取值范围是. ……………… 12分
20.解 (1)略(图像完全作对才得分,否则0分) ………… 4分
(2)定义域, ……………… 6分
单调增区间和,
(写成闭也对,下同) ……………… 8分
单调减区间和, ……………… 10分
值域 ……………… 12分
21.解:(1)当时,
当时,,
……………… 2分
∴ ………………4分
(2)若,,当时,万元.
……………… 6分
若,,
当且仅当时,即时,万元. ……………… 8分
因为
所以2020年产量为100(千部)时,企业所获利润最大,最大利润是8970万元.………………11分
答(1)
(2)2020年产量为100(千部)时,企业所获利润最大,最大利润是8970万元.
………………12分
22.解:(1)函数是定义在上的奇函数
,即.
又因为,即,所以
经检验得符合题意.
综上所述,. ……………… 2分
(2),则
因为当时,有,函数是定义在上的奇函数
所以,
所以,
综上所述,. ……………… 4分
函数在为单调递增函数.证明如下:
任取,则
……… 6分
,,
,即,
故在上为增函数. ……………… 8分
(3)因为函数是定义在上的奇函数,
所以 ……………… 10分
由(2)知在上为增函数,
则解得,
所以,原不等式的解集为. ……………… 12分
同课章节目录
