1.1.2余弦定理-人教A版高中数学必修五课件(28张PPT)
文档属性
| 名称 | 1.1.2余弦定理-人教A版高中数学必修五课件(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 716.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览




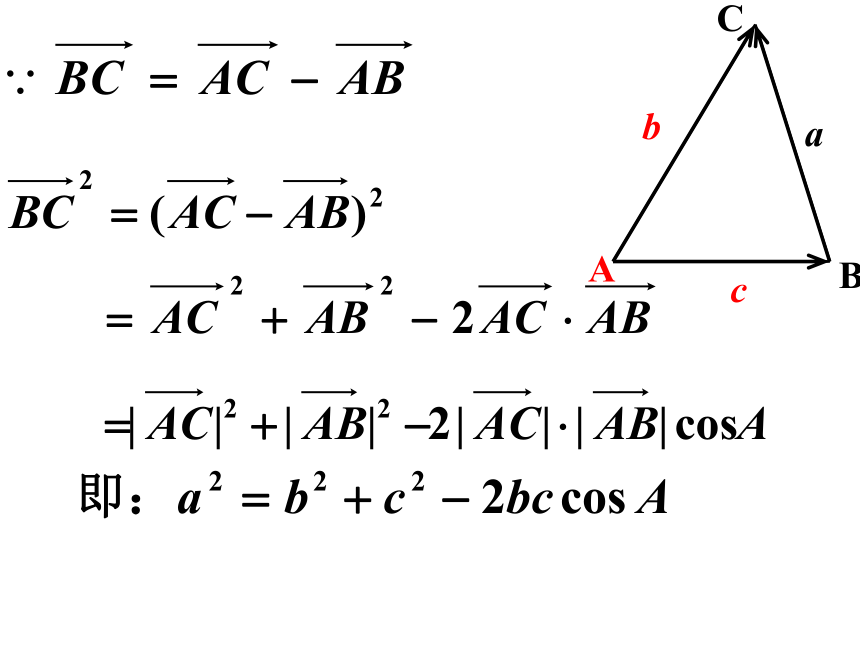



文档简介
1.1.2余弦定理
一、复习回顾:
1.正弦定理的形式是什么?
2.正弦定理解决了解三角形的哪些类型?
A
B
C
c
a
b
(1)已知两角和任一边
(2)已知两边和一边的对角
2、若A,B,C是△ABC的三个内角,则sinA+sinB____sinC.(大小关系)
>
B
回顾练习
1、在△ABC中,一定成立的等式是( )
A. asinA=bsinB B. acosA=bcosB
C. asinB=bsinA D. acosB=bcosA
C
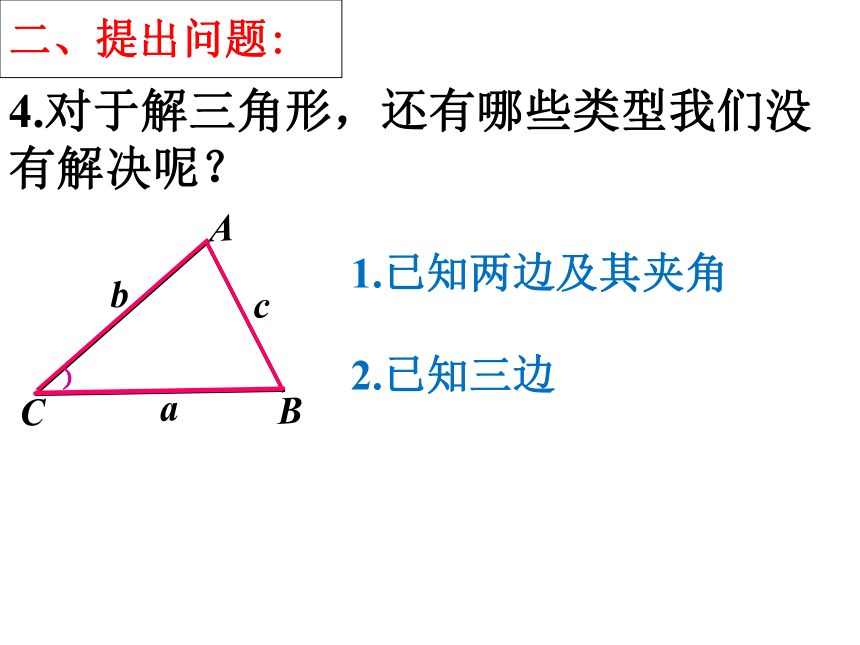
二、提出问题:
4.对于解三角形,还有哪些类型我们没有解决呢?
A
B
C
c
a
b
1.已知两边及其夹角
﹚
2.已知三边
探究:如何从已知的两边和它们的夹角计算出三角形的其他元素?
研究:如图在△ABC中,设AB=c,BC=a,CA=b,已知:b,c和A.求a
A
B
c
C
b
a
A
B
c
C
b
a
由此可得:余弦定理
三角形任一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
应用:已知两边和一个夹角,求第三边.
三、例题
巩固练习:在△ABC中,
(1)已知b=8,c=3,A=60°,则a=_______
(2)已知a=7,b=8,cosC= ,则c=_______
(3)已知a=5,c=7,tanB= , 则b=_______
7
3
余弦定理的推论:
应用:已知三条边求角度.
例2、在△ABC中,已知a=7,b=3,c=8,求角A.
例3、在△ABC中,a2>b2+c2,那么A是( )
A、钝角 B、直角
C、锐角 D、不能确定
A
(1)A为直角?a?=b?+c?
(2)A为锐角?a?(3)A为钝角?a?>b?+c?
结论:一般地,判断△ABC是锐角,直角还是钝角三角形,可用如下方法.
设a是最长边,则由 可得
试一试
若三角形的三边为7,8,3,试判断此三角形的形状.
钝角三角形
四.小结
四类解三角形问题:
(1)已知两角和任意一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求其他的边和角。
(3)已知两边和它们的夹角,求第三边和其他两个角;
(4)已知三边,求三个角。
五、题型探究
题型一 余弦定理的简单应用
例1、设△ABC的内角A,B,C所对的边分别为a,b,c,若(a+b-c)(a+b+c)=ab,则角C= .?
变式练习:
1、在△ABC中,B=60°,那么a2-ac+c2-b2=_
2、已知在△ABC中,a2=b2+c2+bc,求A的值.
题型二 利用余弦定理判断三角形形状
例2、在△ABC中,已知c=acosB,b=asinC,试判断△ABC的形状.
练习2、在△ABC中,已知(a+b+c)(a+b-c)=3ab,且2cos Asin B=sin C,试确定△ABC的形状.
法一,利用边的关系来判定
法二,利用角的关系来判定
练习3、在△ABC中,a,b,c分别表示三个内角A,B,C的对边,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),试判断该三角形的形状.
解:法一:∵(a2+b2)sin(A-B)=(a2-b2)·sin(A+B),
化简得,2a2cosAsinB=2b2cosBsinA.
∴正弦定理得sin2AcosAsinB=sin2BcosBsinA,
即sin2AsinAsinB=sin2BsinAsinB.
∵0∴2A=2B或2A=π-2B,即A=B或A+B=
∴△ABC是等腰三角形或直角三角形.
题型三 正、余弦定理综合
六、练习
3、设△ABC的内角A、B、C所对边的长分别为a、b、c,且有2sinBcosA=sinAcosC+cosAsinC.
(1)求角A的大小;
(2)若b=2,c=1,D为BC的中点,求AD的长.
4、在△ABC中,a=7,b=3,c=5,求最大角和sinC.
5、等腰三角形的底边长为a,腰长为2a,求腰上的中线长。
6、已知一钝角三角形的边长是三个连续自然数,求该三角形的三边长。
7、若三角形的三个角的比是1:2:3,最大的边20,则最小的边是_____.
参考答案
4、10.
一、复习回顾:
1.正弦定理的形式是什么?
2.正弦定理解决了解三角形的哪些类型?
A
B
C
c
a
b
(1)已知两角和任一边
(2)已知两边和一边的对角
2、若A,B,C是△ABC的三个内角,则sinA+sinB____sinC.(大小关系)
>
B
回顾练习
1、在△ABC中,一定成立的等式是( )
A. asinA=bsinB B. acosA=bcosB
C. asinB=bsinA D. acosB=bcosA
C
二、提出问题:
4.对于解三角形,还有哪些类型我们没有解决呢?
A
B
C
c
a
b
1.已知两边及其夹角
﹚
2.已知三边
探究:如何从已知的两边和它们的夹角计算出三角形的其他元素?
研究:如图在△ABC中,设AB=c,BC=a,CA=b,已知:b,c和A.求a
A
B
c
C
b
a
A
B
c
C
b
a
由此可得:余弦定理
三角形任一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
应用:已知两边和一个夹角,求第三边.
三、例题
巩固练习:在△ABC中,
(1)已知b=8,c=3,A=60°,则a=_______
(2)已知a=7,b=8,cosC= ,则c=_______
(3)已知a=5,c=7,tanB= , 则b=_______
7
3
余弦定理的推论:
应用:已知三条边求角度.
例2、在△ABC中,已知a=7,b=3,c=8,求角A.
例3、在△ABC中,a2>b2+c2,那么A是( )
A、钝角 B、直角
C、锐角 D、不能确定
A
(1)A为直角?a?=b?+c?
(2)A为锐角?a?
结论:一般地,判断△ABC是锐角,直角还是钝角三角形,可用如下方法.
设a是最长边,则由 可得
试一试
若三角形的三边为7,8,3,试判断此三角形的形状.
钝角三角形
四.小结
四类解三角形问题:
(1)已知两角和任意一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求其他的边和角。
(3)已知两边和它们的夹角,求第三边和其他两个角;
(4)已知三边,求三个角。
五、题型探究
题型一 余弦定理的简单应用
例1、设△ABC的内角A,B,C所对的边分别为a,b,c,若(a+b-c)(a+b+c)=ab,则角C= .?
变式练习:
1、在△ABC中,B=60°,那么a2-ac+c2-b2=_
2、已知在△ABC中,a2=b2+c2+bc,求A的值.
题型二 利用余弦定理判断三角形形状
例2、在△ABC中,已知c=acosB,b=asinC,试判断△ABC的形状.
练习2、在△ABC中,已知(a+b+c)(a+b-c)=3ab,且2cos Asin B=sin C,试确定△ABC的形状.
法一,利用边的关系来判定
法二,利用角的关系来判定
练习3、在△ABC中,a,b,c分别表示三个内角A,B,C的对边,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),试判断该三角形的形状.
解:法一:∵(a2+b2)sin(A-B)=(a2-b2)·sin(A+B),
化简得,2a2cosAsinB=2b2cosBsinA.
∴正弦定理得sin2AcosAsinB=sin2BcosBsinA,
即sin2AsinAsinB=sin2BsinAsinB.
∵0
∴△ABC是等腰三角形或直角三角形.
题型三 正、余弦定理综合
六、练习
3、设△ABC的内角A、B、C所对边的长分别为a、b、c,且有2sinBcosA=sinAcosC+cosAsinC.
(1)求角A的大小;
(2)若b=2,c=1,D为BC的中点,求AD的长.
4、在△ABC中,a=7,b=3,c=5,求最大角和sinC.
5、等腰三角形的底边长为a,腰长为2a,求腰上的中线长。
6、已知一钝角三角形的边长是三个连续自然数,求该三角形的三边长。
7、若三角形的三个角的比是1:2:3,最大的边20,则最小的边是_____.
参考答案
4、10.
