1.2充分条件与必要条件-人教A版高中数学选修2-1课件(21张PPT)
文档属性
| 名称 | 1.2充分条件与必要条件-人教A版高中数学选修2-1课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 524.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 22:55:23 | ||
图片预览








文档简介
第一章 1.2充分条件与必要条件
1.2 充分条件与必要条件
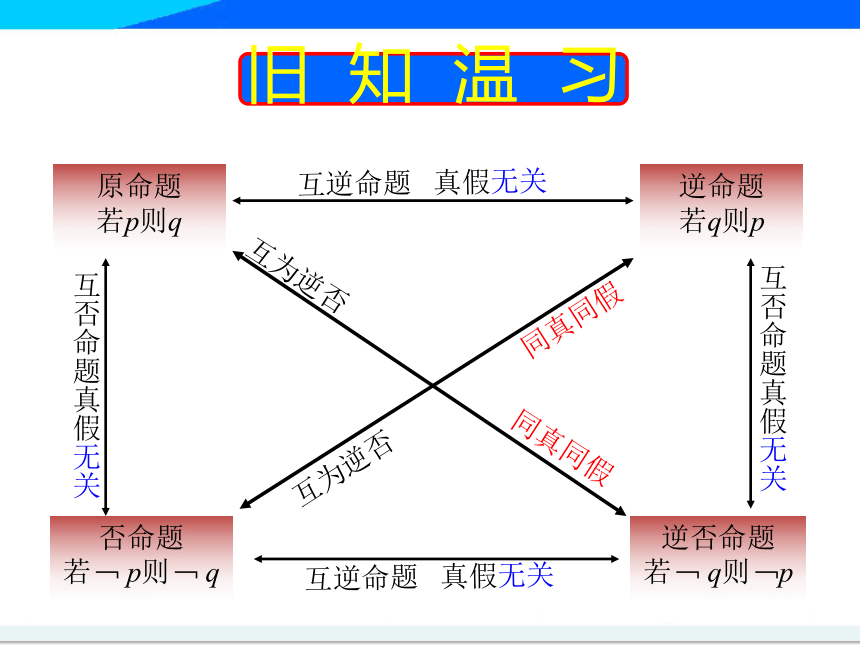
旧知温习
原命题
若p则q
逆命题
若q则p
否命题
若﹁ p则﹁ q
逆否命题
若﹁ q则﹁p
互为逆否 同真同假
互为逆否 同真同假
互逆命题 真假无关
互逆命题 真假无关
互否命题真假无关
互否命题真假无关
课堂导入
情境一:
如果同学甲是我校高二年级的学生,那么该生一定是我校学生吗?
反之,若同学甲是我校学生,则他一定是我校高二年级学生吗?
p是q的充分条件
q是p的必要条件
则称:
新课讲解
p:同学甲是我校高二学生
举例
q:同学甲是我校学生
p是q的充分条件
q是p的必要条件
p:全班都准时到校
q:班长没有迟到
p:张三是音乐老师
q:张三是老师
充分条件的含义用通俗语言来说是指“有它就行”
必要条件的含义用通俗语言来说是指“缺它不行”
定义:如果命题“若p,则q”为真命题,即p ? q, 那么我们就说p是q的充分条件;q是p的必要条件.
【定义得出】
①充分性:条件是充分的,也就是说条件是充足的,足够的,足以保证的。符合“若p则q”为真(p=>q)的形式,即“有之必成立”。
②必要性:必要就是必须的,必不可少的。符合“若非q则非p” 为真(非q=>非p)的形式,即“无之必不成立”。
注:
③p是q的充分条件与q是p的必要条件是完全等价的,它们是同一个逻辑关系“p=>q”的不同表达方法。
概念理解
注:
箭头所指为必要,箭尾所指为充分。
概念理解
解:上述三个命题都是真命题,所以 都是 的充分条件.
问题:
对于以上命题,我们可不可以称 是 的必要条件呢?
概念理解
概念理解
新知体会
小结:例1、练习1、练习2
例2、用“充分条件”或“必要条件”填空:
(1)a>5是a>0的______________;
(2)四边形的对角线互相垂直是四边形为菱形的___________.
必要条件
充分条件
知识应用
自主建构
知识联系
A
B
A、B
历史文化
A
B
A、B
充分条件:有之则必然,无之则未必不然;
必要条件:无之则必不然,有之则未必然 。
我国战国时期,墨子所著《墨经》
理性认识
注:小范围推出大范围。
知识应用
M
N
分析:(1)
(2)
知识应用
思考:
将(1)、(2)中“充分条件”改为“必要条件“,结果又会怎样?
解:(1)由题意得, ,
(2)由题意得, ,
练练手
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
课堂小结
1、充分条件与必要条件的概念;
2、充分条件与必要条件的判断;
总结提高
3、充分条件和必要条件与集合之间的联系.
学会观察、归纳、总结,进行探索发现,注意逻辑推理的合理性和严密性.
一、知识内容:
二、过程方法:
墨子 战国初期思想家,墨家学派创始人。
1.2 充分条件与必要条件
旧知温习
原命题
若p则q
逆命题
若q则p
否命题
若﹁ p则﹁ q
逆否命题
若﹁ q则﹁p
互为逆否 同真同假
互为逆否 同真同假
互逆命题 真假无关
互逆命题 真假无关
互否命题真假无关
互否命题真假无关
课堂导入
情境一:
如果同学甲是我校高二年级的学生,那么该生一定是我校学生吗?
反之,若同学甲是我校学生,则他一定是我校高二年级学生吗?
p是q的充分条件
q是p的必要条件
则称:
新课讲解
p:同学甲是我校高二学生
举例
q:同学甲是我校学生
p是q的充分条件
q是p的必要条件
p:全班都准时到校
q:班长没有迟到
p:张三是音乐老师
q:张三是老师
充分条件的含义用通俗语言来说是指“有它就行”
必要条件的含义用通俗语言来说是指“缺它不行”
定义:如果命题“若p,则q”为真命题,即p ? q, 那么我们就说p是q的充分条件;q是p的必要条件.
【定义得出】
①充分性:条件是充分的,也就是说条件是充足的,足够的,足以保证的。符合“若p则q”为真(p=>q)的形式,即“有之必成立”。
②必要性:必要就是必须的,必不可少的。符合“若非q则非p” 为真(非q=>非p)的形式,即“无之必不成立”。
注:
③p是q的充分条件与q是p的必要条件是完全等价的,它们是同一个逻辑关系“p=>q”的不同表达方法。
概念理解
注:
箭头所指为必要,箭尾所指为充分。
概念理解
解:上述三个命题都是真命题,所以 都是 的充分条件.
问题:
对于以上命题,我们可不可以称 是 的必要条件呢?
概念理解
概念理解
新知体会
小结:例1、练习1、练习2
例2、用“充分条件”或“必要条件”填空:
(1)a>5是a>0的______________;
(2)四边形的对角线互相垂直是四边形为菱形的___________.
必要条件
充分条件
知识应用
自主建构
知识联系
A
B
A、B
历史文化
A
B
A、B
充分条件:有之则必然,无之则未必不然;
必要条件:无之则必不然,有之则未必然 。
我国战国时期,墨子所著《墨经》
理性认识
注:小范围推出大范围。
知识应用
M
N
分析:(1)
(2)
知识应用
思考:
将(1)、(2)中“充分条件”改为“必要条件“,结果又会怎样?
解:(1)由题意得, ,
(2)由题意得, ,
练练手
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
课堂小结
1、充分条件与必要条件的概念;
2、充分条件与必要条件的判断;
总结提高
3、充分条件和必要条件与集合之间的联系.
学会观察、归纳、总结,进行探索发现,注意逻辑推理的合理性和严密性.
一、知识内容:
二、过程方法:
墨子 战国初期思想家,墨家学派创始人。
