1.2解三角形应用举例1-人教A版高中数学必修五课件(14张PPT)
文档属性
| 名称 | 1.2解三角形应用举例1-人教A版高中数学必修五课件(14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 659.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 22:56:25 | ||
图片预览





文档简介
1.2 应用举例
第一课时 正、余弦定理在实际中的应用
解三角形中的有关名词、术语:
(1)坡度:斜面与地平面所成的角度。
(2)仰角和俯角:在视线和水平线所成的角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
(3)方位角:从正北方向顺时针转到目标方向的夹角。
(4)视角:由物体两端射出的两条光线在眼球内交叉而成的角
(5)基线:在测量上,我们根据测量需要适当确定的线段叫做基线.一般来说,基线越长,测量的精确度越高.
题型一 测量距离问题
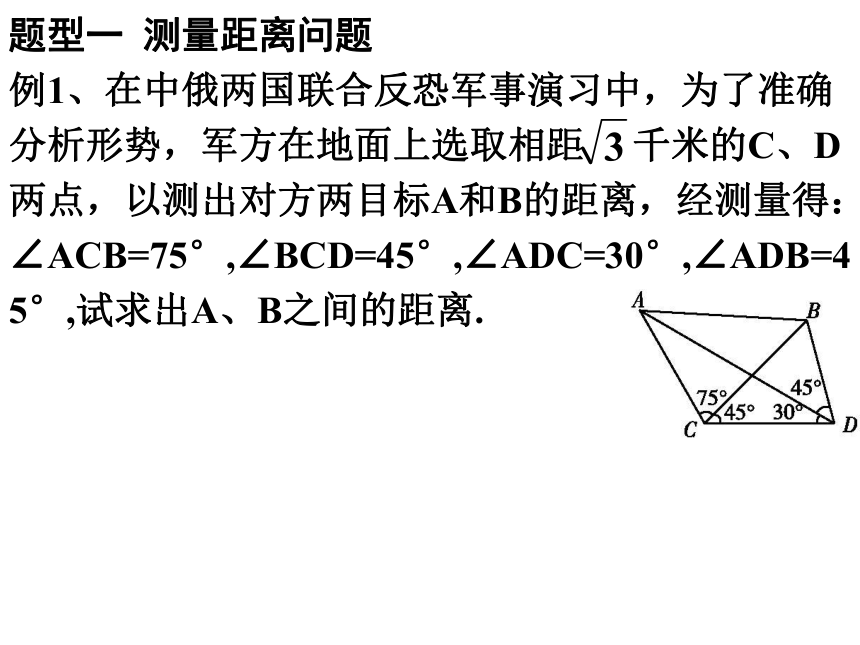
例1、在中俄两国联合反恐军事演习中,为了准确分析形势,军方在地面上选取相距 千米的C、D两点,以测出对方两目标A和B的距离,经测量得:∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,试求出A、B之间的距离.
跟踪训练1:
如图所示,为了计算湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测AD⊥CD,AD=5km, AB=7km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离.(假设A,B,C,D在同一平面内)
题型二 测量高度问题
例2、如图,为了测量河对岸的塔高AB,有不同的方案,其中之一是选取与塔底B在同一水平面内的两个测点C和D,测得CD=200米,在C点和D点测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.
跟踪训练2:
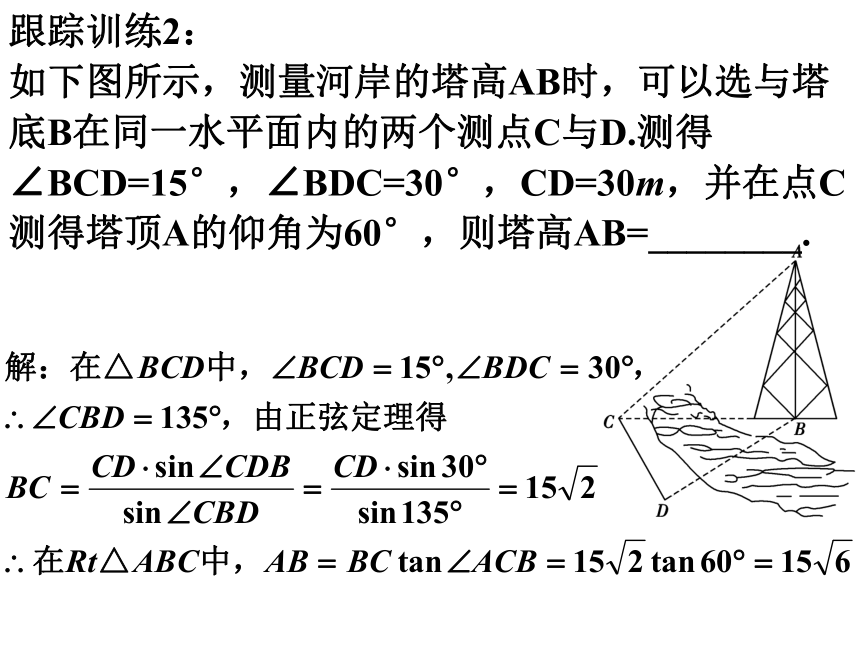
如下图所示,测量河岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C测得塔顶A的仰角为60°,则塔高AB=________.
题型三 测量角度问题
例3、某海上养殖基地A,接到气象部门预报,位于基地南偏东60°相距 海里的海面上有一台风中心,影响半径为20海里,正以每小时 海里的速度沿某一方向匀速直线前进,预计台风中心将从基地东北方向刮过且 小时后开始影响基地持续2小时,求台风移动的方向.
南
D
C
B
A
60°
解:如图所示,设预报时台风中心为B,开始影响基地时台风中心为C,基地刚好不受影响时台风中心为D,
则B、C、D在一条直线上,且AD=20、AC=20.
跟踪训练3:在海岸A处发现北偏东45°距离A处 海里的B处有一艘走私船,在A处北偏西75°的方向,距离A处2海里的C处的缉私船奉命以 海里/小时的速度追截走私船.此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船什么方向能最快追上走私船?
解:如图若要最快追上走私船,则两船到D点时所用时间相等.
假设在D处相遇,设缉私船用t h在D处追上走私船,如图.
则有CD= ,BD=10t
题型三 测量角度问题
例3、在某点B处测得建筑物AE的顶端A的仰角为q,沿BE方向前进30m,至点C处测得顶端A的仰角为2q,再继续前进 至D点,测得顶端A的仰角为4q,求q的大小和建筑物AE的高.
A
B
C
D
E
课后练习
1、在相距2km的A、B两点处测量目标点C,若∠CAB=750, ∠CBA=600,则A、C两点之间的距离是______km.
2、在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( )
A
3、一艘船以32n mile / h的速度向正北航行。在A处看灯塔S在船的北偏东45o的方向,30min后航行到B处,在B处看灯塔在船的北偏东75o的方向,已知距离此灯塔20n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
450
750
第一课时 正、余弦定理在实际中的应用
解三角形中的有关名词、术语:
(1)坡度:斜面与地平面所成的角度。
(2)仰角和俯角:在视线和水平线所成的角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
(3)方位角:从正北方向顺时针转到目标方向的夹角。
(4)视角:由物体两端射出的两条光线在眼球内交叉而成的角
(5)基线:在测量上,我们根据测量需要适当确定的线段叫做基线.一般来说,基线越长,测量的精确度越高.
题型一 测量距离问题
例1、在中俄两国联合反恐军事演习中,为了准确分析形势,军方在地面上选取相距 千米的C、D两点,以测出对方两目标A和B的距离,经测量得:∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,试求出A、B之间的距离.
跟踪训练1:
如图所示,为了计算湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测AD⊥CD,AD=5km, AB=7km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离.(假设A,B,C,D在同一平面内)
题型二 测量高度问题
例2、如图,为了测量河对岸的塔高AB,有不同的方案,其中之一是选取与塔底B在同一水平面内的两个测点C和D,测得CD=200米,在C点和D点测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.
跟踪训练2:
如下图所示,测量河岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C测得塔顶A的仰角为60°,则塔高AB=________.
题型三 测量角度问题
例3、某海上养殖基地A,接到气象部门预报,位于基地南偏东60°相距 海里的海面上有一台风中心,影响半径为20海里,正以每小时 海里的速度沿某一方向匀速直线前进,预计台风中心将从基地东北方向刮过且 小时后开始影响基地持续2小时,求台风移动的方向.
南
D
C
B
A
60°
解:如图所示,设预报时台风中心为B,开始影响基地时台风中心为C,基地刚好不受影响时台风中心为D,
则B、C、D在一条直线上,且AD=20、AC=20.
跟踪训练3:在海岸A处发现北偏东45°距离A处 海里的B处有一艘走私船,在A处北偏西75°的方向,距离A处2海里的C处的缉私船奉命以 海里/小时的速度追截走私船.此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船什么方向能最快追上走私船?
解:如图若要最快追上走私船,则两船到D点时所用时间相等.
假设在D处相遇,设缉私船用t h在D处追上走私船,如图.
则有CD= ,BD=10t
题型三 测量角度问题
例3、在某点B处测得建筑物AE的顶端A的仰角为q,沿BE方向前进30m,至点C处测得顶端A的仰角为2q,再继续前进 至D点,测得顶端A的仰角为4q,求q的大小和建筑物AE的高.
A
B
C
D
E
课后练习
1、在相距2km的A、B两点处测量目标点C,若∠CAB=750, ∠CBA=600,则A、C两点之间的距离是______km.
2、在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( )
A
3、一艘船以32n mile / h的速度向正北航行。在A处看灯塔S在船的北偏东45o的方向,30min后航行到B处,在B处看灯塔在船的北偏东75o的方向,已知距离此灯塔20n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
450
750
