2.1.1正弦定理-2019-2020学年北师大版高中数学必修五课件(共48张PPT)
文档属性
| 名称 | 2.1.1正弦定理-2019-2020学年北师大版高中数学必修五课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 22:17:15 | ||
图片预览











文档简介
数 学
必修⑤ · 北师大版
新课标导学
第二章
解三角形
在本章“解三角形”的引言中,我们遇到这么一个问题,“遥不可及的月亮离地球究竟有多远呢?”在古代,天文学家没有先进的仪器就已经估算出了两者的距离,那么,他们是用什么神奇的方法探索到这个奥秘的呢?我们知道,对于未知的距离、高度等,存在着许多可供选择的测量方案,比如可以应用全等三角形、相似三角形的方法,或借助解直角三角形的方法.阿基米德说过:“给我一个支点,我可以撬起地球.”但实际情况是根本找不到这样的支点.全等三角形法有时就像这样,你根本没有足够的空间去构造出全等三角形,所以每种方法都有它的局限性.其实上面介绍的问题是用以前的方法所不能解决的,从本章我们开始学习正弦定理、余弦定理以及它们在科学实践中的应用,看看它们能解决这个问题吗?
本章的主要内容包括正弦定理、余弦定理以及正弦定理和余弦定理的推导,解三角形及正弦定理、余弦定理在解斜三角形中的应用.
知识线索:本章是在学习了三角函数、平面向量等知识的基础上,进一步学习如何解三角形的.正、余弦定理是我们学习有关三角形知识的继续和发展,它们进一步揭示了三角形边与角之间的关系,在生产、生活中有着广泛的应用,是我们求解三角形的重要工具.本章内容与三角形的结论相联系,同时与三角函数、向量相联系,也体现了三角函数、向量及其运算的应用.高考中常与三角函数和向量知识联系起来考查,是高考的一个热点内容.
§1 正弦定理与余弦定理
第1课时 正弦定理
1
自主预习学案
2
互动探究学案
3
课时作业学案
自主预习学案
在雷达兵的训练中,有一个项目叫“捉鬼(战士语)”,即准确地发现敌台的位置.在该项目的训练中,追寻方的安排是以两个小组作为一个基本单位去执行任务,用战士的话说就是两条线(即用两台探测器分别探出敌台的方向)一交叉就把敌人给“叉”出来了,想藏?想跑?门都没有.
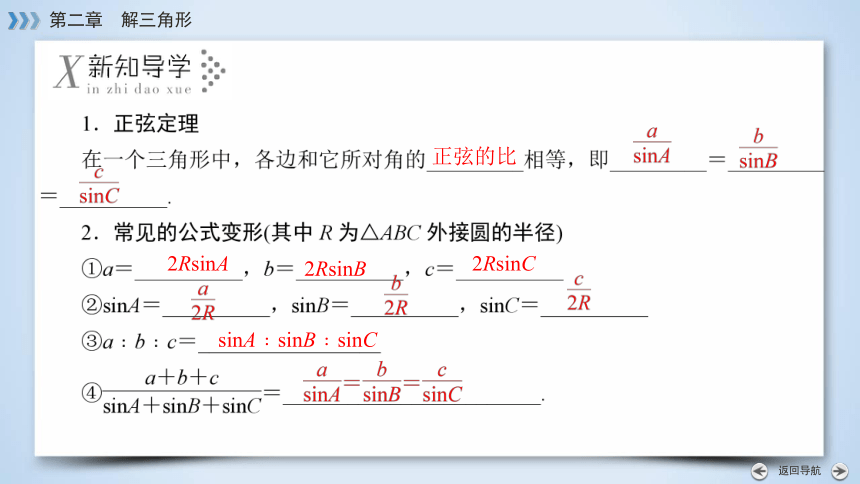
正弦的比
2RsinA
2RsinB
2RsinC
sinA﹕sinB﹕sinC
A
A
C
1
2
互动探究学案
命题方向1 ?已知两角及一边解三角形
在△ABC中,已知∠A=45°,∠B=30°,c=10,求b.
[分析] 先利用三角形内角和定理求角C,再利用正弦定理求边b.
例题 1
『规律总结』 本题属于已知两角与一边求解三角形的类型,此类问题的基本解法是:
(1)若所给边是已知角的对边时,可由正弦定理求另一边,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求第三个角,再由正弦定理求另外两边.
〔跟踪练习1〕
在△ABC中,已知B=45°,C=60°,c=1,求最短边的边长.
命题方向2 ?已知两边及一边对角解三角形
例题 2
『规律总结』 利用正弦定理解三角形,若已知三角形的两边和其中一边的对角,求另一边的对角,进而求出其他的边和角时,可能出现一解、两解或无解的情况,应结合图形并根据“三角形中大边对大角”来判断解的情况,作出正确取舍.
利用正弦定理解三角形的类型
(1)已知两角与一边,用正弦定理,有解时,只有一解.
(2)已知两边及其中一边的对角,用正弦定理,可能有两解、一解或无解,在△ABC中,已知a,b和∠A时,解的情况如下:
[分析] 已知两边及其一边对角的值,求其他边和角可先利用正弦定理求另一边对角的正弦值,或利用三角形中大边对大角考虑解的情况,可由正弦定理求其他边和角.
命题方向3 ?求三角形的面积
例题 3
命题方向4 ?利用正弦定理判断三角形形状
在△ABC中,已知a2tanB=b2tanA,试判断△ABC的形状.
例题 4
命题方向5 ?正弦定理的综合应用
例题 5
『规律总结』 利用正弦定理可以解决两类解三角形问题:一类是已知两角和任一边,求其他两边和一角;另一类是已知两边和其中一边的对角,求另一边的对角,进而求出其他的边和角.值得注意的是已知三角形的任意两 边与其中一边的对角,运用正弦定理解三角形时,解可能不唯一,可结合图形,利用大边对大角的性质去判断解的个数.要注意正弦定理的变式在解题中的应用,在解题时体会分类整合、数形结合、等价转化等数学思想方法的应用.
例题 6
课 时 作 业 学 案
必修⑤ · 北师大版
新课标导学
第二章
解三角形
在本章“解三角形”的引言中,我们遇到这么一个问题,“遥不可及的月亮离地球究竟有多远呢?”在古代,天文学家没有先进的仪器就已经估算出了两者的距离,那么,他们是用什么神奇的方法探索到这个奥秘的呢?我们知道,对于未知的距离、高度等,存在着许多可供选择的测量方案,比如可以应用全等三角形、相似三角形的方法,或借助解直角三角形的方法.阿基米德说过:“给我一个支点,我可以撬起地球.”但实际情况是根本找不到这样的支点.全等三角形法有时就像这样,你根本没有足够的空间去构造出全等三角形,所以每种方法都有它的局限性.其实上面介绍的问题是用以前的方法所不能解决的,从本章我们开始学习正弦定理、余弦定理以及它们在科学实践中的应用,看看它们能解决这个问题吗?
本章的主要内容包括正弦定理、余弦定理以及正弦定理和余弦定理的推导,解三角形及正弦定理、余弦定理在解斜三角形中的应用.
知识线索:本章是在学习了三角函数、平面向量等知识的基础上,进一步学习如何解三角形的.正、余弦定理是我们学习有关三角形知识的继续和发展,它们进一步揭示了三角形边与角之间的关系,在生产、生活中有着广泛的应用,是我们求解三角形的重要工具.本章内容与三角形的结论相联系,同时与三角函数、向量相联系,也体现了三角函数、向量及其运算的应用.高考中常与三角函数和向量知识联系起来考查,是高考的一个热点内容.
§1 正弦定理与余弦定理
第1课时 正弦定理
1
自主预习学案
2
互动探究学案
3
课时作业学案
自主预习学案
在雷达兵的训练中,有一个项目叫“捉鬼(战士语)”,即准确地发现敌台的位置.在该项目的训练中,追寻方的安排是以两个小组作为一个基本单位去执行任务,用战士的话说就是两条线(即用两台探测器分别探出敌台的方向)一交叉就把敌人给“叉”出来了,想藏?想跑?门都没有.
正弦的比
2RsinA
2RsinB
2RsinC
sinA﹕sinB﹕sinC
A
A
C
1
2
互动探究学案
命题方向1 ?已知两角及一边解三角形
在△ABC中,已知∠A=45°,∠B=30°,c=10,求b.
[分析] 先利用三角形内角和定理求角C,再利用正弦定理求边b.
例题 1
『规律总结』 本题属于已知两角与一边求解三角形的类型,此类问题的基本解法是:
(1)若所给边是已知角的对边时,可由正弦定理求另一边,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求第三个角,再由正弦定理求另外两边.
〔跟踪练习1〕
在△ABC中,已知B=45°,C=60°,c=1,求最短边的边长.
命题方向2 ?已知两边及一边对角解三角形
例题 2
『规律总结』 利用正弦定理解三角形,若已知三角形的两边和其中一边的对角,求另一边的对角,进而求出其他的边和角时,可能出现一解、两解或无解的情况,应结合图形并根据“三角形中大边对大角”来判断解的情况,作出正确取舍.
利用正弦定理解三角形的类型
(1)已知两角与一边,用正弦定理,有解时,只有一解.
(2)已知两边及其中一边的对角,用正弦定理,可能有两解、一解或无解,在△ABC中,已知a,b和∠A时,解的情况如下:
[分析] 已知两边及其一边对角的值,求其他边和角可先利用正弦定理求另一边对角的正弦值,或利用三角形中大边对大角考虑解的情况,可由正弦定理求其他边和角.
命题方向3 ?求三角形的面积
例题 3
命题方向4 ?利用正弦定理判断三角形形状
在△ABC中,已知a2tanB=b2tanA,试判断△ABC的形状.
例题 4
命题方向5 ?正弦定理的综合应用
例题 5
『规律总结』 利用正弦定理可以解决两类解三角形问题:一类是已知两角和任一边,求其他两边和一角;另一类是已知两边和其中一边的对角,求另一边的对角,进而求出其他的边和角.值得注意的是已知三角形的任意两 边与其中一边的对角,运用正弦定理解三角形时,解可能不唯一,可结合图形,利用大边对大角的性质去判断解的个数.要注意正弦定理的变式在解题中的应用,在解题时体会分类整合、数形结合、等价转化等数学思想方法的应用.
例题 6
课 时 作 业 学 案
