2.1数列的概念及简单表示法-人教A版高中数学必修五课件(34张PPT)
文档属性
| 名称 | 2.1数列的概念及简单表示法-人教A版高中数学必修五课件(34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览











文档简介
2.1 数列的概念及简单表示法
你想得到
什么样的
赏赐?
陛下,赏小
人一些麦粒就可以。
OK
请在第一个格
子放1颗麦粒
请在第二个格
子放2颗麦粒
请在第三个格
子放4颗麦粒
请在第四个格
子放8颗麦粒
依次类推……
20 21 22 23 24 25 …… ?
4
5
6
7
8
1
5
6
7
8
1
2
3
3
4
2
你认为国王有能力满足上述要求吗?
=18446744073709551615
1 2 4 8 16 32 …… ?
263
麦粒总数
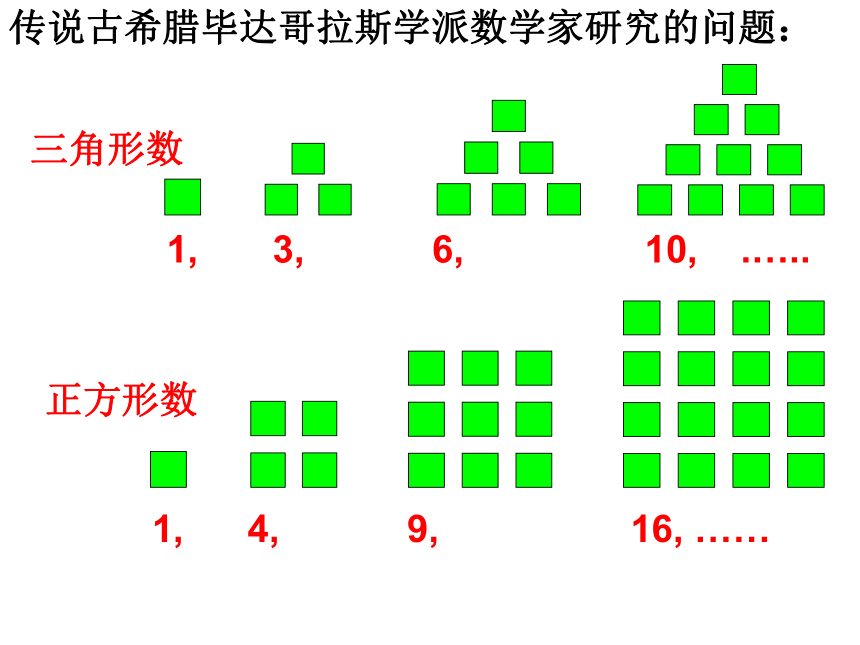
三角形数
1, 3, 6, 10, .…..
正方形数
1, 4, 9, 16, ……
传说古希腊毕达哥拉斯学派数学家研究的问题:
棋盘中各格子里的麦粒数按先后次序排成一列数:
1996~2002年某市普通高中生人数(单位:万人)排成一列数
-1的1次幂,2次幂,3次幂,……排列成一列数:
无穷多个1排列成的一列数:
三角形数:1,3,6,10,···
正方形数:1,4,9,16,···
20,21,22,23,24,25,……,263
共同特点:
1. 都是一列数;
2. 都有一定的顺序
1、定义:按一定顺序排列着的一列数称为数列
2、数列中的每一个数叫做这个数列的项。
各项依次叫做这个数列的第1项,第2项,······,第n项, ······
3、数列的一般形式可以写成:
a1,a2,a3,……,an,……
其中右下标n表示项的位置序号,上面的数列又可简记为{an}
问:an与{an}一样吗?
注意:an表示第n项,{an}表示一个数列.
一、数列的概念
4、数列的分类
(1)按项数多少分类:
(2)按增减性分类:
有穷数列,无穷数列
从第2项起,每一项都大于它的前一项的数列,即
从第2项起,每一项都小于它的前一项的数列,即
各项相等的数列.
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列.
递增数列:
递减数列:
常数列:
摆动数列:
有穷数列
无穷数列
有穷数列
无穷数列
无穷数列
递增数列
递增数列
摆动数列
常数列
20,21,22,23,24,25,……,263
1,3,6,10,···
1,4,9,16,···
递增数列
无穷数列
递增数列
如数列 2, 4, 6, …, 2n, …
数列的项数n与项an之间的关系如果可以用一个公式表示,那么这个公式叫做这个数列的通项公式。
二、数列通项公式
随堂练习
1、 根据下面数列的通项公式,写出前5项.
-1,2,-3,4,-5
1,-2,3,-4,5
经验:(-1)n可以实现符号的交替变换
2、写出数列的一个通项公式,使它的前4项分别是下列各数:
(1)1,3,5,7;
解:此数列的前四项1,3,5,7都是序号的2倍减去1,所以通项公式是:
(2)
解:此数列的前四项的分母都是序号加1,分子都是分母的平方减去1,所以通项公式是:
(3)
解:此数列的前4项的绝对值都等于序号与序号加上1的积的倒数,且奇数项为负,偶数项为正,所以通项公式是:
(4)
解:此数列的前四项的分子都是序号的2倍,分母都是序号的2倍的平方减去1,所以通项公式是:
3、已知无穷数列7,4,3, …, ,…
(1)求这个数列的第10项;
(2) 是这个数列的第几项?
小结:通项公式的作用:
①求数列中的任一项;
②判断某个数是否数列中的项
练习
B
不是
2、观察下面数列的特点,用适当的数填空,并写出每个数列的一个通项公式:
4、以下四个数中,是数列{n(n+1)}中的一项的是 ( )
A. 380 B. 39 C. 32 D. 18
A. 第9项 B. 第10项 C. 第11项 D. 第12项
6、 数列1, -2, 3, -4, 5的一个通项公式为_______
A
C
(-1)n+1·n
D
对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.
项数n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量)
(函数值)
数列是一种特殊的函数
可以认为:
(1)数列与函数
三、通项公式的两点说明
与函数一样,数列也可以用图象、列表等方法来表示。
数列的图象是一系列孤立的点。
例如
数例: 2,4,6,8,10
n
an
0
1
2
3
4
5
2
4
6
8
10
数列的几何意义:有穷数列表示有限个孤立的点。
无穷数列表示无限个孤立的点。
1
0
-1
1
2
3
4
5
6
n
an
数列:-1, 1, -1, 1, -1…
(2)通项公式的存在性和个数问题
数列{an}的第n项an与项数n之间的关系
的数学表达式。
(1)不是每一个数列都能写出其通项公式;
(2)数列的通项公式不唯一 .如: ?1, 1, ?1, 1, …
注:
递推公式也是数列的一种表示方法。
四、数列的递推公式:
递推公式是数列所特有的表示法,
它包含两个部分,二者缺一不可.
(1)递推关系(任一项与前一项或前几项的关系式),
(2)初始条件(已知的第一项或前几项).
写出这个数列的前5项.
(1)1,6,11,16,21,…
(2)1,3,6,10,15,…
(3)3,5,8,13,21,…
例2、以下各数为数列{an}的前5项an,写出该数列的递推公式:
五、常见递推公式与通项公式的转化
例3:求以下数列的通项公式
5,8,11,14,17,…
叠加法
练习:
例4 已知a1 = 2,an+1 = 2an,求 an.
累乘法
小结:
本节课学习的主要内容有:
1、数列的定义;
2、数列的通项公式和递推公式;
3、数列的实质;
1+2+22+23+24+……+263=264-1 =18446744073709551615。 这些麦子究竟有多少?打个比方,如果造一个仓库来放这些麦子,仓库高4公尺,宽10公尺,那么仓库的长度就等于地球到太阳的距离的两倍。而要生产这么多的麦子,全世界要两千年。
你想得到
什么样的
赏赐?
陛下,赏小
人一些麦粒就可以。
OK
请在第一个格
子放1颗麦粒
请在第二个格
子放2颗麦粒
请在第三个格
子放4颗麦粒
请在第四个格
子放8颗麦粒
依次类推……
20 21 22 23 24 25 …… ?
4
5
6
7
8
1
5
6
7
8
1
2
3
3
4
2
你认为国王有能力满足上述要求吗?
=18446744073709551615
1 2 4 8 16 32 …… ?
263
麦粒总数
三角形数
1, 3, 6, 10, .…..
正方形数
1, 4, 9, 16, ……
传说古希腊毕达哥拉斯学派数学家研究的问题:
棋盘中各格子里的麦粒数按先后次序排成一列数:
1996~2002年某市普通高中生人数(单位:万人)排成一列数
-1的1次幂,2次幂,3次幂,……排列成一列数:
无穷多个1排列成的一列数:
三角形数:1,3,6,10,···
正方形数:1,4,9,16,···
20,21,22,23,24,25,……,263
共同特点:
1. 都是一列数;
2. 都有一定的顺序
1、定义:按一定顺序排列着的一列数称为数列
2、数列中的每一个数叫做这个数列的项。
各项依次叫做这个数列的第1项,第2项,······,第n项, ······
3、数列的一般形式可以写成:
a1,a2,a3,……,an,……
其中右下标n表示项的位置序号,上面的数列又可简记为{an}
问:an与{an}一样吗?
注意:an表示第n项,{an}表示一个数列.
一、数列的概念
4、数列的分类
(1)按项数多少分类:
(2)按增减性分类:
有穷数列,无穷数列
从第2项起,每一项都大于它的前一项的数列,即
从第2项起,每一项都小于它的前一项的数列,即
各项相等的数列.
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列.
递增数列:
递减数列:
常数列:
摆动数列:
有穷数列
无穷数列
有穷数列
无穷数列
无穷数列
递增数列
递增数列
摆动数列
常数列
20,21,22,23,24,25,……,263
1,3,6,10,···
1,4,9,16,···
递增数列
无穷数列
递增数列
如数列 2, 4, 6, …, 2n, …
数列的项数n与项an之间的关系如果可以用一个公式表示,那么这个公式叫做这个数列的通项公式。
二、数列通项公式
随堂练习
1、 根据下面数列的通项公式,写出前5项.
-1,2,-3,4,-5
1,-2,3,-4,5
经验:(-1)n可以实现符号的交替变换
2、写出数列的一个通项公式,使它的前4项分别是下列各数:
(1)1,3,5,7;
解:此数列的前四项1,3,5,7都是序号的2倍减去1,所以通项公式是:
(2)
解:此数列的前四项的分母都是序号加1,分子都是分母的平方减去1,所以通项公式是:
(3)
解:此数列的前4项的绝对值都等于序号与序号加上1的积的倒数,且奇数项为负,偶数项为正,所以通项公式是:
(4)
解:此数列的前四项的分子都是序号的2倍,分母都是序号的2倍的平方减去1,所以通项公式是:
3、已知无穷数列7,4,3, …, ,…
(1)求这个数列的第10项;
(2) 是这个数列的第几项?
小结:通项公式的作用:
①求数列中的任一项;
②判断某个数是否数列中的项
练习
B
不是
2、观察下面数列的特点,用适当的数填空,并写出每个数列的一个通项公式:
4、以下四个数中,是数列{n(n+1)}中的一项的是 ( )
A. 380 B. 39 C. 32 D. 18
A. 第9项 B. 第10项 C. 第11项 D. 第12项
6、 数列1, -2, 3, -4, 5的一个通项公式为_______
A
C
(-1)n+1·n
D
对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.
项数n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量)
(函数值)
数列是一种特殊的函数
可以认为:
(1)数列与函数
三、通项公式的两点说明
与函数一样,数列也可以用图象、列表等方法来表示。
数列的图象是一系列孤立的点。
例如
数例: 2,4,6,8,10
n
an
0
1
2
3
4
5
2
4
6
8
10
数列的几何意义:有穷数列表示有限个孤立的点。
无穷数列表示无限个孤立的点。
1
0
-1
1
2
3
4
5
6
n
an
数列:-1, 1, -1, 1, -1…
(2)通项公式的存在性和个数问题
数列{an}的第n项an与项数n之间的关系
的数学表达式。
(1)不是每一个数列都能写出其通项公式;
(2)数列的通项公式不唯一 .如: ?1, 1, ?1, 1, …
注:
递推公式也是数列的一种表示方法。
四、数列的递推公式:
递推公式是数列所特有的表示法,
它包含两个部分,二者缺一不可.
(1)递推关系(任一项与前一项或前几项的关系式),
(2)初始条件(已知的第一项或前几项).
写出这个数列的前5项.
(1)1,6,11,16,21,…
(2)1,3,6,10,15,…
(3)3,5,8,13,21,…
例2、以下各数为数列{an}的前5项an,写出该数列的递推公式:
五、常见递推公式与通项公式的转化
例3:求以下数列的通项公式
5,8,11,14,17,…
叠加法
练习:
例4 已知a1 = 2,an+1 = 2an,求 an.
累乘法
小结:
本节课学习的主要内容有:
1、数列的定义;
2、数列的通项公式和递推公式;
3、数列的实质;
1+2+22+23+24+……+263=264-1 =18446744073709551615。 这些麦子究竟有多少?打个比方,如果造一个仓库来放这些麦子,仓库高4公尺,宽10公尺,那么仓库的长度就等于地球到太阳的距离的两倍。而要生产这么多的麦子,全世界要两千年。
