2.4等比数列-人教A版高中数学必修五课件(36张PPT)
文档属性
| 名称 | 2.4等比数列-人教A版高中数学必修五课件(36张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览










文档简介
2.4 等比数列
引例:
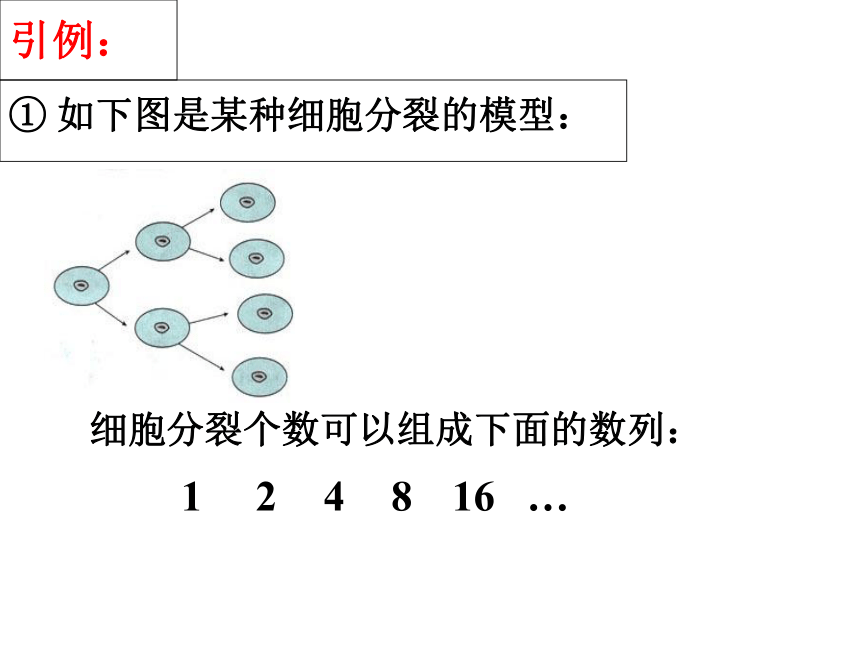
① 如下图是某种细胞分裂的模型:
细胞分裂个数可以组成下面的数列:
1
2
4
8
16
…
②我国古代一些学者提出:“一尺之棰,日取其半,万世不竭。”用现代语言叙述为:一尺长的木棒,每日取其一半,永远也取不完。这样,每日剩下的部分都是前一日的一半。如果把“一尺之棰”看成单位“1”,那么,得到的数列是:
1
…
引例:
取出这些数列,观察:有什么共同特征?
一、探究发现
1,2,4,8,16,……
共同特征:
从第二项起,每一项与它的前一项的比都等于同一常数。
(一)定义:
一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一常数,那么这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。
理解:
1)公差d可为0,公比q不可以为0。且每一项不为0;
2)公比是每一项与其前一项之比,防止前后次序颠倒。
3)证明一个数列为等比数列,其依据是
4)常数列都是等差数列,但不一定是等比数列。
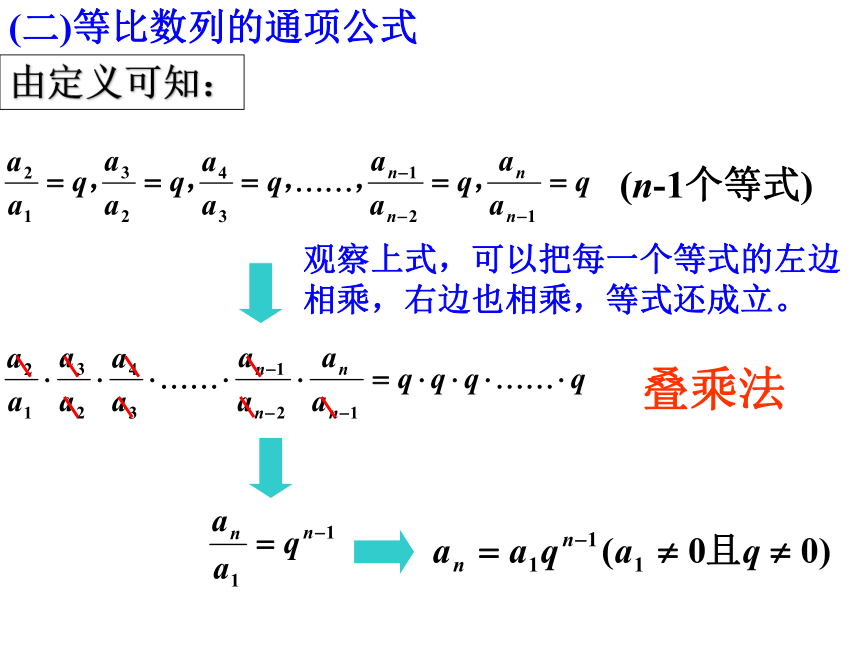
由定义可知:
观察上式,可以把每一个等式的左边相乘,右边也相乘,等式还成立。
叠乘法
(二)等比数列的通项公式
(n-1个等式)
对于等比数列中的任意两项an,am
(三)等比数列的推导公式
例1、一个等比数列的第3项与第4项分别是12与18 ,求它的通项公式与第2项.
解:设首项为a1,公比为q,则有
解得
解得
因此,an=5×2n-1
例2、在等比数列{an}中,已知a3=20,a6=160,求an.
解:设等比数列{an}的公比为q,由题意得
-729
9
小结:
1、注意在等比数列中,遇到q的偶次方要注意解的个数。
2、在等比数列的方程中常用的乘,除运算
3、在一些特定问题中, 可以整体运算。
随堂练习
1、下列叙述中正确的是( )
A、等比数列的首项不能为零,但公比可以为零。
B、等比数列的公比q>0时,是递增数列。
C、若数列{an}为常数列,则此数列为等比数列。
D、已知等比数列{an}的通项公式an=(-2)n,则它的公比为-2。
D
2、数列m,m,m,…,m,…( )
A、一定是等比数列
B、既是等差数列又是等比数列
C、一定是等差数列,不一定是等比数列
D、既不是等差数列,也不是等比数列
C
3、已知数列a,a(a-1),a(1-a)2,…是等比数列,则实数a满足
A、a≠1 B、a≠0或a≠1 C、a≠0 D、a≠1且a≠0
D
A
4
7、等差数列{an}中,a1=2,公差不为0,且a1,a3,a11恰好是某等比数列的前三项,那么该等比数列公比的值等于__________
220
4
观察如下的两个数之间,插入一个什么数后三个数就会成为一个等比数列:
(1)1, ,9 (2)-1, ,-4
(3)-12, ,-3 (4)1, ,1
±3
±2
±6
±1
若a,G,b成等比数列,那么G叫做a与b的等比中项。
(四)等比中项
±4
练习
(1)已知等比数列{an},a3=7,a7=21,则a5 = ( )
A. 35 B. 63 C. D.
(2)已知等比数列{an},a3=7,a7=21,则a3和a7 的等比中项是( )
A. 35 B. 63 C. D.
C
D
例题:
2、已知{an}是等比数列且an>0,a2a4+2a3a5+a4a6=25,求a3+a5
5
1.在等比数列{an}中,a5=4,a7=6,求a9
3. 在2和30之间插入两个正数,使前3个数依次成等比数列,后三个数依次成等差数列,求插入的这两个正数.
9
9
6、18
巩固练习
4.三个正数a,b,c成等比数列,且a+b+c=62, lga+lgb+lgc=3,则这三个正数为 .
50,10,2或2,10,50
1、若m,n,p,q∈N+,且m+n=p+q,则am·an=aq·ap.
特别的,若2m=p+q, 则am2=apaq
(五)等比数列的性质
4、等比数列所有奇数项符号相同;
所有偶数项符号相同。
(五)等比数列的性质
例题
9
±3
C
81
1、在等比数列{an}中,若a4·a8=9,则a2·a10=____,a6=____,a2·a3·a9·a10=____.
2、在正项等比数列{an}中,若a5·a6=81,则log3a1+log3a2+……+log3a10的值是( )
A、5 B、10 C、20 D、2
9
练习:
2、在等比数列{an}中, a3a4a5=3,a6a7a8=24,则a9a10a11=( )
A. 48 B. 72 C. 144 D. 192
D
A
3、在正项等比数列{an}中,lga3+lga6+lga9=6,则a1a11的值是
A.10 000 B.1 000 C.100 D.10
例3、已知等比数列{an}中,a2+a5=18,a3a4=45,求通项公式an.
练习:
1、在等比数列{an}中,a2a8=36,a1+a9=15,求通项公式an.
3、在等比数列{an}中,a2+a3+a4=28,a3+2
是a2、a4的等差中项,求an.
2、在等比数列{an}中,若a1+a2+a3=7,a1·a2·a3=8,求an.
2、已知递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2、a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log2an+1,Sn是数列{bn}的前n项和,求使Sn>42+4n成立的n的最小值.
例1、已知三个数成等比数列,且其积为512,若第一个数与第三个数各减2,则成等差数列,求这三数。
二、综合应用
练习
1、三数成等比数列,积为27,和为13,求这三个数。
2、三数成等比数列,若将第三个数减去32,则成等差数列,若再将这等差数列的第二个数减去4,则又成等比数列,求原来三个数。
例2、已知数列{an}满足a1=1,an+1=2an+1.
1)求证数列{an+1}是等比数列;
2)求an的表达式
解:1)∵an+1=2an+1.∴ an+1+1=2(an+1)
所以数列{an+1}是等比数列;
2) 由1)知数列{an+1}的首项是a1+1=2,公比是q=2,所以an+1=2×2n-1=2n
∴an=2n-1
例2、已知数列{an}满足a1=1,an+1=2an+1.求an的表达式
若数列有形如an=pan-1+q(p、q为常数,pq≠0,p≠1) 的线性递推关系,则可用待定系数法设an+m=p(an-1+m)求得an
解二:设an+m=2(an-1+m),∴ an=2an-1+m,
又an=2an-1+1,∴m=1,
所以an+1=2(an-1+1)
所以{an+1}是以a1+1=2为首项,2为公比的等比数列
所以an+1=2·2n-1=2n,所以an=2n-1
练习:
1、已知数列{an}满足a1=2,an+1=3an+2.求an的表达式
例3、在等比数列{an}中,S3= 42 ,a2 + a3 + a4 = 84,求an .
C
216
小结
1、理解等比数列的概念
2、判定一个数列是等比数列,不能只验证数列的前几项,需根据定义证明an+1:an是非零常数。也可证明an2=an-1an+1 (n≥2)
3、等比数列的通项公式联系着4个基本量a1,q,n,an。
“知三求第四”是一类最基本的运算问题,注意运用函数与方程思想,整体思想,分类讨论的思想等分析问题和解决问题。
引例:
① 如下图是某种细胞分裂的模型:
细胞分裂个数可以组成下面的数列:
1
2
4
8
16
…
②我国古代一些学者提出:“一尺之棰,日取其半,万世不竭。”用现代语言叙述为:一尺长的木棒,每日取其一半,永远也取不完。这样,每日剩下的部分都是前一日的一半。如果把“一尺之棰”看成单位“1”,那么,得到的数列是:
1
…
引例:
取出这些数列,观察:有什么共同特征?
一、探究发现
1,2,4,8,16,……
共同特征:
从第二项起,每一项与它的前一项的比都等于同一常数。
(一)定义:
一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一常数,那么这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。
理解:
1)公差d可为0,公比q不可以为0。且每一项不为0;
2)公比是每一项与其前一项之比,防止前后次序颠倒。
3)证明一个数列为等比数列,其依据是
4)常数列都是等差数列,但不一定是等比数列。
由定义可知:
观察上式,可以把每一个等式的左边相乘,右边也相乘,等式还成立。
叠乘法
(二)等比数列的通项公式
(n-1个等式)
对于等比数列中的任意两项an,am
(三)等比数列的推导公式
例1、一个等比数列的第3项与第4项分别是12与18 ,求它的通项公式与第2项.
解:设首项为a1,公比为q,则有
解得
解得
因此,an=5×2n-1
例2、在等比数列{an}中,已知a3=20,a6=160,求an.
解:设等比数列{an}的公比为q,由题意得
-729
9
小结:
1、注意在等比数列中,遇到q的偶次方要注意解的个数。
2、在等比数列的方程中常用的乘,除运算
3、在一些特定问题中, 可以整体运算。
随堂练习
1、下列叙述中正确的是( )
A、等比数列的首项不能为零,但公比可以为零。
B、等比数列的公比q>0时,是递增数列。
C、若数列{an}为常数列,则此数列为等比数列。
D、已知等比数列{an}的通项公式an=(-2)n,则它的公比为-2。
D
2、数列m,m,m,…,m,…( )
A、一定是等比数列
B、既是等差数列又是等比数列
C、一定是等差数列,不一定是等比数列
D、既不是等差数列,也不是等比数列
C
3、已知数列a,a(a-1),a(1-a)2,…是等比数列,则实数a满足
A、a≠1 B、a≠0或a≠1 C、a≠0 D、a≠1且a≠0
D
A
4
7、等差数列{an}中,a1=2,公差不为0,且a1,a3,a11恰好是某等比数列的前三项,那么该等比数列公比的值等于__________
220
4
观察如下的两个数之间,插入一个什么数后三个数就会成为一个等比数列:
(1)1, ,9 (2)-1, ,-4
(3)-12, ,-3 (4)1, ,1
±3
±2
±6
±1
若a,G,b成等比数列,那么G叫做a与b的等比中项。
(四)等比中项
±4
练习
(1)已知等比数列{an},a3=7,a7=21,则a5 = ( )
A. 35 B. 63 C. D.
(2)已知等比数列{an},a3=7,a7=21,则a3和a7 的等比中项是( )
A. 35 B. 63 C. D.
C
D
例题:
2、已知{an}是等比数列且an>0,a2a4+2a3a5+a4a6=25,求a3+a5
5
1.在等比数列{an}中,a5=4,a7=6,求a9
3. 在2和30之间插入两个正数,使前3个数依次成等比数列,后三个数依次成等差数列,求插入的这两个正数.
9
9
6、18
巩固练习
4.三个正数a,b,c成等比数列,且a+b+c=62, lga+lgb+lgc=3,则这三个正数为 .
50,10,2或2,10,50
1、若m,n,p,q∈N+,且m+n=p+q,则am·an=aq·ap.
特别的,若2m=p+q, 则am2=apaq
(五)等比数列的性质
4、等比数列所有奇数项符号相同;
所有偶数项符号相同。
(五)等比数列的性质
例题
9
±3
C
81
1、在等比数列{an}中,若a4·a8=9,则a2·a10=____,a6=____,a2·a3·a9·a10=____.
2、在正项等比数列{an}中,若a5·a6=81,则log3a1+log3a2+……+log3a10的值是( )
A、5 B、10 C、20 D、2
9
练习:
2、在等比数列{an}中, a3a4a5=3,a6a7a8=24,则a9a10a11=( )
A. 48 B. 72 C. 144 D. 192
D
A
3、在正项等比数列{an}中,lga3+lga6+lga9=6,则a1a11的值是
A.10 000 B.1 000 C.100 D.10
例3、已知等比数列{an}中,a2+a5=18,a3a4=45,求通项公式an.
练习:
1、在等比数列{an}中,a2a8=36,a1+a9=15,求通项公式an.
3、在等比数列{an}中,a2+a3+a4=28,a3+2
是a2、a4的等差中项,求an.
2、在等比数列{an}中,若a1+a2+a3=7,a1·a2·a3=8,求an.
2、已知递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2、a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log2an+1,Sn是数列{bn}的前n项和,求使Sn>42+4n成立的n的最小值.
例1、已知三个数成等比数列,且其积为512,若第一个数与第三个数各减2,则成等差数列,求这三数。
二、综合应用
练习
1、三数成等比数列,积为27,和为13,求这三个数。
2、三数成等比数列,若将第三个数减去32,则成等差数列,若再将这等差数列的第二个数减去4,则又成等比数列,求原来三个数。
例2、已知数列{an}满足a1=1,an+1=2an+1.
1)求证数列{an+1}是等比数列;
2)求an的表达式
解:1)∵an+1=2an+1.∴ an+1+1=2(an+1)
所以数列{an+1}是等比数列;
2) 由1)知数列{an+1}的首项是a1+1=2,公比是q=2,所以an+1=2×2n-1=2n
∴an=2n-1
例2、已知数列{an}满足a1=1,an+1=2an+1.求an的表达式
若数列有形如an=pan-1+q(p、q为常数,pq≠0,p≠1) 的线性递推关系,则可用待定系数法设an+m=p(an-1+m)求得an
解二:设an+m=2(an-1+m),∴ an=2an-1+m,
又an=2an-1+1,∴m=1,
所以an+1=2(an-1+1)
所以{an+1}是以a1+1=2为首项,2为公比的等比数列
所以an+1=2·2n-1=2n,所以an=2n-1
练习:
1、已知数列{an}满足a1=2,an+1=3an+2.求an的表达式
例3、在等比数列{an}中,S3= 42 ,a2 + a3 + a4 = 84,求an .
C
216
小结
1、理解等比数列的概念
2、判定一个数列是等比数列,不能只验证数列的前几项,需根据定义证明an+1:an是非零常数。也可证明an2=an-1an+1 (n≥2)
3、等比数列的通项公式联系着4个基本量a1,q,n,an。
“知三求第四”是一类最基本的运算问题,注意运用函数与方程思想,整体思想,分类讨论的思想等分析问题和解决问题。
