3.2.1一元二次不等式及其解法-人教A版高中数学必修五课件(27张PPT)
文档属性
| 名称 | 3.2.1一元二次不等式及其解法-人教A版高中数学必修五课件(27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 23:03:18 | ||
图片预览





文档简介
3.2.1一元二次不等式及其解法
观察下面含未知数x的不等式:
15x2+30x-1>0 和 x2+6x-1≤0.
它们有什么共同特点:
(1)含有一个未知数x;
(2)未知数的最高次数为2.
1.一元二次不等式
定义:一般地,把只含有一个未知数,
且未知数的最高次数为2的不等式,
叫做一元二次不等式。
y
O
x
5
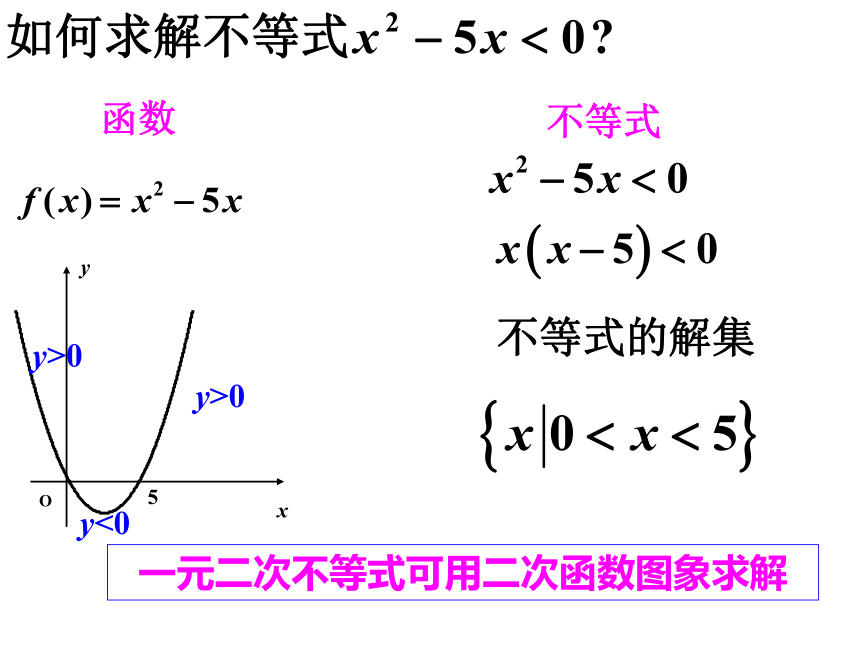
函数
方程
不等式
方程的解
不等式的解集
y>0
y>0
y<0
二次不等式与二次函数、二次方程的关系
y
O
x
5
函数
不等式的解集
y>0
y>0
y<0
一元二次不等式可用二次函数图象求解
不等式
方程的解即函数图象与x轴交点的横坐标
不等式的解集即函数图象在x轴下方或上方图象所对应x的范围。
利用二次函数图象能解一元二次不等式!
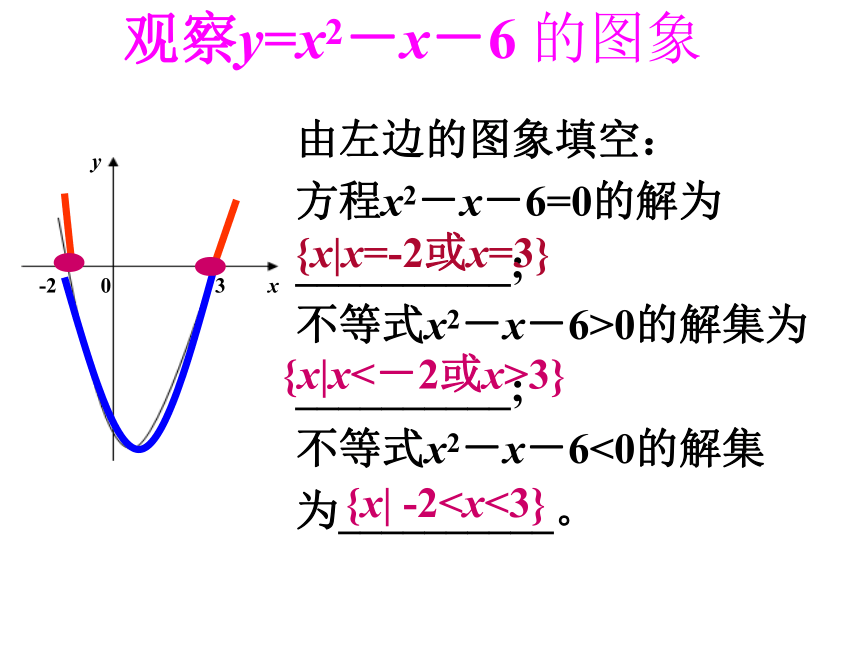
由左边的图象填空:
方程x2-x-6=0的解为
__________;
不等式x2-x-6>0的解集为
__________;
不等式x2-x-6<0的解集
为__________。
-2
0
3
x
y
{x|x=-2或x=3}
{x|x<-2或x>3}
{x| -2观察y=x2-x-6 的图象
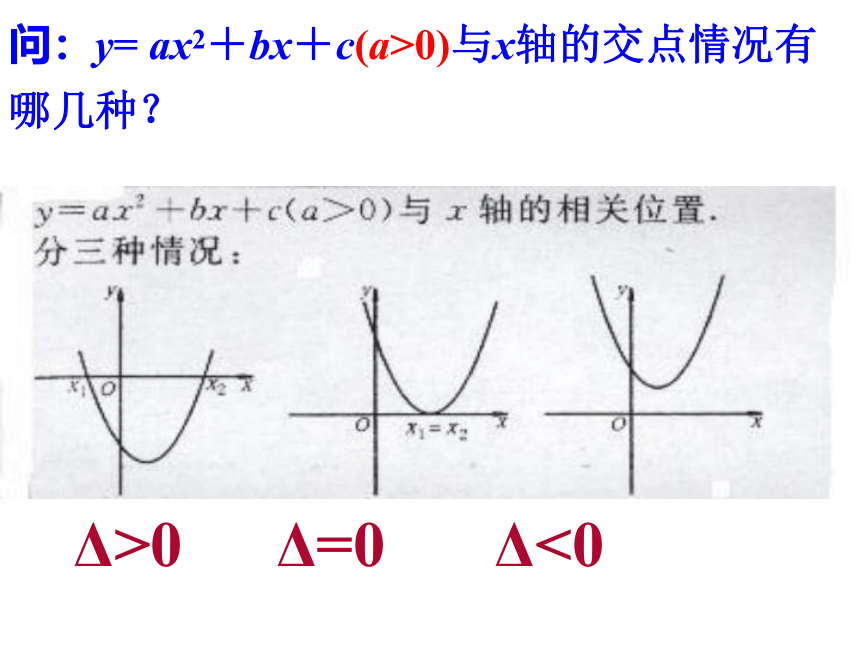
问:y= ax2+bx+c(a>0)与x轴的交点情况有哪几种?
Δ>0 Δ=0 Δ<0
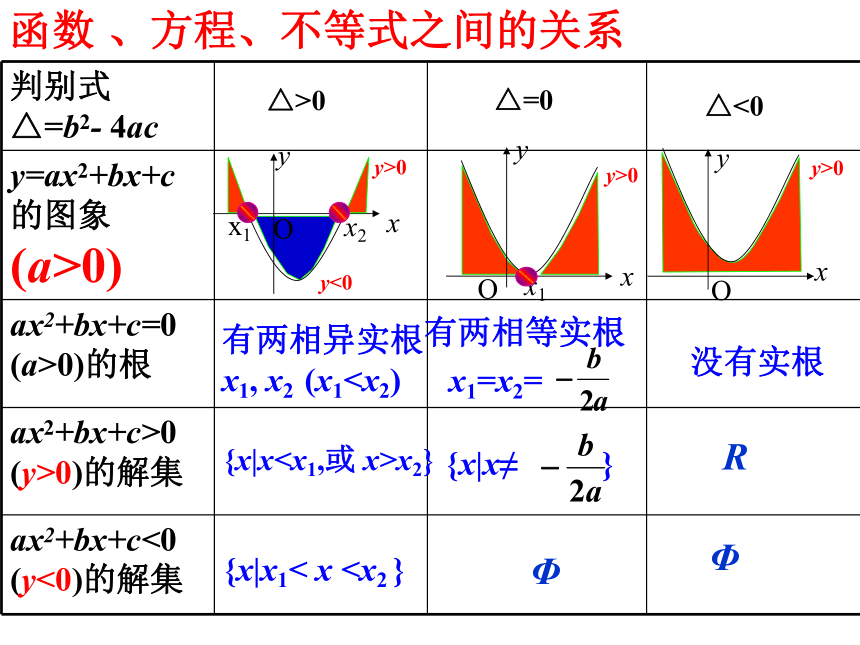
判别式
△=b2- 4ac
y=ax2+bx+c
的图象
(a>0)
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(y>0)的解集
ax2+bx+c<0
(y<0)的解集
△>0
有两相异实根
x1, x2 (x1{x|xx2}
{x|x1< x△=0
△<0
有两相等实根
x1=x2=
{x|x≠ }
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
函数 、方程、不等式之间的关系
y>0
y>0
y>0
y<0
△>0
△=0
△<0
判别式
△=b2-4ac
(a>0)的解集
ax2+bx+c<0
{x | x1?
?
一元二次方程
ax2+bx+c=0
(a>0) 的根
有两相异实根
x1, x2 (x1没有实根
有两相等实根
x1=x2= -
2a
b
(a>0)的解集
R
ax2+bx+c>0
{x | xx2}
{x | x≠- }
2a
b
二次函数与方程、不等式的关系
(a>0)的图象
二次函数
y=ax2+bx+c
o
x
y
x1
x2
x1=x2
x
y
o
o
x
y
求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图:
△≥0
x< x1或x> x2
例1、解不等式 2x2-3x-2>0.
解:因为△ =(-3)2-4×2×(-2)>0,
方程2x2-3x-2 =0的解是
所以,原不等式的解集是
先求方程的根
然后想像图象形状
注:开口向上,大于0
解集是大于大根,小于小根
解:原不等式可化为:
所以,不等式的解集是
说明:数形结合要牢记心中,但书写过程可简化。
另解:
例1、解不等式 2x2-3x-2>0
例2:解不等式 - 2x2 + 3x +5 >0
解:整理,得 2x2 - 3x - 5< 0
因为△= 9+40 = 49 > 0
另解?
例4 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值y(元)之间有如下的关系: y =-2x2 + 220x.
若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车?
解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 -110x+3000<0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根
x1=50, x2=60.
由函数y=x2-110x+3000的图象,
得不等式的解为50 因为x只能取整数,所以当这条摩托
车整车装配流水线在一周内生产的摩托
车数量在51辆到59辆之间时,这家工厂
能够获得6000元以上的收益.
归纳:解一元二次不等式的一般步骤
(1)对不等式变形,使一端为零且二次项系数大于零;
(2)计算相应的判别式;
(3)当△>0时,求出相应的一元二次方程的两个根;
(5)根据函数图像写出一元二次不等式的解集。
(4)画出相应二次函数的草图;
记忆口诀: (前提a>0).
大于取两边,小于取中间
练习1、解不等式 4x2-4x+1 > 0
解一:因为△ =0,方程4x2-4x+1 =0的解是
所以,原不等式的解集是
变式:4x2-4x+1 <0
无解
解二:原不等式可化为
所以,原不等式的解集是
变式:4x2-4x+1 <0
无解
练习1、解不等式 4x2-4x+1 > 0
练习2、解不等式 -3x2+6x > 2
解: ∵-3x2+6x > 2
∴3x2-6x+2 < 0
∵方程的解3x2-6x+2 =0的解是
所以,原不等式的解集是
练习3、解不等式 -x2 +2x-3 > 0
解: ∵-x2 +2x-3 > 0
∴ x2 -2x+3 < 0
变式: x2 -2x+3 >0
∵△= -8<0
∴ 方程x2 -2x+3 = 0无实数根
∴ 原不等式的解集为空集
例3 、已知一元二次不等式ax2 +bx+6>0
的解集为{x |-2 解:由条件可知 :
方程a x2 +bx+6=0的根-2,3
又解在两根之间;
∴a<0
思考题:
R
-12
-2
-2≤a≤6
练习:求函数 的定义域。
变式:若 的定义域为R,求b范围。
课外作业:
变式:若对于x∈R,不等式mx2+2mx+3>0恒成立,求实数m的取值范围。
分析:此题需要对m的取值进行讨论.
课本80页第3、4题
作业与思考:
拓展:若 的值域为R,
求b范围。
课后思考:
解不等式
x2 + 5ax + 6a2 > 0
观察下面含未知数x的不等式:
15x2+30x-1>0 和 x2+6x-1≤0.
它们有什么共同特点:
(1)含有一个未知数x;
(2)未知数的最高次数为2.
1.一元二次不等式
定义:一般地,把只含有一个未知数,
且未知数的最高次数为2的不等式,
叫做一元二次不等式。
y
O
x
5
函数
方程
不等式
方程的解
不等式的解集
y>0
y>0
y<0
二次不等式与二次函数、二次方程的关系
y
O
x
5
函数
不等式的解集
y>0
y>0
y<0
一元二次不等式可用二次函数图象求解
不等式
方程的解即函数图象与x轴交点的横坐标
不等式的解集即函数图象在x轴下方或上方图象所对应x的范围。
利用二次函数图象能解一元二次不等式!
由左边的图象填空:
方程x2-x-6=0的解为
__________;
不等式x2-x-6>0的解集为
__________;
不等式x2-x-6<0的解集
为__________。
-2
0
3
x
y
{x|x=-2或x=3}
{x|x<-2或x>3}
{x| -2
问:y= ax2+bx+c(a>0)与x轴的交点情况有哪几种?
Δ>0 Δ=0 Δ<0
判别式
△=b2- 4ac
y=ax2+bx+c
的图象
(a>0)
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(y>0)的解集
ax2+bx+c<0
(y<0)的解集
△>0
有两相异实根
x1, x2 (x1
{x|x1< x
△<0
有两相等实根
x1=x2=
{x|x≠ }
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
函数 、方程、不等式之间的关系
y>0
y>0
y>0
y<0
△>0
△=0
△<0
判别式
△=b2-4ac
(a>0)的解集
ax2+bx+c<0
{x | x1
?
一元二次方程
ax2+bx+c=0
(a>0) 的根
有两相异实根
x1, x2 (x1
有两相等实根
x1=x2= -
2a
b
(a>0)的解集
R
ax2+bx+c>0
{x | x
{x | x≠- }
2a
b
二次函数与方程、不等式的关系
(a>0)的图象
二次函数
y=ax2+bx+c
o
x
y
x1
x2
x1=x2
x
y
o
o
x
y
求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图:
△≥0
x< x1或x> x2
例1、解不等式 2x2-3x-2>0.
解:因为△ =(-3)2-4×2×(-2)>0,
方程2x2-3x-2 =0的解是
所以,原不等式的解集是
先求方程的根
然后想像图象形状
注:开口向上,大于0
解集是大于大根,小于小根
解:原不等式可化为:
所以,不等式的解集是
说明:数形结合要牢记心中,但书写过程可简化。
另解:
例1、解不等式 2x2-3x-2>0
例2:解不等式 - 2x2 + 3x +5 >0
解:整理,得 2x2 - 3x - 5< 0
因为△= 9+40 = 49 > 0
另解?
例4 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值y(元)之间有如下的关系: y =-2x2 + 220x.
若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车?
解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 -110x+3000<0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根
x1=50, x2=60.
由函数y=x2-110x+3000的图象,
得不等式的解为50
车整车装配流水线在一周内生产的摩托
车数量在51辆到59辆之间时,这家工厂
能够获得6000元以上的收益.
归纳:解一元二次不等式的一般步骤
(1)对不等式变形,使一端为零且二次项系数大于零;
(2)计算相应的判别式;
(3)当△>0时,求出相应的一元二次方程的两个根;
(5)根据函数图像写出一元二次不等式的解集。
(4)画出相应二次函数的草图;
记忆口诀: (前提a>0).
大于取两边,小于取中间
练习1、解不等式 4x2-4x+1 > 0
解一:因为△ =0,方程4x2-4x+1 =0的解是
所以,原不等式的解集是
变式:4x2-4x+1 <0
无解
解二:原不等式可化为
所以,原不等式的解集是
变式:4x2-4x+1 <0
无解
练习1、解不等式 4x2-4x+1 > 0
练习2、解不等式 -3x2+6x > 2
解: ∵-3x2+6x > 2
∴3x2-6x+2 < 0
∵方程的解3x2-6x+2 =0的解是
所以,原不等式的解集是
练习3、解不等式 -x2 +2x-3 > 0
解: ∵-x2 +2x-3 > 0
∴ x2 -2x+3 < 0
变式: x2 -2x+3 >0
∵△= -8<0
∴ 方程x2 -2x+3 = 0无实数根
∴ 原不等式的解集为空集
例3 、已知一元二次不等式ax2 +bx+6>0
的解集为{x |-2
方程a x2 +bx+6=0的根-2,3
又解在两根之间;
∴a<0
思考题:
R
-12
-2
-2≤a≤6
练习:求函数 的定义域。
变式:若 的定义域为R,求b范围。
课外作业:
变式:若对于x∈R,不等式mx2+2mx+3>0恒成立,求实数m的取值范围。
分析:此题需要对m的取值进行讨论.
课本80页第3、4题
作业与思考:
拓展:若 的值域为R,
求b范围。
课后思考:
解不等式
x2 + 5ax + 6a2 > 0
