3.2.2分式不等式-人教A版高中数学必修五课件(19张PPT)
文档属性
| 名称 | 3.2.2分式不等式-人教A版高中数学必修五课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 612.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 23:05:14 | ||
图片预览




文档简介
分式不等式
数轴标根法
复习:解一元二次不等式的一般步骤
(1)对不等式变形,使一端为零且二次项系数大于零;
(2)计算相应的判别式;
(3)当△>0时,求出相应的一元二次方程的两个根;
(5)根据函数图像写出一元二次不等式的解集。
(4)画出相应二次函数的草图;
记忆口诀: (前提a>0).
大于取两边,小于取中间
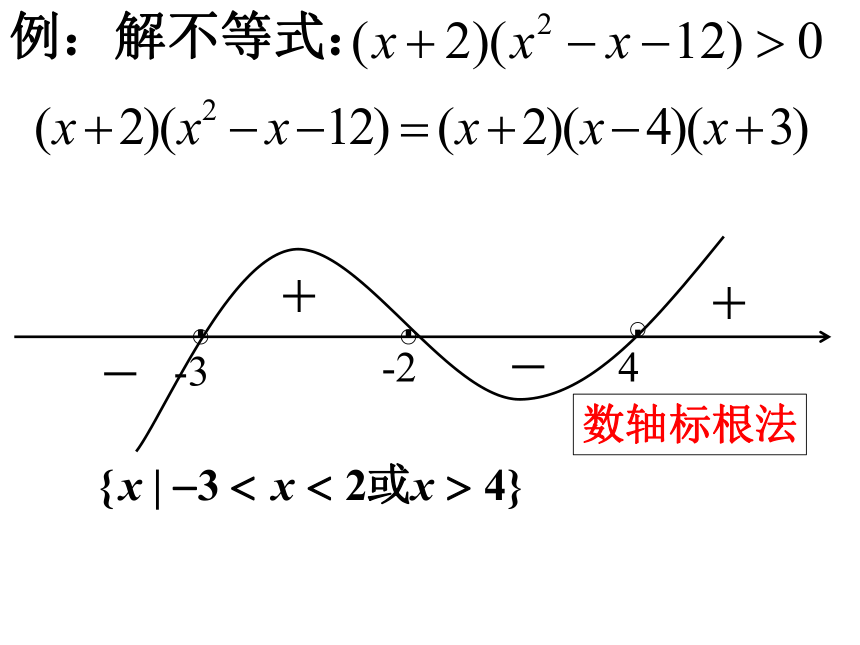
例:解不等式:
分析:
x的取
值范围
-3
4
-2
例:解不等式:
数轴标根法
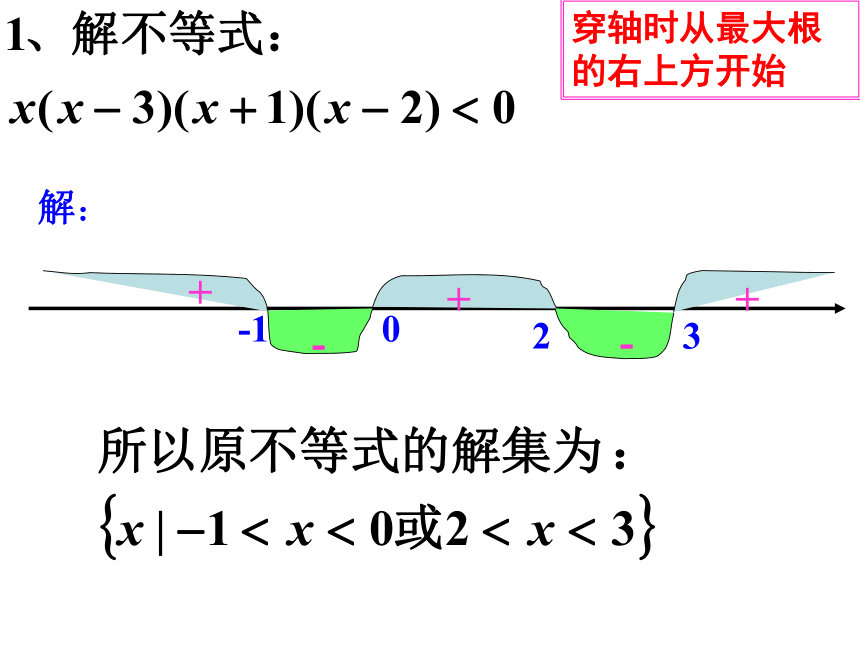
穿轴时从最大根
的右上方开始
一、数轴穿根法
对于解高次不等式常用“数轴标根法”
(变形→标根→穿线→定解)
解题步骤:
①如对于不等式f(x)>0;
②将f(x)分解为若干一次因式的乘积
(使各括号内x的系数为正),
再将各根由小到大有序的标在数轴上;
③从x轴右上方起,利用“幂指数的次数奇过偶不过”的原则求解不等式.
解:
-1
0
2
3
+
+
+
-
-
穿轴时从最大根
的右上方开始
0
2
-1
-3
x
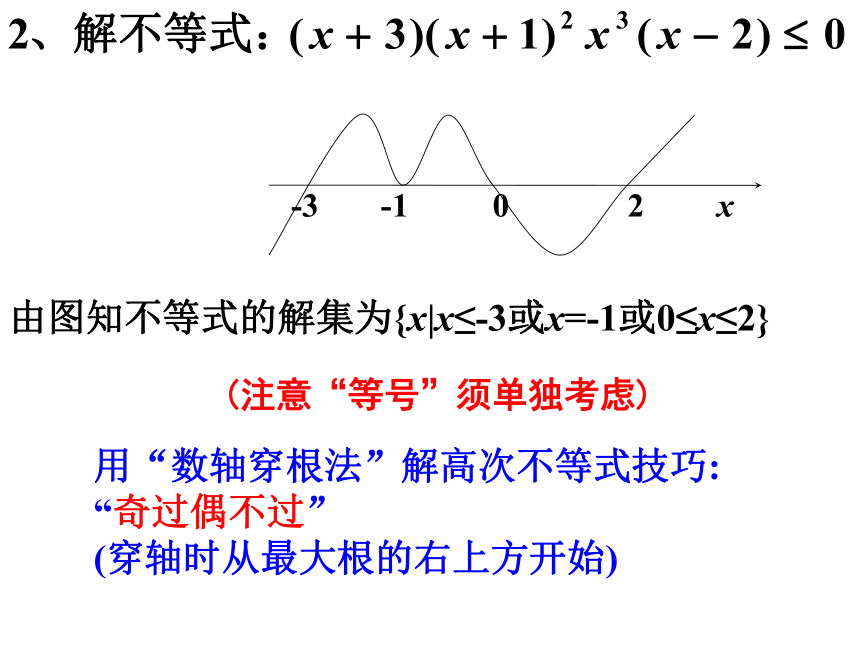
(注意“等号”须单独考虑)
用“数轴穿根法”解高次不等式技巧:
“奇过偶不过”
(穿轴时从最大根的右上方开始)
由图知不等式的解集为{x|x≤-3或x=-1或0≤x≤2}
由图知不等式的解集为{x|-1分式不等式的解法
一、分式不等式的定义
型如 叫分式不等式
其中
解分式不等式重要的是等价转化,
尤其是含“≥”或“≤”转换。
二、分式不等式的解法
主导思想:分式不等式转化为整式不等式
移项通分,分子分母因式分解,x的系数化为正,用穿轴法求结果
对于“等号”要谨慎处理
例:解不等式:
解:原不等式可化为:
且
得解集为:
解分式不等式时,一般不能去分母,
但分母恒为正或恒为负时可去分母。
分式不等式的解题思路:
先移项使右边为0,
再通分并将分子分母分解因式,
并使每一个因式中最高次项的系数为正,
最后用标根法求解。
注意:
x
-1
1
2
3
穿轴时从最大根的
右上方开始
解:原不等式等价于(x+1)(x-1)(x-2)(x-3)<0,将方程(x+1)(x-1)(x-2)(x-3)=0的根-1,1,2,3标在数轴上,从右到左画出示意图,
∴原不等式的解集是{x|-11
2
3
4
+
+
+
-
-
练习:
三、指数、对数不等式
转化时把握“同底数原则”“单调性原则”,
同时还要注意真数大于零,底数要使不等式有意义.
数轴标根法
复习:解一元二次不等式的一般步骤
(1)对不等式变形,使一端为零且二次项系数大于零;
(2)计算相应的判别式;
(3)当△>0时,求出相应的一元二次方程的两个根;
(5)根据函数图像写出一元二次不等式的解集。
(4)画出相应二次函数的草图;
记忆口诀: (前提a>0).
大于取两边,小于取中间
例:解不等式:
分析:
x的取
值范围
-3
4
-2
例:解不等式:
数轴标根法
穿轴时从最大根
的右上方开始
一、数轴穿根法
对于解高次不等式常用“数轴标根法”
(变形→标根→穿线→定解)
解题步骤:
①如对于不等式f(x)>0;
②将f(x)分解为若干一次因式的乘积
(使各括号内x的系数为正),
再将各根由小到大有序的标在数轴上;
③从x轴右上方起,利用“幂指数的次数奇过偶不过”的原则求解不等式.
解:
-1
0
2
3
+
+
+
-
-
穿轴时从最大根
的右上方开始
0
2
-1
-3
x
(注意“等号”须单独考虑)
用“数轴穿根法”解高次不等式技巧:
“奇过偶不过”
(穿轴时从最大根的右上方开始)
由图知不等式的解集为{x|x≤-3或x=-1或0≤x≤2}
由图知不等式的解集为{x|-1
一、分式不等式的定义
型如 叫分式不等式
其中
解分式不等式重要的是等价转化,
尤其是含“≥”或“≤”转换。
二、分式不等式的解法
主导思想:分式不等式转化为整式不等式
移项通分,分子分母因式分解,x的系数化为正,用穿轴法求结果
对于“等号”要谨慎处理
例:解不等式:
解:原不等式可化为:
且
得解集为:
解分式不等式时,一般不能去分母,
但分母恒为正或恒为负时可去分母。
分式不等式的解题思路:
先移项使右边为0,
再通分并将分子分母分解因式,
并使每一个因式中最高次项的系数为正,
最后用标根法求解。
注意:
x
-1
1
2
3
穿轴时从最大根的
右上方开始
解:原不等式等价于(x+1)(x-1)(x-2)(x-3)<0,将方程(x+1)(x-1)(x-2)(x-3)=0的根-1,1,2,3标在数轴上,从右到左画出示意图,
∴原不等式的解集是{x|-1
2
3
4
+
+
+
-
-
练习:
三、指数、对数不等式
转化时把握“同底数原则”“单调性原则”,
同时还要注意真数大于零,底数要使不等式有意义.
