3.3.1二元一次不等式表示平面区域-人教A版高中数学必修五课件(28张PPT)
文档属性
| 名称 | 3.3.1二元一次不等式表示平面区域-人教A版高中数学必修五课件(28张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 675.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览







文档简介
x
y
o
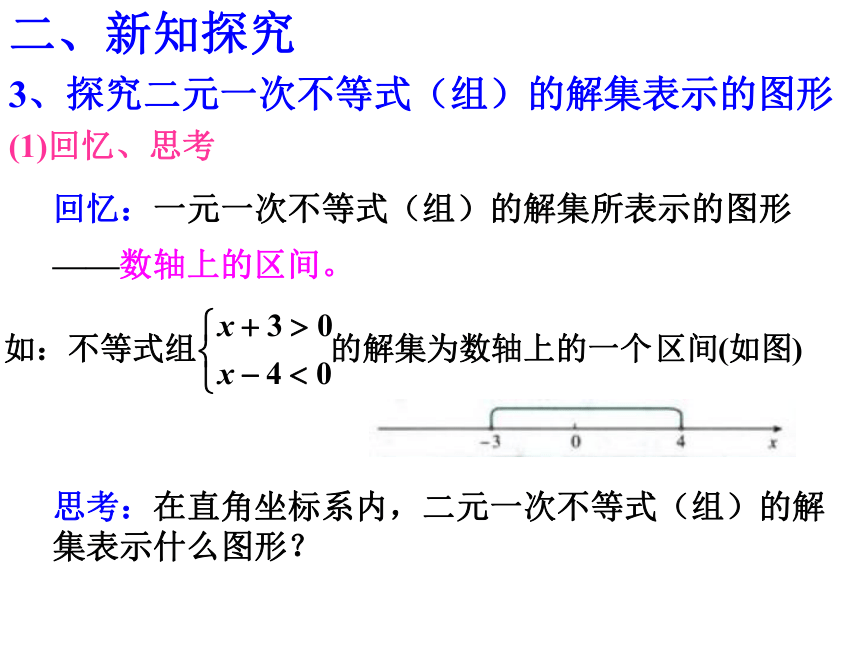
二元一次不等式(组)与简单线性规划问题
二元一次不等式(组)与平面区域
一、例题引入
一家银行的信贷部计划年初投入25000000元用于企业和个人贷款,希望这笔资金至少可带来30000元的收益,其中从企业信贷中获益12%,从个人贷款中获益10%。那么,信贷部如何分配资金呢?
问题:应该用什么不等式模型来刻画呢?
二、新知探究
1、建立二元一次不等式模型
(1)把实际问题转化为数学问题:
设企业信贷x元,个人贷款y元。
(2)把文字语言转化为符号语言:
投入25000000元
至少30000元的收益,信贷中获益12%,个人贷款中获益10%
(3)抽象出数学模型:
资金分配方式应满足的条件:
2、二元一次不等式和二元一次不等式组的定义
(1)二元一次不等式:
含有两个未知数,并且未知数的最高次数是1的不等式;
(2)二元一次不等式组:
由几个二元一次不等式组成的不等式组;
(3)二元一次不等式(组)的解集:
满足二元一次不等式(组)的有序实数对(x,y)构成的集合;
(4)有序数对可以看成直角坐标平面内点的坐标.
二、新知探究
二元一次不等式(组)的解集可以看成是直角坐标系内的点构成的集合。
3、探究二元一次不等式(组)的解集表示的图形
(1)回忆、思考
回忆:一元一次不等式(组)的解集所表示的图形
——数轴上的区间。
思考:在直角坐标系内,二元一次不等式(组)的解集表示什么图形?
二、新知探究
(2)探究
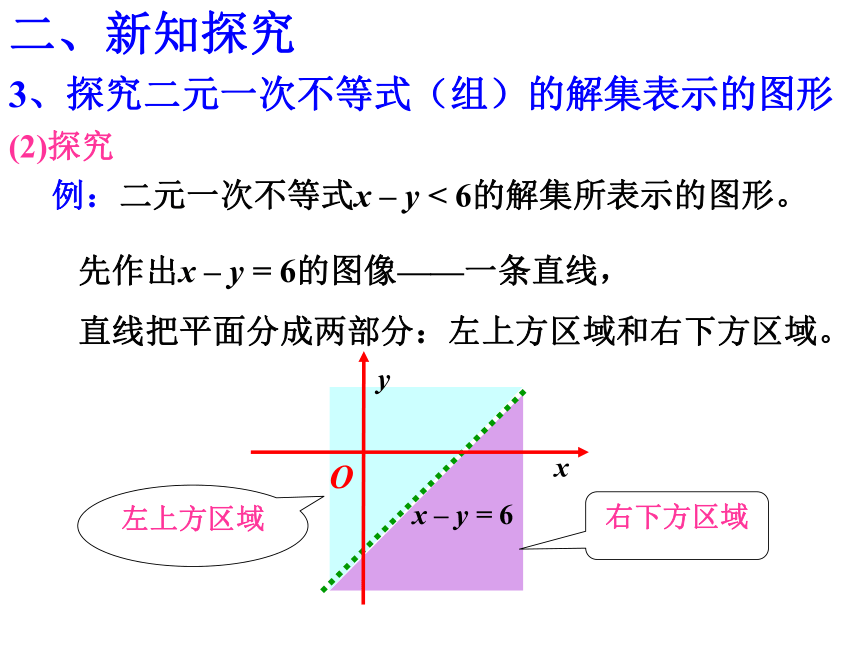
例:二元一次不等式x – y < 6的解集所表示的图形。
先作出x – y = 6的图像——一条直线,
直线把平面分成两部分:左上方区域和右下方区域。
O
x
y
x – y = 6
左上方区域
右下方区域
二、新知探究
3、探究二元一次不等式(组)的解集表示的图形
O
x
y
x – y = 6
O
x
y
x – y = 6
不等式x – y < 6表示直线
x – y = 6左上方的平面区域;
不等式x – y > 6表示直线
x – y = 6右下方的平面区域;
直线叫做这两个区域的边界。
把直线画成虚线,以表示区域不包括边界.
左上方区域
x – y < 6
O
x
y
x – y = 6
右下方区域
x – y > 6
二、新知探究
3、探究二元一次不等式(组)的解集表示的图形
二元一次不等式表示的平面区域
O
x
y
1
1
x+y-1=0
结论:
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域;
Ax+By+C<0表示的是另一侧的平面区域。
(虚线表示区域不包括边界直线)
x+y-1>0
x+y-1<0
判断二元一次不等式表示哪一侧平面区域的方法
O
x
y
1
1
x+y-1=0
x+y-1>0
x+y-1<0
由于对在直线Ax+By+C=0同一侧所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得的实数的符号都相同,故只需在这条直线的某一侧取一特殊点(x0,y0)以Ax0+By0+C的正负的情况便可判断Ax+By+C>0表示这一直线哪一侧的平面区域.
特殊地,当C≠0时常把原点作为此特殊点
直线定界,特殊点定域。
应该注意的几个问题:
1.若不等式中不含0,则边界应画成虚线,否则应画成实线
2.画图时应非常准确,否则将得不到正确结果
例1 画出不等式2x+y-6<0表示的平面区域。
O
x
y
3
6
2x+y-6=0
归纳:画二元一次不等式表示的平面区域常采用“直线定界,特殊点定域”的方法。特殊地,当C≠0时,常把原点作为此特殊点.
注意:把直线画成虚线以表示区域不包括边界
课堂练习1:
(1)画出不等式4x-3y≤12
表示的平面区域
x
y
4x-3y-12=0
x
y
x=1
(2)画出不等式x≥1
表示的平面区域
(1)x-y+1>0
练习:画出下列不等式所表示的平面区域。
(2)-2≤y≤1
(3)-x+3y+5<0
例2: 写出下图所表示的平面区域的二元一次不等式.
练习. 写出下图所表示的平面区域的二元一次不等式.
课本P86中1,2练习
复习
1.二元一次不等式的一般形式;
2.二元一次不等式表示的平面区域;
3.平面区域的画法及判断方法
画线定界
选点定域
热身练习
1.若不等式2x+y+m<3表示的平面区域包括点(0,0)和(1,1),则m的取值范围是:
2 .若点(1,3)和(-4,2)在直线
2x+y+m=0的两侧,则m的取值范围是:
(–∞,0)
(–5,6)
例1:用平面区域表示不等式组 的解集。
←
练习 :画出下列不等式组表示的平面区域
注:画图应非常准确,否则可能得不到正确结果。
C
练习
例2 、要将两种大小不同的钢板截成ABC三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
A规格
B规格
C规格
第一种钢板
2
1
1
第二种钢板
1
2
3
规格类型
钢板类型
今需要A、B、C三种规格的成品分别为15,18,27块,请用数学关系式和图形表示上述要求。
解:设需要截第一种钢板x张,第二种钢板y张,则
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
2
4
6
8
10
12
14
16
18
X+2y=18
X+3y=27
2x+y=15
2x+y≥15
x+2y≥18
x+3y ≥27
x ≥0
y ≥0
归纳解题思路:
1、设未知量;
2、列不等式关系
3、画出相应区域
例3、一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18t;生产1车皮乙种肥料需要的主要原料是磷酸盐1t,硝酸盐15t。现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式,并画出相应的平面区域。
解:设x,y分别为计划生产甲、乙两种混合肥料的车皮数,于是满足以下条件
4x+y=10
18x+15y =66
0
x
4x+y≤10
18x+15y ≤66
x≥0
y ≥0
y
练习:P86 第3、4题
例4.画出不等式组 所表示的平面区域,并求该区域面积。
x-y+2=0
x+2y-1=0
2x+y-5=0
A
B
C
y
o
二元一次不等式(组)与简单线性规划问题
二元一次不等式(组)与平面区域
一、例题引入
一家银行的信贷部计划年初投入25000000元用于企业和个人贷款,希望这笔资金至少可带来30000元的收益,其中从企业信贷中获益12%,从个人贷款中获益10%。那么,信贷部如何分配资金呢?
问题:应该用什么不等式模型来刻画呢?
二、新知探究
1、建立二元一次不等式模型
(1)把实际问题转化为数学问题:
设企业信贷x元,个人贷款y元。
(2)把文字语言转化为符号语言:
投入25000000元
至少30000元的收益,信贷中获益12%,个人贷款中获益10%
(3)抽象出数学模型:
资金分配方式应满足的条件:
2、二元一次不等式和二元一次不等式组的定义
(1)二元一次不等式:
含有两个未知数,并且未知数的最高次数是1的不等式;
(2)二元一次不等式组:
由几个二元一次不等式组成的不等式组;
(3)二元一次不等式(组)的解集:
满足二元一次不等式(组)的有序实数对(x,y)构成的集合;
(4)有序数对可以看成直角坐标平面内点的坐标.
二、新知探究
二元一次不等式(组)的解集可以看成是直角坐标系内的点构成的集合。
3、探究二元一次不等式(组)的解集表示的图形
(1)回忆、思考
回忆:一元一次不等式(组)的解集所表示的图形
——数轴上的区间。
思考:在直角坐标系内,二元一次不等式(组)的解集表示什么图形?
二、新知探究
(2)探究
例:二元一次不等式x – y < 6的解集所表示的图形。
先作出x – y = 6的图像——一条直线,
直线把平面分成两部分:左上方区域和右下方区域。
O
x
y
x – y = 6
左上方区域
右下方区域
二、新知探究
3、探究二元一次不等式(组)的解集表示的图形
O
x
y
x – y = 6
O
x
y
x – y = 6
不等式x – y < 6表示直线
x – y = 6左上方的平面区域;
不等式x – y > 6表示直线
x – y = 6右下方的平面区域;
直线叫做这两个区域的边界。
把直线画成虚线,以表示区域不包括边界.
左上方区域
x – y < 6
O
x
y
x – y = 6
右下方区域
x – y > 6
二、新知探究
3、探究二元一次不等式(组)的解集表示的图形
二元一次不等式表示的平面区域
O
x
y
1
1
x+y-1=0
结论:
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域;
Ax+By+C<0表示的是另一侧的平面区域。
(虚线表示区域不包括边界直线)
x+y-1>0
x+y-1<0
判断二元一次不等式表示哪一侧平面区域的方法
O
x
y
1
1
x+y-1=0
x+y-1>0
x+y-1<0
由于对在直线Ax+By+C=0同一侧所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得的实数的符号都相同,故只需在这条直线的某一侧取一特殊点(x0,y0)以Ax0+By0+C的正负的情况便可判断Ax+By+C>0表示这一直线哪一侧的平面区域.
特殊地,当C≠0时常把原点作为此特殊点
直线定界,特殊点定域。
应该注意的几个问题:
1.若不等式中不含0,则边界应画成虚线,否则应画成实线
2.画图时应非常准确,否则将得不到正确结果
例1 画出不等式2x+y-6<0表示的平面区域。
O
x
y
3
6
2x+y-6=0
归纳:画二元一次不等式表示的平面区域常采用“直线定界,特殊点定域”的方法。特殊地,当C≠0时,常把原点作为此特殊点.
注意:把直线画成虚线以表示区域不包括边界
课堂练习1:
(1)画出不等式4x-3y≤12
表示的平面区域
x
y
4x-3y-12=0
x
y
x=1
(2)画出不等式x≥1
表示的平面区域
(1)x-y+1>0
练习:画出下列不等式所表示的平面区域。
(2)-2≤y≤1
(3)-x+3y+5<0
例2: 写出下图所表示的平面区域的二元一次不等式.
练习. 写出下图所表示的平面区域的二元一次不等式.
课本P86中1,2练习
复习
1.二元一次不等式的一般形式;
2.二元一次不等式表示的平面区域;
3.平面区域的画法及判断方法
画线定界
选点定域
热身练习
1.若不等式2x+y+m<3表示的平面区域包括点(0,0)和(1,1),则m的取值范围是:
2 .若点(1,3)和(-4,2)在直线
2x+y+m=0的两侧,则m的取值范围是:
(–∞,0)
(–5,6)
例1:用平面区域表示不等式组 的解集。
←
练习 :画出下列不等式组表示的平面区域
注:画图应非常准确,否则可能得不到正确结果。
C
练习
例2 、要将两种大小不同的钢板截成ABC三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
A规格
B规格
C规格
第一种钢板
2
1
1
第二种钢板
1
2
3
规格类型
钢板类型
今需要A、B、C三种规格的成品分别为15,18,27块,请用数学关系式和图形表示上述要求。
解:设需要截第一种钢板x张,第二种钢板y张,则
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
2
4
6
8
10
12
14
16
18
X+2y=18
X+3y=27
2x+y=15
2x+y≥15
x+2y≥18
x+3y ≥27
x ≥0
y ≥0
归纳解题思路:
1、设未知量;
2、列不等式关系
3、画出相应区域
例3、一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18t;生产1车皮乙种肥料需要的主要原料是磷酸盐1t,硝酸盐15t。现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式,并画出相应的平面区域。
解:设x,y分别为计划生产甲、乙两种混合肥料的车皮数,于是满足以下条件
4x+y=10
18x+15y =66
0
x
4x+y≤10
18x+15y ≤66
x≥0
y ≥0
y
练习:P86 第3、4题
例4.画出不等式组 所表示的平面区域,并求该区域面积。
x-y+2=0
x+2y-1=0
2x+y-5=0
A
B
C
