3.3.2简单的线性规划问题-人教A版高中数学必修五课件(34张PPT)
文档属性
| 名称 | 3.3.2简单的线性规划问题-人教A版高中数学必修五课件(34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览







文档简介
3.3.2 简单的线性规划问题
一、引入
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
按甲、乙两种产品分别生产x、y件,由已知条件可得二元一次不等式组
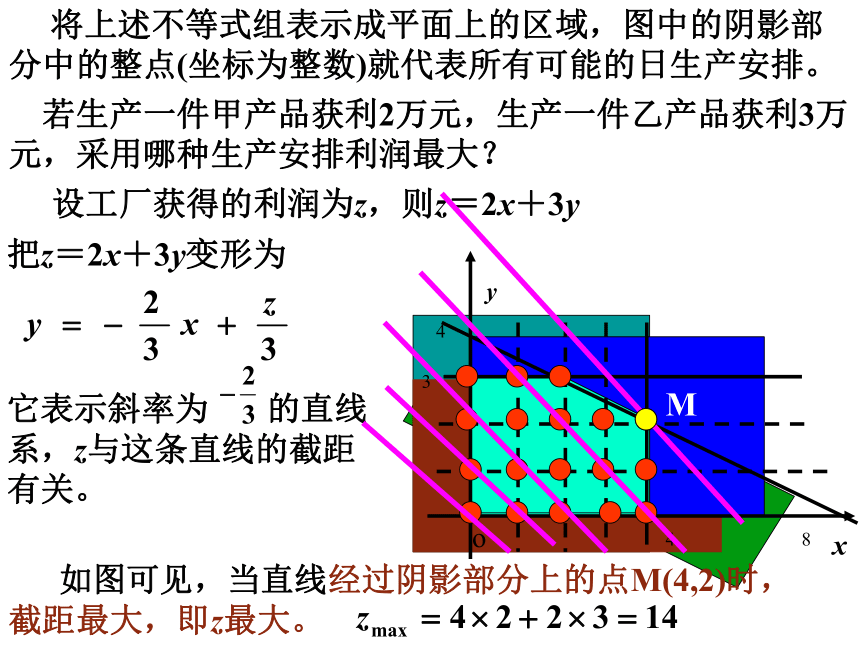
将上述不等式组表示成平面上的区域,图中的阴影部分中的整点(坐标为整数)就代表所有可能的日生产安排。
y
x
4
8
4
3
o
若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
设工厂获得的利润为z,则z=2x+3y
把z=2x+3y变形为
它表示斜率为 的直线系,z与这条直线的截距有关。
如图可见,当直线经过阴影部分上的点M(4,2)时,截距最大,即z最大。
M
二、基本概念
把求最大值或求最小值的函数称为目标函数,因为它是关于变量x、y的一次解析式,又称线性目标函数。
满足线性约束的解(x,y)叫做可行解。
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
一组关于变量x、y的一次不等式,称为线性约束条件。
由所有可行解组成的集合叫做可行域。
使目标函数取得最大值或最小值的可行解叫做这个问题的最优解。
A
B
C
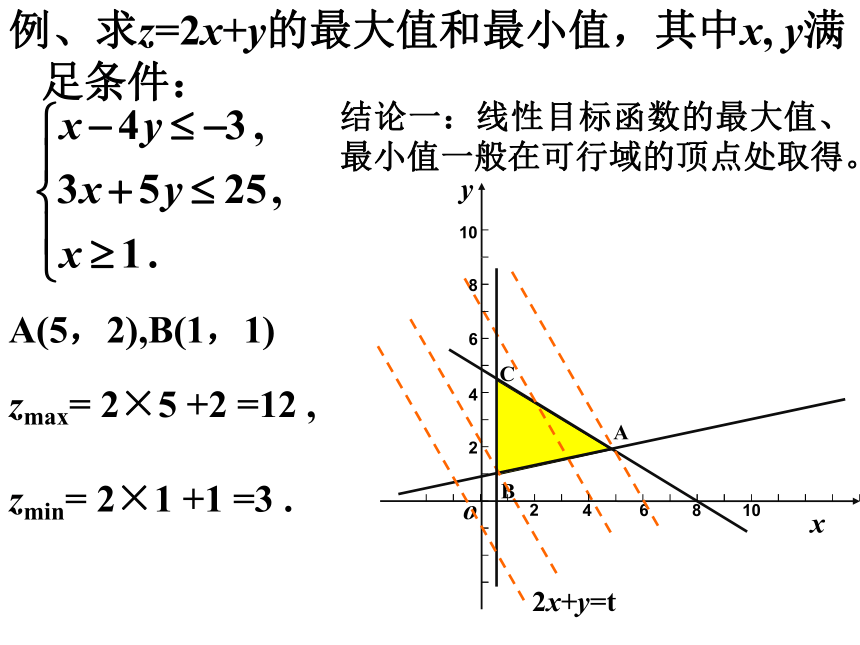
例、求z=2x+y的最大值和最小值,其中x, y满足条件:
10
8
6
2
4
2
o
6
8
10
4
x
y
2x+y=t
结论一:线性目标函数的最大值、最小值一般在可行域的顶点处取得。
A(5,2),B(1,1)
zmax= 2×5 +2 =12 ,
zmin= 2×1 +1 =3 .
解:如图作出以上不等式组所表示的可行域,
作直线l:2x+y=0,把直线l向右上方平移到过可行域上的点B时,z取最小值;
把l平移到过点A时,z取最大值.
∴z max = 2×5+2=12;
z min=2×1+1=3.
解线性规划问题的步骤:
(2)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解;
(4)答:作出答案。
(1)画:画出线性约束条件所表示的可行域;
B
A
C
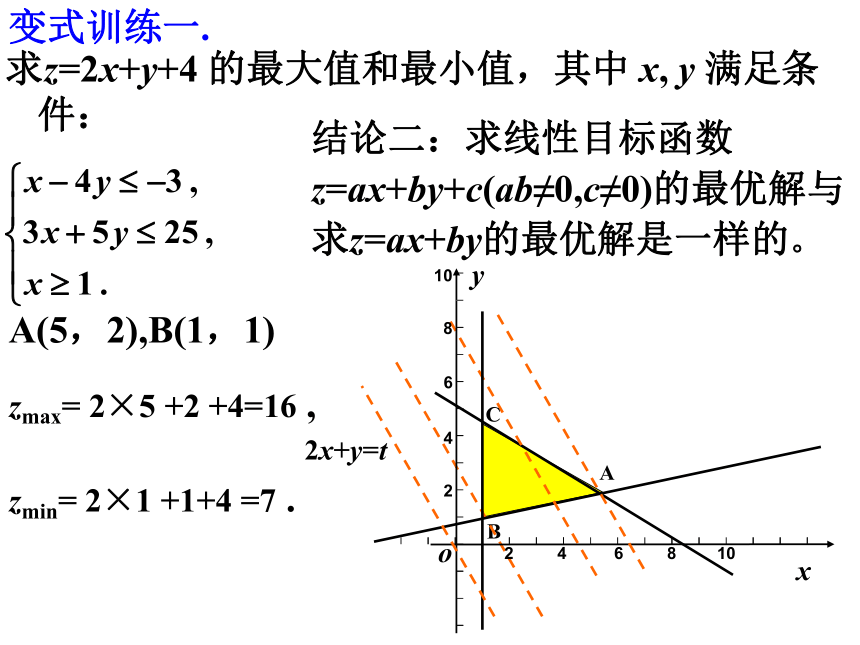
求z=2x+y+4 的最大值和最小值,其中 x, y 满足条件:
o
2
4
6
2
10
8
6
8
10
4
x
y
2x+y=t
结论二:求线性目标函数z=ax+by+c(ab≠0,c≠0)的最优解与求z=ax+by的最优解是一样的。
A(5,2),B(1,1)
zmax= 2×5 +2 +4=16 ,
zmin= 2×1 +1+4 =7 .
变式训练一.
B
2
4
6
8
10
2
o
6
8
10
4
x
y
A
C
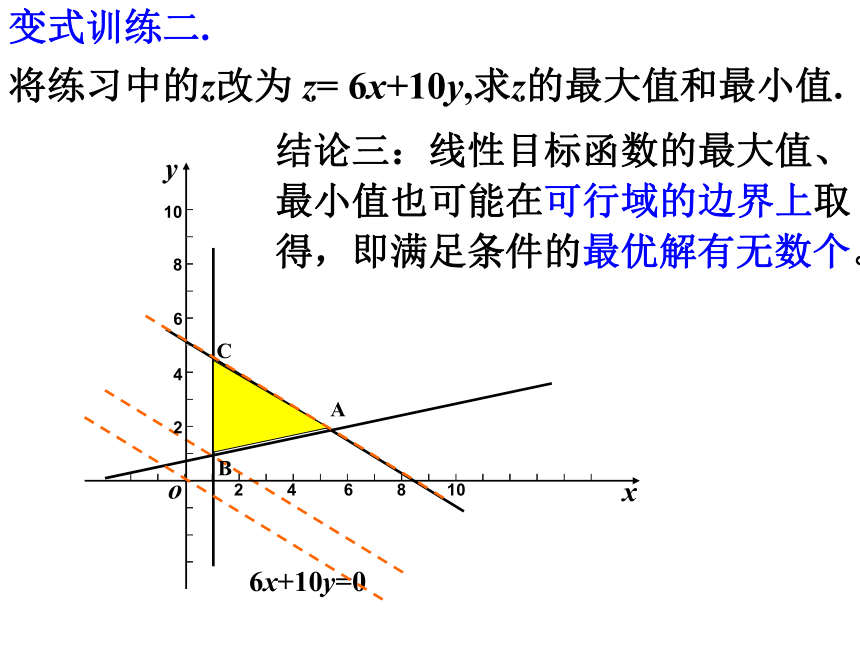
变式训练二.
将练习中的z改为 z= 6x+10y,求z的最大值和最小值.
6x+10y=0
结论三:线性目标函数的最大值、最小值也可能在可行域的边界上取得,即满足条件的最优解有无数个。
练习:已知平面区域如右图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m的值为______
B
4
2
o
2
8
10
6
6
8
10
4
x
y
A
C
2x-y=0
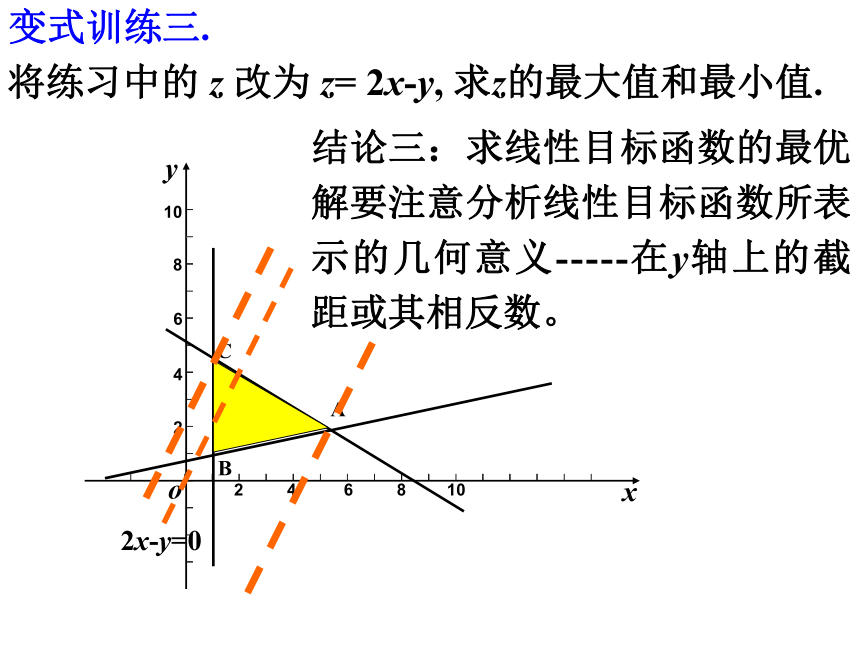
变式训练三.
将练习中的 z 改为 z= 2x-y, 求z的最大值和最小值.
结论三:求线性目标函数的最优解要注意分析线性目标函数所表示的几何意义-----在y轴上的截距或其相反数。
1.若 则目标函数z=x+2y的取值范围是
[2,6]
2.若 则目标函数k=2x-y的最大值是
作业: P91练习第一题
求目标函数z=ax+by(a,b为常数)在线性约束条件下的最大值,最小值问题。
转化
小结:
解题步骤:
(1)画;(2)移;(3)求;(4)答
y张
A规格
B规格
C规格
第一种钢板
2
1
1
第二种钢板
1
2
3
规格类型
钢板类型
例题分析
例2:要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 :
解:设需截第一种钢板x张,
第二种钢板y张,则
今需要A,B,C三种规格的成品分别为15,18,27块,
问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。
x张
目标函数为 z=x+y
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y =0
作出一组平行直线z=x+y,
目标函数z= x+y
B(3,9)
C(4,8)
当直线经过点A时z=x+y=11.4,
x+y=12
调整优值法
2
4
6
18
12
8
27
2
4
6
8
10
15
但它不是最优整数解.
作直线x+y=12,
解得B(3,9)和C(4,8)
直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解.
A(18/5,39/5)
A(18/5,39/5)
作出可行域(如图)
网格线法
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y=0
经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.
答:(略)
作出一组平行直线t = x+y,
目标函数
z=x+y
B(3,9)
C(4,8)
A(18/5,39/5)
打网格线法
在可行域内打出网格线,
当直线经过点A时t=x+y=11.4,但它不是最优整数解,
将直线x+y=11.4继续向上平移,
7.5
15
18
27
9
即先求非整数条件下的最优解,调整z的值使不定方程Ax+By=z存在最大(小)的整点值,最后筛选出整点最优解.
线性规划求最优整数解的一般方法:
1.调整优解法:
结论:
即先打网格,描出可行域内的整点,平移直线,最先经过或最后经过的整点坐标即为最优整解.
2.打网格线法:
【思路点拨】 根据题意设出午餐和晚餐的单位数,以此
表示出所花的费用,用线性规划求所花费用的最小值.
例3、某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
解:设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,
所花的费用为z元,则依题意得:
z=2.5x+4y,且x,y满足
如图所示,作出可行域:
不等式组 表示的平面区域内的整数点共有___个
巩固练习1:
1 2 3 4 x
y
4
3
2
1
0
4x+3y=12
3
在可行域内找出最优解、线性规划整数解问题的一般方法是:
1.若区域“顶点”处恰好为整点,那么它就是最优解;
(在包括边界的情况下)
2.若区域“顶点”不是整点或不包括边界时,应先求出该点坐标,并计算目标函数值z,然后在可行域内适当放缩目标函数值,使它为整数,且与z最接近,在这条对应的直线中,取可行域内整点,如果没有整点,继续放缩,直至取到整点为止。
3.在可行域内找整数解,一般采用平移找解法,找整点、平移直线、找出整数最优解
有关二元一次代数式取值范围
解:由①、②同向相加可得:
③
求2x+y的取值范围。
例1.若实数 x,y满足
①
②
由②得
将上式与①同向相加得
④
③+④得
以上解法正确吗?为什么?
首先:我们画出
表示的平面区域
当x=3,y=0时,得出2x+y的最小值为6,但此时x+y=3,点(3,0)不在不等式组的所表示的平面区域内,所以上述解答明显错了.
1
2
3
4
5
6
7
x
6
5
4
3
2
1
0
-1
-1
-2
y
-2
-3
-4
A
D
C
B
从图中我们可以看出
没错
解得
实际上扩大了许多
通过分析,我们知道上述解法中,
是对的,但用x的最大(小)值及y的最大(小)值来确定2x+y的最大(小)值却是不合理的。
怎么来解决这个问题和这一类问题呢?这就是我们今天要学习的线性规划问题。
求2x+y的取值范围。
例1.若实数 x,y满足
①
②
y
1
2
3
4
5
6
7
x
6
5
4
3
2
1
0
-1
-1
-2
-2
-3
-4
A
D
C
B
我们设z=2x+y方程变形为y=-2x+z,等式表示斜率为-2,纵截距为z的直线,把z看成参数,方程表示的是一组平行线.
要求z的范围,可转化为求这一组平行线中,与阴影区域有交点,且在y轴上的截距达到最大和最小的直线.
?
所以
解法2:由待定系数法:
∴7≤2x+y≤11
∵4≤x+y≤6,2≤x-y≤4
∴ 2x+y=3/2×(x+y)+ 1/2 × (x-y )
m=3/2 ,n=1/2
∴m+n =2,m-n =1
= (m+n)x + (m-n) y
设 2x+y= m(x+y) + n(x-y)
求x+3y的最小值和最大值。
练习.若实数 x,y满足
二元一次不等式
表示平面区域
直线定界,
特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:画、移、求、答
小结:
作业:P93 A组 4
【答案】 1
【答案】 C
一、引入
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
按甲、乙两种产品分别生产x、y件,由已知条件可得二元一次不等式组
将上述不等式组表示成平面上的区域,图中的阴影部分中的整点(坐标为整数)就代表所有可能的日生产安排。
y
x
4
8
4
3
o
若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
设工厂获得的利润为z,则z=2x+3y
把z=2x+3y变形为
它表示斜率为 的直线系,z与这条直线的截距有关。
如图可见,当直线经过阴影部分上的点M(4,2)时,截距最大,即z最大。
M
二、基本概念
把求最大值或求最小值的函数称为目标函数,因为它是关于变量x、y的一次解析式,又称线性目标函数。
满足线性约束的解(x,y)叫做可行解。
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
一组关于变量x、y的一次不等式,称为线性约束条件。
由所有可行解组成的集合叫做可行域。
使目标函数取得最大值或最小值的可行解叫做这个问题的最优解。
A
B
C
例、求z=2x+y的最大值和最小值,其中x, y满足条件:
10
8
6
2
4
2
o
6
8
10
4
x
y
2x+y=t
结论一:线性目标函数的最大值、最小值一般在可行域的顶点处取得。
A(5,2),B(1,1)
zmax= 2×5 +2 =12 ,
zmin= 2×1 +1 =3 .
解:如图作出以上不等式组所表示的可行域,
作直线l:2x+y=0,把直线l向右上方平移到过可行域上的点B时,z取最小值;
把l平移到过点A时,z取最大值.
∴z max = 2×5+2=12;
z min=2×1+1=3.
解线性规划问题的步骤:
(2)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解;
(4)答:作出答案。
(1)画:画出线性约束条件所表示的可行域;
B
A
C
求z=2x+y+4 的最大值和最小值,其中 x, y 满足条件:
o
2
4
6
2
10
8
6
8
10
4
x
y
2x+y=t
结论二:求线性目标函数z=ax+by+c(ab≠0,c≠0)的最优解与求z=ax+by的最优解是一样的。
A(5,2),B(1,1)
zmax= 2×5 +2 +4=16 ,
zmin= 2×1 +1+4 =7 .
变式训练一.
B
2
4
6
8
10
2
o
6
8
10
4
x
y
A
C
变式训练二.
将练习中的z改为 z= 6x+10y,求z的最大值和最小值.
6x+10y=0
结论三:线性目标函数的最大值、最小值也可能在可行域的边界上取得,即满足条件的最优解有无数个。
练习:已知平面区域如右图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m的值为______
B
4
2
o
2
8
10
6
6
8
10
4
x
y
A
C
2x-y=0
变式训练三.
将练习中的 z 改为 z= 2x-y, 求z的最大值和最小值.
结论三:求线性目标函数的最优解要注意分析线性目标函数所表示的几何意义-----在y轴上的截距或其相反数。
1.若 则目标函数z=x+2y的取值范围是
[2,6]
2.若 则目标函数k=2x-y的最大值是
作业: P91练习第一题
求目标函数z=ax+by(a,b为常数)在线性约束条件下的最大值,最小值问题。
转化
小结:
解题步骤:
(1)画;(2)移;(3)求;(4)答
y张
A规格
B规格
C规格
第一种钢板
2
1
1
第二种钢板
1
2
3
规格类型
钢板类型
例题分析
例2:要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 :
解:设需截第一种钢板x张,
第二种钢板y张,则
今需要A,B,C三种规格的成品分别为15,18,27块,
问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。
x张
目标函数为 z=x+y
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y =0
作出一组平行直线z=x+y,
目标函数z= x+y
B(3,9)
C(4,8)
当直线经过点A时z=x+y=11.4,
x+y=12
调整优值法
2
4
6
18
12
8
27
2
4
6
8
10
15
但它不是最优整数解.
作直线x+y=12,
解得B(3,9)和C(4,8)
直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解.
A(18/5,39/5)
A(18/5,39/5)
作出可行域(如图)
网格线法
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y=0
经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.
答:(略)
作出一组平行直线t = x+y,
目标函数
z=x+y
B(3,9)
C(4,8)
A(18/5,39/5)
打网格线法
在可行域内打出网格线,
当直线经过点A时t=x+y=11.4,但它不是最优整数解,
将直线x+y=11.4继续向上平移,
7.5
15
18
27
9
即先求非整数条件下的最优解,调整z的值使不定方程Ax+By=z存在最大(小)的整点值,最后筛选出整点最优解.
线性规划求最优整数解的一般方法:
1.调整优解法:
结论:
即先打网格,描出可行域内的整点,平移直线,最先经过或最后经过的整点坐标即为最优整解.
2.打网格线法:
【思路点拨】 根据题意设出午餐和晚餐的单位数,以此
表示出所花的费用,用线性规划求所花费用的最小值.
例3、某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
解:设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,
所花的费用为z元,则依题意得:
z=2.5x+4y,且x,y满足
如图所示,作出可行域:
不等式组 表示的平面区域内的整数点共有___个
巩固练习1:
1 2 3 4 x
y
4
3
2
1
0
4x+3y=12
3
在可行域内找出最优解、线性规划整数解问题的一般方法是:
1.若区域“顶点”处恰好为整点,那么它就是最优解;
(在包括边界的情况下)
2.若区域“顶点”不是整点或不包括边界时,应先求出该点坐标,并计算目标函数值z,然后在可行域内适当放缩目标函数值,使它为整数,且与z最接近,在这条对应的直线中,取可行域内整点,如果没有整点,继续放缩,直至取到整点为止。
3.在可行域内找整数解,一般采用平移找解法,找整点、平移直线、找出整数最优解
有关二元一次代数式取值范围
解:由①、②同向相加可得:
③
求2x+y的取值范围。
例1.若实数 x,y满足
①
②
由②得
将上式与①同向相加得
④
③+④得
以上解法正确吗?为什么?
首先:我们画出
表示的平面区域
当x=3,y=0时,得出2x+y的最小值为6,但此时x+y=3,点(3,0)不在不等式组的所表示的平面区域内,所以上述解答明显错了.
1
2
3
4
5
6
7
x
6
5
4
3
2
1
0
-1
-1
-2
y
-2
-3
-4
A
D
C
B
从图中我们可以看出
没错
解得
实际上扩大了许多
通过分析,我们知道上述解法中,
是对的,但用x的最大(小)值及y的最大(小)值来确定2x+y的最大(小)值却是不合理的。
怎么来解决这个问题和这一类问题呢?这就是我们今天要学习的线性规划问题。
求2x+y的取值范围。
例1.若实数 x,y满足
①
②
y
1
2
3
4
5
6
7
x
6
5
4
3
2
1
0
-1
-1
-2
-2
-3
-4
A
D
C
B
我们设z=2x+y方程变形为y=-2x+z,等式表示斜率为-2,纵截距为z的直线,把z看成参数,方程表示的是一组平行线.
要求z的范围,可转化为求这一组平行线中,与阴影区域有交点,且在y轴上的截距达到最大和最小的直线.
?
所以
解法2:由待定系数法:
∴7≤2x+y≤11
∵4≤x+y≤6,2≤x-y≤4
∴ 2x+y=3/2×(x+y)+ 1/2 × (x-y )
m=3/2 ,n=1/2
∴m+n =2,m-n =1
= (m+n)x + (m-n) y
设 2x+y= m(x+y) + n(x-y)
求x+3y的最小值和最大值。
练习.若实数 x,y满足
二元一次不等式
表示平面区域
直线定界,
特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:画、移、求、答
小结:
作业:P93 A组 4
【答案】 1
【答案】 C
