4.3.1 对数的概念-【新教材】人教A版(2019)高中数学必修第一册课件(19张PPT)
文档属性
| 名称 | 4.3.1 对数的概念-【新教材】人教A版(2019)高中数学必修第一册课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 20:52:21 | ||
图片预览


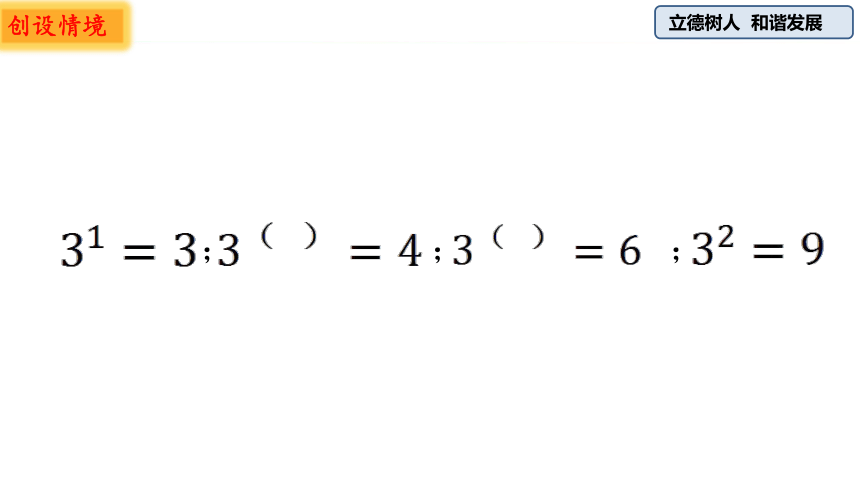




文档简介
4.3.1 对数的概念
第四章 指数函数与对数函数
在指数函数 中,当函数值分别取3,4,6,
9时,你能不能求出自变量x的值分别为多少?
创设情境
; ; ;
创设情境
在4.2.1的问题1中,通过指数幂运算,我们能从y= 中求出经过x年后B地景区的游客人次为2001年的y倍.反之,如果要求经过多少年游客人次是2001年的2倍,3倍,4倍,…,那么该如何解决?
上述问题实际上就是从2= ,3=
, 4= ,…中分别求出x,即已知底数和幂的值,求指数.用我们现有的知识体系可以解决上述问题吗?
这就是本节要学习的对数。
创设情境
对 数
对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年)。他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发明。恩格斯把对数的发明与解析几何的创始,微积分的建立并称为17世纪数学的三大成就。(具体发明的过程请大家阅读课本128页的对数的发明。)
对数的发明
对 数
对数表的发明,很快得到了人们的认可,尤其是天文学界,他们认为对数的发明延长了天文学者的寿命.伽利略甚至说,给他空间、时间及对数,他就可以创造一个宇宙.在生产生活中测量地震的里氏多少多少级,就是个对数;PH值是个对数;人口增长率、死亡率、生物的繁殖率,银行的利息率、国民经济增长率、原子的核衰变,甚至人死后的体温降低率等等等等.这些计算方面的问题,很多都要用到对数的.
对数的作用
注意:
(1)对数的写法;
(2)log只是记录对数的符号,类似于三角中的正余弦sin,cos等;
(3) logaN不是loga与N的乘积;
(4)对数是一个数,是指数式中指数的等价表达。
对数的概念
例如·,由于 ,所以x就是以1.11为底
2的对数,记作 ;
由于 ,所以x就是以3为底
6的对数,记作 ;
再如,由于 ,所以以4为底
16的对数是2,记作
2 = log4 16
对数的概念
常用对数与自然对数
lg N=
ln N=
log10 N
loge N
常见的对数
对数的概念
思考:为什么零和负数没有对数?
(指的是真数)
(真数N>0)
对数的基本性质
×
×
巩固训练
巩固训练
典例解析
其实指数式与对数式,虽然从形式上看,两者不同,
但本质上是一致的。这个一致就是底数、指数(对数)、
幂(真数)三者之间的关系。
归纳总结
典例解析
课堂小结
课后作业
作业本A
课本123页练习1,2,3(做在书上)
课本126页习题4.3 第2题
金版P86-P88
问题探究
第四章 指数函数与对数函数
在指数函数 中,当函数值分别取3,4,6,
9时,你能不能求出自变量x的值分别为多少?
创设情境
; ; ;
创设情境
在4.2.1的问题1中,通过指数幂运算,我们能从y= 中求出经过x年后B地景区的游客人次为2001年的y倍.反之,如果要求经过多少年游客人次是2001年的2倍,3倍,4倍,…,那么该如何解决?
上述问题实际上就是从2= ,3=
, 4= ,…中分别求出x,即已知底数和幂的值,求指数.用我们现有的知识体系可以解决上述问题吗?
这就是本节要学习的对数。
创设情境
对 数
对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年)。他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发明。恩格斯把对数的发明与解析几何的创始,微积分的建立并称为17世纪数学的三大成就。(具体发明的过程请大家阅读课本128页的对数的发明。)
对数的发明
对 数
对数表的发明,很快得到了人们的认可,尤其是天文学界,他们认为对数的发明延长了天文学者的寿命.伽利略甚至说,给他空间、时间及对数,他就可以创造一个宇宙.在生产生活中测量地震的里氏多少多少级,就是个对数;PH值是个对数;人口增长率、死亡率、生物的繁殖率,银行的利息率、国民经济增长率、原子的核衰变,甚至人死后的体温降低率等等等等.这些计算方面的问题,很多都要用到对数的.
对数的作用
注意:
(1)对数的写法;
(2)log只是记录对数的符号,类似于三角中的正余弦sin,cos等;
(3) logaN不是loga与N的乘积;
(4)对数是一个数,是指数式中指数的等价表达。
对数的概念
例如·,由于 ,所以x就是以1.11为底
2的对数,记作 ;
由于 ,所以x就是以3为底
6的对数,记作 ;
再如,由于 ,所以以4为底
16的对数是2,记作
2 = log4 16
对数的概念
常用对数与自然对数
lg N=
ln N=
log10 N
loge N
常见的对数
对数的概念
思考:为什么零和负数没有对数?
(指的是真数)
(真数N>0)
对数的基本性质
×
×
巩固训练
巩固训练
典例解析
其实指数式与对数式,虽然从形式上看,两者不同,
但本质上是一致的。这个一致就是底数、指数(对数)、
幂(真数)三者之间的关系。
归纳总结
典例解析
课堂小结
课后作业
作业本A
课本123页练习1,2,3(做在书上)
课本126页习题4.3 第2题
金版P86-P88
问题探究
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
