北师大版高中数学必修1-3.3.3 指数函数 课件(26张PPT)
文档属性
| 名称 | 北师大版高中数学必修1-3.3.3 指数函数 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 402.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 00:00:00 | ||
图片预览





文档简介
一.指数函数的定义:
一般地,形如 y =ax (a>0,且a≠1) 的函数叫做指数函数,其中 x是自变量.定义域是R .
指数函数
探究:为什么要规定
?
(1)若
则当x > 0时,
当x≤0时,
无意义.
在实数范围内函数值不存在.
(3)若
则对于任何
(2)若
则对于x的某些数值,可使
无意义.
如
,这时对于
……等等,
是一个常量,没有研究的必要性
例1.判断下列函数是否是指数函数:
注:指数函数的解析式 中 的系数是1
且指数位置仅有自变量 ???
练习:
1.下列函数是指数函数的是 ( )
A. y=(-3)x B. y=3x+1 C. y=-3x+1 D. y=3-x
2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求a的值.
解:由指数函数 的定义有
a2 - 3a + 3=1
a>0
a ≠ 1
∴ a = 2
a =1或a = 2
a>0
a≠1
解得
D
3.已知指数函数 的图象经过点 ,求
的值.
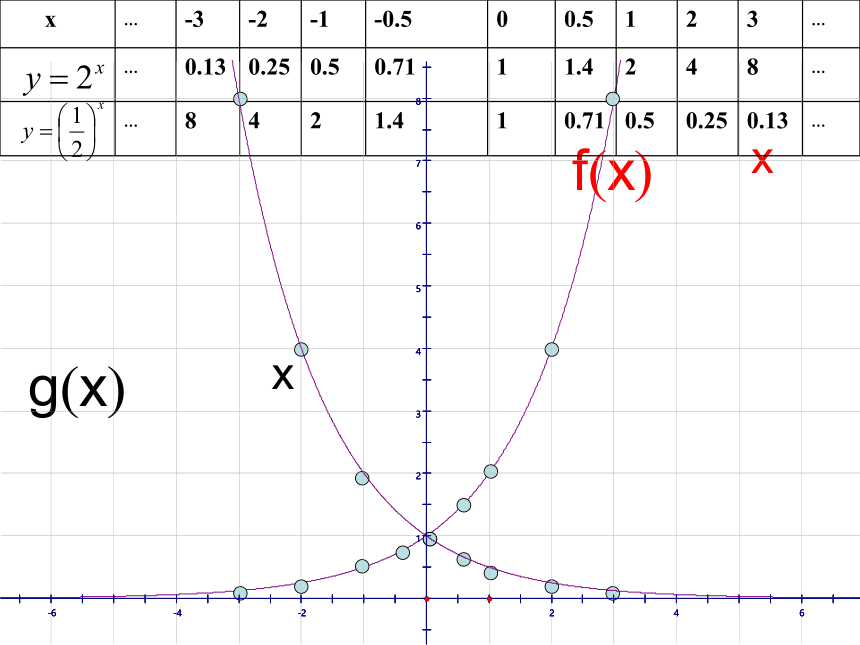
在同一坐标系中分别作出如下函数的图象:
与
与
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
( )
( )
x
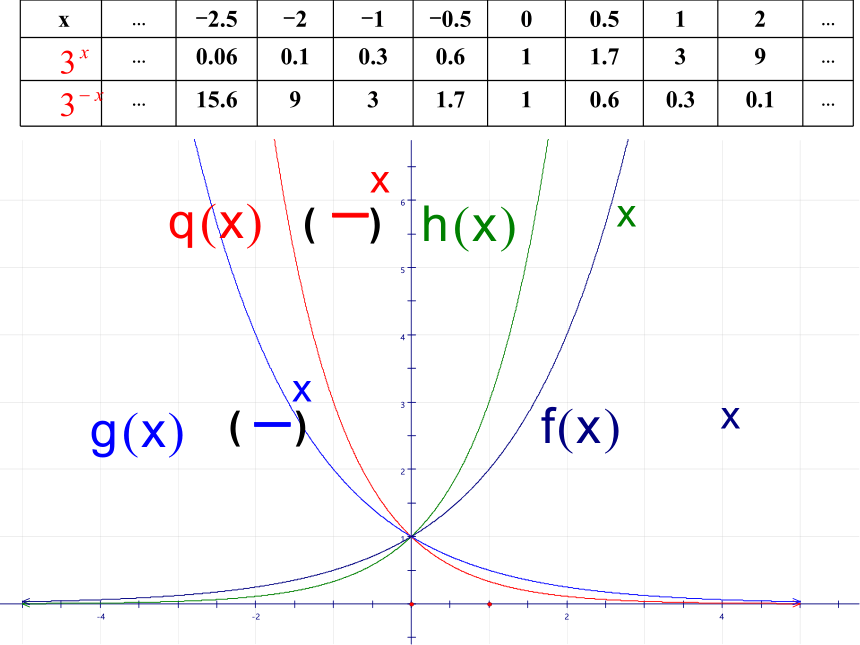
…
-2.5
-2
-1
-0.5
0
0.5
1
2
…
…
0.06
0.1
0.3
0.6
1
1.7
3
9
…
…
15.6
9
3
1.7
1
0.6
0.3
0.1
…
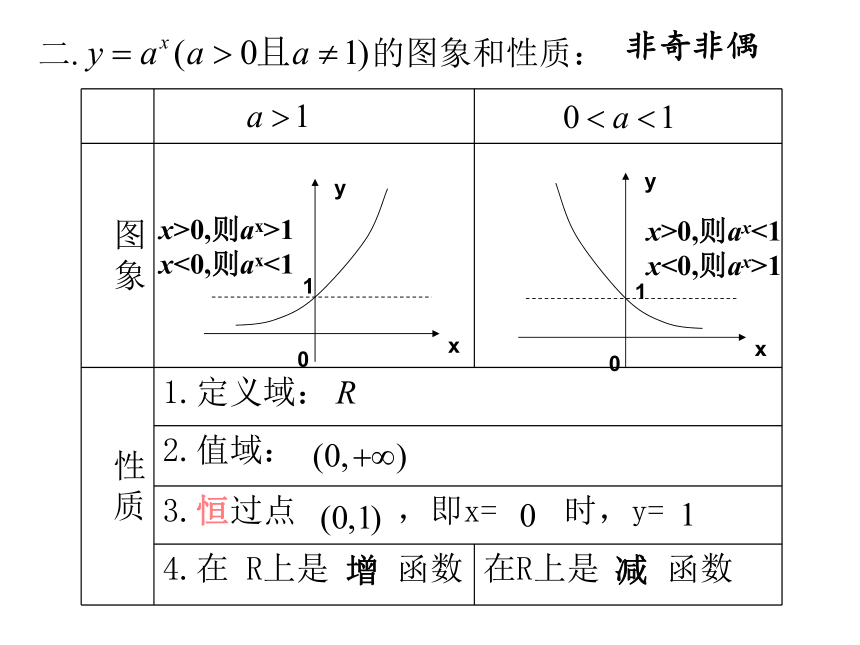
二. 的图象和性质:
图
象
性
质
1.定义域:
2.值域:
3.恒过点 ,即x= 时,y=
4.在 R上是 函数
在R上是 函数
x
y
0
1
x
y
0
1
增
减
x>0,则ax>1
x<0,则ax<1
x>0,则ax<1
x<0,则ax>1
非奇非偶
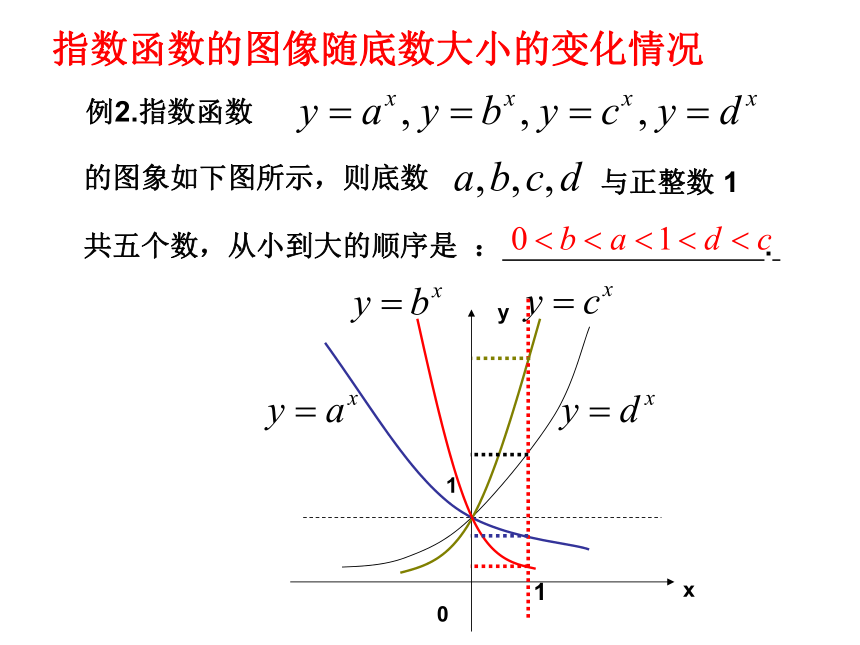
例2.指数函数
的图象如下图所示,则底数
与正整数 1
共五个数,从小到大的顺序是 : .
x
y
0
1
1
指数函数的图像随底数大小的变化情况
例3 、比较下列各题中两个值的大小:
①
,
解① :利用指数函数单调性
,
的底数是1.7,它们可以看成函数
当 x=2.5和3时的函数值;
因为1.7>1,所以函数
在R上是增函数,
x
y
0
1
而2.5<3,所以,
2.5
3
y=1.7x
构造函数y=1.7x
利用单调性比较两个数的大小
②
.
③
④
.
.
例3 、比较下列各题中两个值的大小:
练习:判断大小
三.利用指数函数单调性比大小的方法 :
2. 中间量法(搭桥比较法):
用特殊的数1或0等.
1.构造函数的方法:(包括可转化为同底的)
关于过定点的问题
例4.函数 的图象过定点 .
关键点:a0=1(a≠0)
例5.解不等式
解:由指数函数的单调性可得:
整理得:
原不等式的解集为:
解得:
解简单的指数不等式
练习:1.解下列不等式
①
思考:解不等式(a>0且a≠1)
②
2.求定义域
例6.求定义域、值域:
解:(1)由x-1≠0得x≠1所以,所求函数定义域为
{x|x≠1}
⑴
⑵
由 ,得y≠1
所以,所求函数值域为{y|y>0且y≠1}
求函数的定义域、值域
说明:对于值域的求解,可以令
考察指数函数y=
并结合图象直观地得到:
函数值域为{y|y>0且y≠1}
⑵
解:
由5x-1≥0得
所以,所求函数定义域为
由
得y≥1
所以,所求函数值域为{y|y≥1}
练习:
1.求下列函数的定义域和值域:
⑴
(3)
复合函数的单调性
例8. 讨论函数 的单调性
练习.求函数 的单调区间
和值域.
x
-3
-2
-1
0
1
2
3
0.125
0.25
0.5
1
2
4
8
0.25
0.5
1
2
4
8
16
0.5
1
2
4
8
16
32
例:在同一坐标系下作出下列函数的图象,并指出
它们与指数函数y= 的图象的关系,
与
与
⑴
⑵
解:⑴列出函数数据表,作出图像
专题:图象的变换
比较函数y=
、y=
与y=
的关系:
的图象向左平行移动1个单位长度,
的图象;
的图象向左平行
移动2个单位长
度,就得到函数
y=
的图象。
将指数函数y=
就得到函数y=
将指数函数y=
1
x
o
y
y=2x+1
y=2x+2
y=2x
x
比较函数y=
、y=
与y=
的关系:
的图象向右平行移动1个单位长度,
的图象;
的图象向右平行移动2
个单位长度,就得到函
数y=
的图象。
将指数函数y=
就得到函数y=
将指数函数y=
y
y=2x-1
y=2x-2
y=2x
x
x
o
小结:将函数y=f(x)的图像向左(a>0)或向右(a<0)平移∣a∣个单位,即得函数y=f(x+a)的图像。
例. 已知函数
作出函数图象,求定义域、
与
图象的关系。
值域,并探讨
解:
定义域:R 值域:
作出图象如下:
练习: 已知函数
,作出图象,求定义域、值域。
函 数
y=f(x)
y=f(x+a)
y=f(x)+a
y=f(-x)
y=-f(x)
y=-f(-x)
y=f(|x|)
y=|f(x)|
对于有些复合函数的图象,常用基本函数图象+变换作出:即把我们熟知的基本函数图象,通过平移、作其对称图等方法,得到我们所要求作的复合函数的图象,这种方法我们遇到的主要有以下几种形式:
a>0时向左平移a个单位;a<0时向右平移|a|个单位.
a>0时向上平移a个单位;a<0时向下平移|a|个单位.
y=f(-x)与y=f(x)的图象关于y轴对称.
y=-f(x)与y=f(x)的图象关于x轴对称.
y=-f(-x)与y=f(x)的图象关于原点轴对称.
一般地,形如 y =ax (a>0,且a≠1) 的函数叫做指数函数,其中 x是自变量.定义域是R .
指数函数
探究:为什么要规定
?
(1)若
则当x > 0时,
当x≤0时,
无意义.
在实数范围内函数值不存在.
(3)若
则对于任何
(2)若
则对于x的某些数值,可使
无意义.
如
,这时对于
……等等,
是一个常量,没有研究的必要性
例1.判断下列函数是否是指数函数:
注:指数函数的解析式 中 的系数是1
且指数位置仅有自变量 ???
练习:
1.下列函数是指数函数的是 ( )
A. y=(-3)x B. y=3x+1 C. y=-3x+1 D. y=3-x
2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求a的值.
解:由指数函数 的定义有
a2 - 3a + 3=1
a>0
a ≠ 1
∴ a = 2
a =1或a = 2
a>0
a≠1
解得
D
3.已知指数函数 的图象经过点 ,求
的值.
在同一坐标系中分别作出如下函数的图象:
与
与
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
( )
( )
x
…
-2.5
-2
-1
-0.5
0
0.5
1
2
…
…
0.06
0.1
0.3
0.6
1
1.7
3
9
…
…
15.6
9
3
1.7
1
0.6
0.3
0.1
…
二. 的图象和性质:
图
象
性
质
1.定义域:
2.值域:
3.恒过点 ,即x= 时,y=
4.在 R上是 函数
在R上是 函数
x
y
0
1
x
y
0
1
增
减
x>0,则ax>1
x<0,则ax<1
x>0,则ax<1
x<0,则ax>1
非奇非偶
例2.指数函数
的图象如下图所示,则底数
与正整数 1
共五个数,从小到大的顺序是 : .
x
y
0
1
1
指数函数的图像随底数大小的变化情况
例3 、比较下列各题中两个值的大小:
①
,
解① :利用指数函数单调性
,
的底数是1.7,它们可以看成函数
当 x=2.5和3时的函数值;
因为1.7>1,所以函数
在R上是增函数,
x
y
0
1
而2.5<3,所以,
2.5
3
y=1.7x
构造函数y=1.7x
利用单调性比较两个数的大小
②
.
③
④
.
.
例3 、比较下列各题中两个值的大小:
练习:判断大小
三.利用指数函数单调性比大小的方法 :
2. 中间量法(搭桥比较法):
用特殊的数1或0等.
1.构造函数的方法:(包括可转化为同底的)
关于过定点的问题
例4.函数 的图象过定点 .
关键点:a0=1(a≠0)
例5.解不等式
解:由指数函数的单调性可得:
整理得:
原不等式的解集为:
解得:
解简单的指数不等式
练习:1.解下列不等式
①
思考:解不等式(a>0且a≠1)
②
2.求定义域
例6.求定义域、值域:
解:(1)由x-1≠0得x≠1所以,所求函数定义域为
{x|x≠1}
⑴
⑵
由 ,得y≠1
所以,所求函数值域为{y|y>0且y≠1}
求函数的定义域、值域
说明:对于值域的求解,可以令
考察指数函数y=
并结合图象直观地得到:
函数值域为{y|y>0且y≠1}
⑵
解:
由5x-1≥0得
所以,所求函数定义域为
由
得y≥1
所以,所求函数值域为{y|y≥1}
练习:
1.求下列函数的定义域和值域:
⑴
(3)
复合函数的单调性
例8. 讨论函数 的单调性
练习.求函数 的单调区间
和值域.
x
-3
-2
-1
0
1
2
3
0.125
0.25
0.5
1
2
4
8
0.25
0.5
1
2
4
8
16
0.5
1
2
4
8
16
32
例:在同一坐标系下作出下列函数的图象,并指出
它们与指数函数y= 的图象的关系,
与
与
⑴
⑵
解:⑴列出函数数据表,作出图像
专题:图象的变换
比较函数y=
、y=
与y=
的关系:
的图象向左平行移动1个单位长度,
的图象;
的图象向左平行
移动2个单位长
度,就得到函数
y=
的图象。
将指数函数y=
就得到函数y=
将指数函数y=
1
x
o
y
y=2x+1
y=2x+2
y=2x
x
比较函数y=
、y=
与y=
的关系:
的图象向右平行移动1个单位长度,
的图象;
的图象向右平行移动2
个单位长度,就得到函
数y=
的图象。
将指数函数y=
就得到函数y=
将指数函数y=
y
y=2x-1
y=2x-2
y=2x
x
x
o
小结:将函数y=f(x)的图像向左(a>0)或向右(a<0)平移∣a∣个单位,即得函数y=f(x+a)的图像。
例. 已知函数
作出函数图象,求定义域、
与
图象的关系。
值域,并探讨
解:
定义域:R 值域:
作出图象如下:
练习: 已知函数
,作出图象,求定义域、值域。
函 数
y=f(x)
y=f(x+a)
y=f(x)+a
y=f(-x)
y=-f(x)
y=-f(-x)
y=f(|x|)
y=|f(x)|
对于有些复合函数的图象,常用基本函数图象+变换作出:即把我们熟知的基本函数图象,通过平移、作其对称图等方法,得到我们所要求作的复合函数的图象,这种方法我们遇到的主要有以下几种形式:
a>0时向左平移a个单位;a<0时向右平移|a|个单位.
a>0时向上平移a个单位;a<0时向下平移|a|个单位.
y=f(-x)与y=f(x)的图象关于y轴对称.
y=-f(x)与y=f(x)的图象关于x轴对称.
y=-f(-x)与y=f(x)的图象关于原点轴对称.
