北师大版高中数学必修1-3.3.3 指数函数的图像和性质 课件(17张PPT)
文档属性
| 名称 | 北师大版高中数学必修1-3.3.3 指数函数的图像和性质 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 606.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 06:47:43 | ||
图片预览





文档简介
3.3
指数函数的图像和性质
教学目标
知识与技能目标:归纳出并理解指数函数的图像和性质,培养学生实际应用函数的能力
方法目标:通过观察图像,分析、讨论、归纳指数函数的性质。体会数形结合的数学思想方法,培养学生发现、分析、解决问题的能力;
情感态度与价值观目标:在指数函数的学习过程中,体验数学的科学价值和应用价值,培养学生善于观察、勇于探索的良好习惯和严谨的科学态度。
重、难点
教学重点:指数函数图像和性质的归纳以及性质
的简单应用
教学难点: 用数形结合的方法从具体到一般
地探索指数函数的性质。
1、指数函数的定义:
一般地,函数
叫做指数函数,其中x是自变量,定义域是R
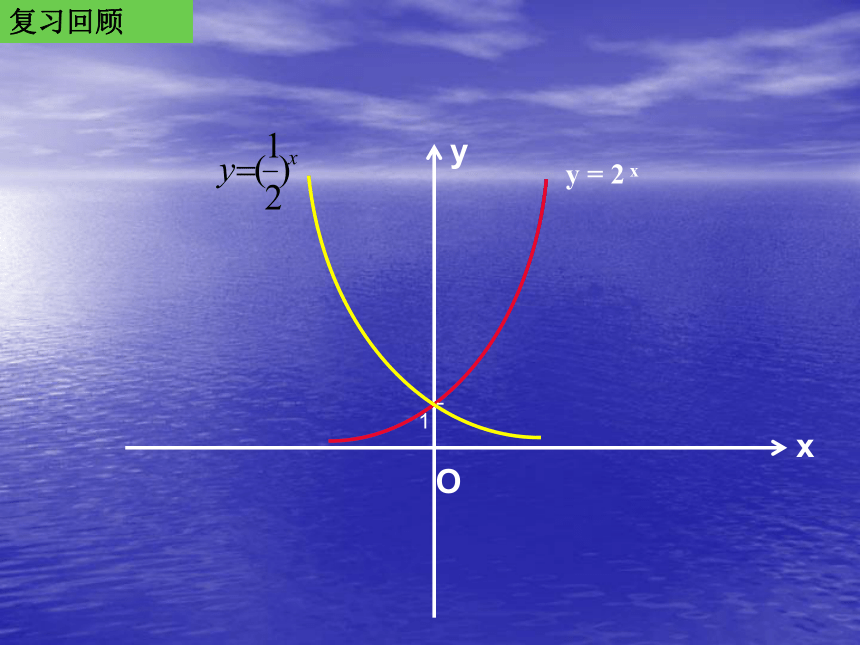
复习回顾
x
O
y
y = 2 x
复习回顾
1
函数
y=2x
y=(1/2)x
图
象
定点
R
定义域
性质
(0,1)即当x=0时,y=1
值域
在R上是增函数
在R上是减函数
若x>0, 则y
若x<0, 则
若x<0, 则
若x>0, 则
单调性
0y>1
>1
0那一般情况下指数函数
的图像与性质如何呢?下面我们通过几何画板
分别画出一些当a>1以及a>1时候的指数函数
图像
函数
y=ax (a>1)
y=ax (0图
象
定点
定义域
性质
值域
单调性
R
(0,1)即当x=0时,y=1
在R上是增函数
在R上是减函数
若x>0, 则y
若x<0, 则
若x<0, 则
若x>0, 则
0y>1
>1
0x
O
y
1
x
O
y
1
例1.比较下列各题中两个值的大小:
(1)1.52.5 ,1.5 3.2 ;
(2)0.5 – 1.2 ,0.5 – 1.5
(3)1.50.3 ,0.8 1.2
(1)1.52.5 ,1.5 3.2 ;
考察指数函数y=1.5x,
∵1.5>1
∴ y=1.5x是R上的增函数
又∵2.5<3.2
∴1.52.5< 1.53.2
解:
(2)0.5 – 1.2 ,0.5 – 1.5
考察指数函数y=0.5x,
∵0<0.5<1
∴ y=0.5x是R上的减函数
又∵-1.2>-1.5
∴ 0.5– 1.2 <0.5– 1.5
解:
(3)1.50.3 ,0.8 1.2
∵1.50.3>1.50=1,0.81.2<0.80=1
∴ 1.50.3>1,0.81.2<1
∴1.50.3>0.81.2
解:
(1)1.52.5 ,1.5 3.2 ;
(2)0.5 – 1.2 ,0.5 – 1.5
(3)1.50.3 ,0.8 1.2
例2 (1)解方程
变式2:解关于x的不等式:
变式1:解关于x的不等式:
原式可以化为:22x-1=22
∴ 2x-1=2
∴x=3/2
解:
当堂检测
1、比较下列各组数的大小
(1)2.3-2.3 2.3-3.3
(2)0.83.14 0.8π
(3)1.3-1.5 0.3-1.5
>
>
<
A.(-∞,1] B.[1,+ ∞)
C.(-∞,0] D. (-∞,0)
( )
C
已知a、b满足0<a<b<1,下列不等式成立的是( )
A.aa<ab B.aa<ba
C.bb<ab D.bb>ba
B
巩固提高
函数
y=ax (a>1)
y=ax (0图
象
定点
定义域
性质
值域
单调性
R
(0,1)即当x=0时,y=1
在R上是增函数
在R上是减函数
若x>0, 则y
若x<0, 则
若x<0, 则
若x>0, 则
0y>1
>1
0x
O
y
1
x
O
y
1
课堂小结
作业
必做题 P77:A组4,5
选做题 P77:B组2.
思考
已知
(1) 在同一坐标系中作出f(x)和g(x)的图像
(2)计算f(1)与g(-1),f(-π )与g(π ),f(m)与
g(-m)的值,从中你能得出什么结论?
指数函数的图像和性质
教学目标
知识与技能目标:归纳出并理解指数函数的图像和性质,培养学生实际应用函数的能力
方法目标:通过观察图像,分析、讨论、归纳指数函数的性质。体会数形结合的数学思想方法,培养学生发现、分析、解决问题的能力;
情感态度与价值观目标:在指数函数的学习过程中,体验数学的科学价值和应用价值,培养学生善于观察、勇于探索的良好习惯和严谨的科学态度。
重、难点
教学重点:指数函数图像和性质的归纳以及性质
的简单应用
教学难点: 用数形结合的方法从具体到一般
地探索指数函数的性质。
1、指数函数的定义:
一般地,函数
叫做指数函数,其中x是自变量,定义域是R
复习回顾
x
O
y
y = 2 x
复习回顾
1
函数
y=2x
y=(1/2)x
图
象
定点
R
定义域
性质
(0,1)即当x=0时,y=1
值域
在R上是增函数
在R上是减函数
若x>0, 则y
若x<0, 则
若x<0, 则
若x>0, 则
单调性
0
>1
0
的图像与性质如何呢?下面我们通过几何画板
分别画出一些当a>1以及a>1时候的指数函数
图像
函数
y=ax (a>1)
y=ax (0
象
定点
定义域
性质
值域
单调性
R
(0,1)即当x=0时,y=1
在R上是增函数
在R上是减函数
若x>0, 则y
若x<0, 则
若x<0, 则
若x>0, 则
0
>1
0
O
y
1
x
O
y
1
例1.比较下列各题中两个值的大小:
(1)1.52.5 ,1.5 3.2 ;
(2)0.5 – 1.2 ,0.5 – 1.5
(3)1.50.3 ,0.8 1.2
(1)1.52.5 ,1.5 3.2 ;
考察指数函数y=1.5x,
∵1.5>1
∴ y=1.5x是R上的增函数
又∵2.5<3.2
∴1.52.5< 1.53.2
解:
(2)0.5 – 1.2 ,0.5 – 1.5
考察指数函数y=0.5x,
∵0<0.5<1
∴ y=0.5x是R上的减函数
又∵-1.2>-1.5
∴ 0.5– 1.2 <0.5– 1.5
解:
(3)1.50.3 ,0.8 1.2
∵1.50.3>1.50=1,0.81.2<0.80=1
∴ 1.50.3>1,0.81.2<1
∴1.50.3>0.81.2
解:
(1)1.52.5 ,1.5 3.2 ;
(2)0.5 – 1.2 ,0.5 – 1.5
(3)1.50.3 ,0.8 1.2
例2 (1)解方程
变式2:解关于x的不等式:
变式1:解关于x的不等式:
原式可以化为:22x-1=22
∴ 2x-1=2
∴x=3/2
解:
当堂检测
1、比较下列各组数的大小
(1)2.3-2.3 2.3-3.3
(2)0.83.14 0.8π
(3)1.3-1.5 0.3-1.5
>
>
<
A.(-∞,1] B.[1,+ ∞)
C.(-∞,0] D. (-∞,0)
( )
C
已知a、b满足0<a<b<1,下列不等式成立的是( )
A.aa<ab B.aa<ba
C.bb<ab D.bb>ba
B
巩固提高
函数
y=ax (a>1)
y=ax (0
象
定点
定义域
性质
值域
单调性
R
(0,1)即当x=0时,y=1
在R上是增函数
在R上是减函数
若x>0, 则y
若x<0, 则
若x<0, 则
若x>0, 则
0
>1
0
O
y
1
x
O
y
1
课堂小结
作业
必做题 P77:A组4,5
选做题 P77:B组2.
思考
已知
(1) 在同一坐标系中作出f(x)和g(x)的图像
(2)计算f(1)与g(-1),f(-π )与g(π ),f(m)与
g(-m)的值,从中你能得出什么结论?
