北师大版高中数学必修1-3.3.3 指数函数及其性质 课件(28张PPT)
文档属性
| 名称 | 北师大版高中数学必修1-3.3.3 指数函数及其性质 课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 929.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 06:52:28 | ||
图片预览







文档简介
指数函数及其性质
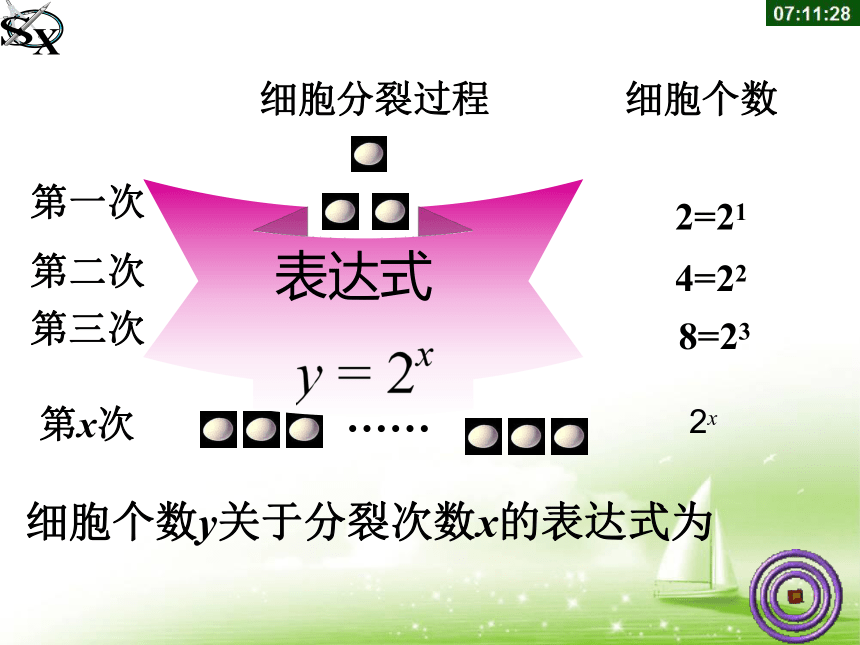
某种细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与分裂次数x的函数关系是什么?
实例分析
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达式为
表达式
2x
名句体验
天数
1
2
3
4
…
x
取出木棒
长度y
…
问题2: 庄子曰:一尺之棰,日取其半 ,万世不竭。求取出木棒的长度y与天数x的对应关系。
分析:把天数x与取出木棒长度y列出表格:
从解析式的角度,理解函数模型
底数是常数,自变量在指数位置.
能否用一个统一的式子表示上面函数?
y=ax
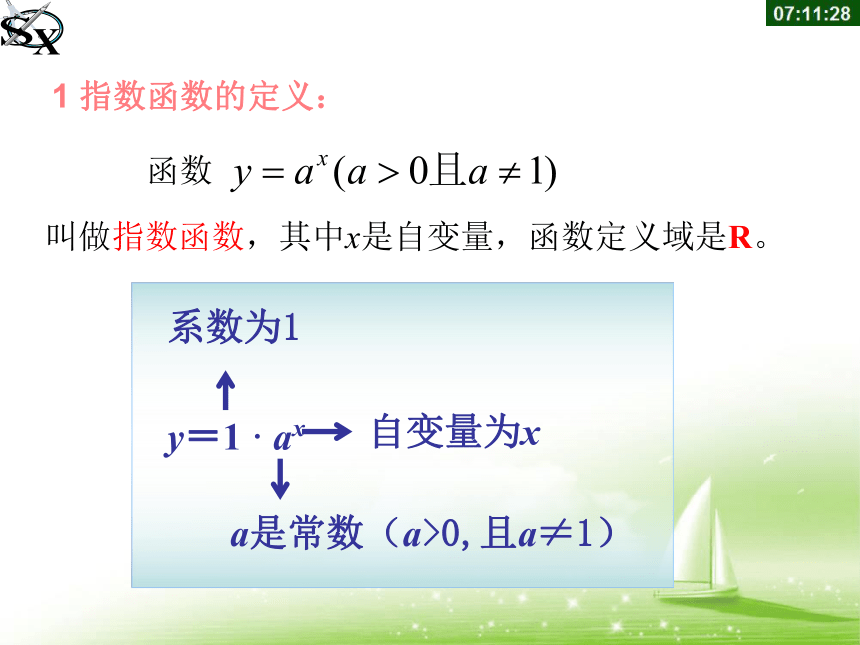
1 指数函数的定义:
函数
叫做指数函数,其中x是自变量,函数定义域是R。
自变量为x
系数为1
y=1 · ax
a是常数(a>0,且a≠1)
0时,
①若a=0,则当x>0时,
=0;
无意义.
当x
②若a<0,则对于x的某些数值,可使
无意义.
如
,这时对于x=
,x=
……等等,在实数范围内函数值不存在.
③若a=1,则对于任何x
R,
=1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且a?1。
?
?
0
1
a
指出下列函数哪些是指数函数
(1)(5)(6)(8)
概念辨析
例1已知指数函数
经过点(3,π),求
f(0)、f(1)、f(-3)的值.
的图像
2
我来演练
动手实践,合作交流
指数函数的图像是怎样的呢?
和
请同学们分两组分别画出下列函数的图像:
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
取值,列表
0
1
1
0
1
1
0
1
1
0
1
0
1
0
1
0
1
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
恒 过 点:
在 R 上是单调
在 R 上是单调
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
指数函数 的图像及性质
当 x> 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。
0
1
1
函数y=a x-1+4恒过定点( )
A.(1,5) B.(1,4) C.(0,4) D.(4,0)
理解新知
A
例2 比较下列各题中两个数的大小
底数相同
同底指数幂比大小,构造指数函数,利用函数单调性
不同底但可化同底
于是不等式的解集是
,
指数不等式利用指数函数的单调性进行求解
0
1
1
0
1
1
x
O
y
x=1
b
a
d
c
设a,b,c,d都是不等于1的正数,函数:
在同一直角坐标系中的图象如图所示.
则a,b,c,d的大小关系是
例4 比较下列各题中两个数的大小
利用中间量0,1 进行比较
底不同,指数也不同
正整数指数函数
一般地,如果函数y=ax(a>0,a≠1)的定义域是正整数集N+,则称它为正整数指数函数.
(1)正整数指数函数y=ax(a>0,a≠1,x∈N+)与指数函数y=ax(a>0, a≠1)单调性相同,函数图像不同
(2)指数函数的图像是曲线,正整数指数函数的图像是一群孤立的点
电冰箱使用的氟化物的释放会破坏大气层的臭氧层.臭氧含量Q近似满足关系式Q=Q00.9975t ,其中Q0是臭氧的初始量,t是时间(年).这里设Q0=1.
(1)计算经过20,40,60,80,100年后,臭氧含量Q;
(2)用图像表示每隔20年臭氧含量Q的变化;
(3)试分析随着时间的增加,臭氧含量Q是增加还是减少.
(3)通过计算和看图可知,随着时间的增加,臭氧的含量正在逐渐减少
(2)
学以致用
解(1)
课堂小结
1.通过本节课,你对指数函数有什么认识?
2.这节课主要通过什么方法来学习指数函数性质?
数形结合思想方法
从具体的到一般的学习方法
指数函数的定义
指数函数的图像和性质
1
x
o
y
y=1
1
2
-1
-2
2
3.记住两个基本图形
谢
!
谢
某种细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与分裂次数x的函数关系是什么?
实例分析
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达式为
表达式
2x
名句体验
天数
1
2
3
4
…
x
取出木棒
长度y
…
问题2: 庄子曰:一尺之棰,日取其半 ,万世不竭。求取出木棒的长度y与天数x的对应关系。
分析:把天数x与取出木棒长度y列出表格:
从解析式的角度,理解函数模型
底数是常数,自变量在指数位置.
能否用一个统一的式子表示上面函数?
y=ax
1 指数函数的定义:
函数
叫做指数函数,其中x是自变量,函数定义域是R。
自变量为x
系数为1
y=1 · ax
a是常数(a>0,且a≠1)
0时,
①若a=0,则当x>0时,
=0;
无意义.
当x
②若a<0,则对于x的某些数值,可使
无意义.
如
,这时对于x=
,x=
……等等,在实数范围内函数值不存在.
③若a=1,则对于任何x
R,
=1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且a?1。
?
?
0
1
a
指出下列函数哪些是指数函数
(1)(5)(6)(8)
概念辨析
例1已知指数函数
经过点(3,π),求
f(0)、f(1)、f(-3)的值.
的图像
2
我来演练
动手实践,合作交流
指数函数的图像是怎样的呢?
和
请同学们分两组分别画出下列函数的图像:
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
取值,列表
0
1
1
0
1
1
0
1
1
0
1
0
1
0
1
0
1
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
恒 过 点:
在 R 上是单调
在 R 上是单调
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
指数函数 的图像及性质
当 x> 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。
0
1
1
函数y=a x-1+4恒过定点( )
A.(1,5) B.(1,4) C.(0,4) D.(4,0)
理解新知
A
例2 比较下列各题中两个数的大小
底数相同
同底指数幂比大小,构造指数函数,利用函数单调性
不同底但可化同底
于是不等式的解集是
,
指数不等式利用指数函数的单调性进行求解
0
1
1
0
1
1
x
O
y
x=1
b
a
d
c
设a,b,c,d都是不等于1的正数,函数:
在同一直角坐标系中的图象如图所示.
则a,b,c,d的大小关系是
例4 比较下列各题中两个数的大小
利用中间量0,1 进行比较
底不同,指数也不同
正整数指数函数
一般地,如果函数y=ax(a>0,a≠1)的定义域是正整数集N+,则称它为正整数指数函数.
(1)正整数指数函数y=ax(a>0,a≠1,x∈N+)与指数函数y=ax(a>0, a≠1)单调性相同,函数图像不同
(2)指数函数的图像是曲线,正整数指数函数的图像是一群孤立的点
电冰箱使用的氟化物的释放会破坏大气层的臭氧层.臭氧含量Q近似满足关系式Q=Q00.9975t ,其中Q0是臭氧的初始量,t是时间(年).这里设Q0=1.
(1)计算经过20,40,60,80,100年后,臭氧含量Q;
(2)用图像表示每隔20年臭氧含量Q的变化;
(3)试分析随着时间的增加,臭氧含量Q是增加还是减少.
(3)通过计算和看图可知,随着时间的增加,臭氧的含量正在逐渐减少
(2)
学以致用
解(1)
课堂小结
1.通过本节课,你对指数函数有什么认识?
2.这节课主要通过什么方法来学习指数函数性质?
数形结合思想方法
从具体的到一般的学习方法
指数函数的定义
指数函数的图像和性质
1
x
o
y
y=1
1
2
-1
-2
2
3.记住两个基本图形
谢
!
谢
