30.1 二次函数同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
30.1二次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列y关于x的函数中,属于二次函数的是( )
A.y=x﹣1 B.y=
C.y=(x﹣1)2﹣x2 D.y=﹣2x2+1
2.若是二次函数,则a的值为( )
A. B.4 C. D.
3.已知二次函数y=ax2+4x+c,当x等于﹣2时,函数值是﹣1;当x=1时,函数值是5.则此二次函数的表达式为( )
A.y=2x2+4x﹣1 B.y=x2+4x﹣2
C.y=﹣2x2+4x+1 D.y=2x2+4x+1
4.下列函数中:①y=﹣ax2(a>0);②y=(a﹣1)x2(a<1);③y=﹣2x+a2(a≠0);④.具有过原点,且当x>0时,y随x增大而减小,这两个特征的有( )
A.1个 B.2个 C.3个 D.4个
5.对于函数y=x2,下列判断中,正确的是( )
A.若m、n互为相反数,则x=m与x=n对应的函数值相等
B.对于同一自变量x,有两个函数值与之对应
C.对于任意一个实数y,有两个x值与之对应
D.对于任何实数x,都有y>0
6.下列结论正确的是( )
A.y=ax2是二次函数 B.二次函数自变量的取值范围是所有实数
C.二次方程是二次函数的特例 D.二次函数的取值范围是非零实数
7.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售为x元,则可卖出(350-10x)件商品,那么商品所赚钱y元与售价x元的函数关系为( )
A. B.
C. D.
8.函数y=ax2+bx+c(a,b,c是常数)是二次函数的条件是( )
A.a≠0且b≠0 B.a≠0且b≠0,c≠0 C.a≠0 D.a,b,c为任意实数
二、填空题
9.已知函数y=(k+2)是关于x的二次函数,则k=________.
10.在二次函数中,二次项系数a=______,一次项系数b=______,常数项c=______.
11.已知二次函数的图象经过A(2,0),B(0,-6)两点.则这个二次函数的表达式为________________.
12.正方形边长为2,若边长增加x,那么面积增加y,则y与x的函数关系式是______.
三、解答题
13.当m为何值时,是二次函数?
14.已知抛物线交轴于A、B两点,点A在轴左侧,该图像对称轴为,最高点的纵坐标为4,且.
(1)求此二次函数的解析式;
(2)若点M在轴上方的抛物线上,且,求点M的坐标.
15.已知抛物线y=-x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为-1,∠PAO=45°,tan∠PBO=3/7.
(1)求P点的坐标;
(2)求抛物线的解析式.
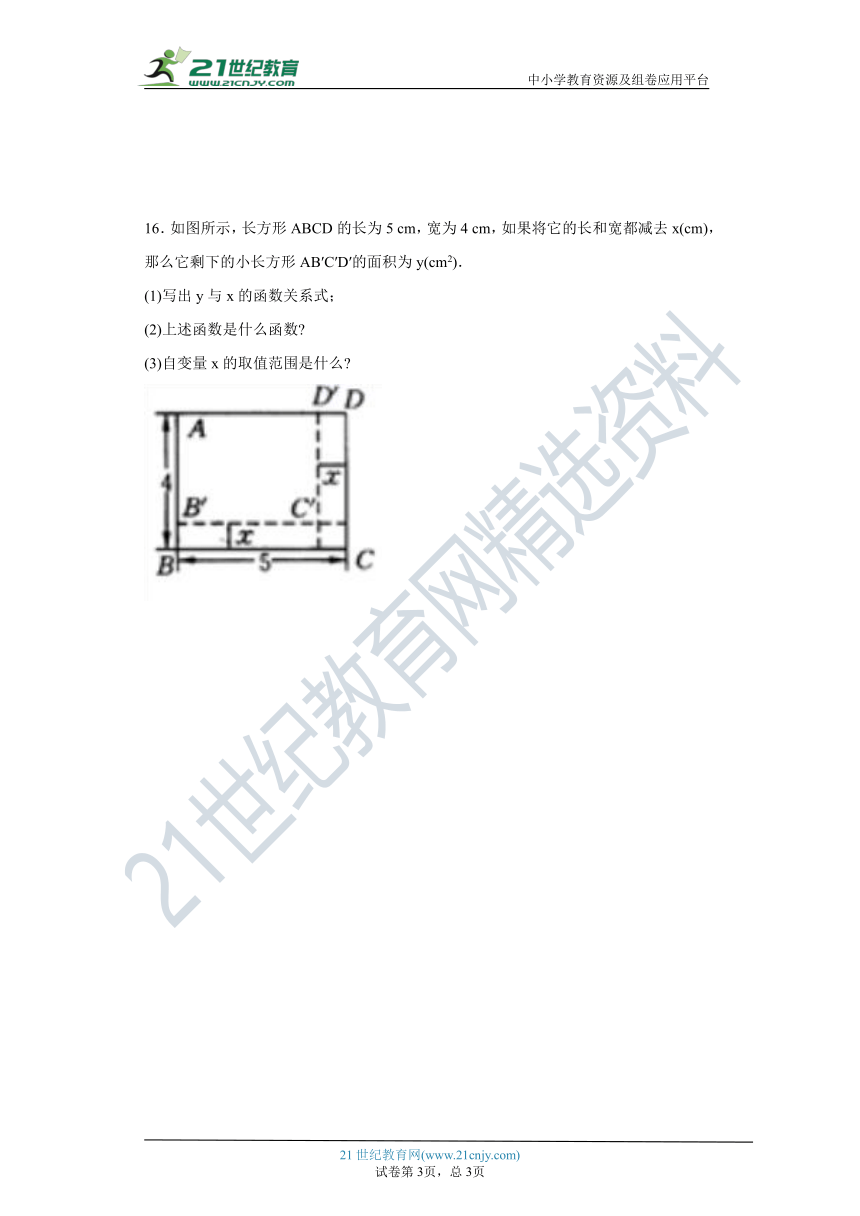
16.如图所示,长方形ABCD的长为5 cm,宽为4 cm,如果将它的长和宽都减去x(cm),那么它剩下的小长方形AB′C′D′的面积为y(cm2).
(1)写出y与x的函数关系式;
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
参考答案
1.D
解析:
解:A、该函数中自变量x的次数是1,属于一次函数,故本选项错误;
B、该函数是反比例函数,故本选项错误;
C、由已知函数关系式得到:y=﹣2x+1,属于一次函数,故本选项错误;
D、该函数符合二次函数定义,故本选项正确.
故选:D.
2.B
解析:
解:∵是二次函数,
∴
由①得:
由②得:
.
故选B.
3.A
解析:
解:根据题意得,解得,
所以抛物线解析式为y=2x2+4x﹣1.
故选A.
4.B
解析:
解:①∵y=﹣ax2(a>0)中a>0,
∴﹣a<0,
∴此函数图象过原点,且当x>0时,y随x增大而减小,故本小题正确;
②∵y=(a﹣1)x2(a<1),
∴a﹣1<0,
∴此函数图象过原点,且当x>0时,y随x增大而减小,故本小题正确;
③∵y=﹣2x+a2(a≠0)中,a≠0,
∴此函数的图象不过原点,故本小题错误;
④∵中a≠0,
∴此函数的图象不过原点,故本小题错误.
故选:B.
5.A
解析:
解:A.∵函数y=x2关于y轴对称,
∴若m、n互为相反数,则x=m与x=n对应的函数值相等正确,故本选项正确,
B.应为对于同一自变量x,有一个函数值与之对应,故本选项错误,
C、对于任意一个实数y,有两个x值与之对应错误,例如,x=0时,y有唯一的值0对应,故本选项错误;
D、x=0时,y=0,所以对于任何实数x,都有y>0错误,故本选项错误.
故选:A.
6.B
解析:
解:A、应强调a是常数,a≠0,错误;
B、二次函数解析式是整式,自变量可以取全体实数,正确;
C、二次方程不是二次函数,更不是二次函数的特例,错误;
D、二次函数的自变量取值有可能是零,如y=x2,当x=0时,y=0,错误.
故选:B.
7.D
解析:
解:每件的利润为(x-21),
∴y=(x-21)(350-10x)
=-10x2+560x-7350.
故选D.
8.C
解析:
由二次函数的定义得,函数y=ax2+bx+c(a,b,c是常数)是二次函数的条件是a≠0.
故选C.
9.2或-3
解析:
根据二次函数的定义列出方程与不等式解答即可.
∵函数y=(k+2)是关于x的二次函数,
∴k2+k﹣4=2,解得k=2或﹣3,
且k+2≠0,k≠﹣2.
故答案为: 2或﹣3.
10.3 -2 1
解析:
将变形得到,故可得二次项系数a=3,一次项系数b=-2,常数项c=1.
11.
解析:
把A(2,0)、B(0,-6)的坐标代入
解得:
所以二次函数的表达式为
12.y=x2+4x
解析:
新正方形的边长为,原正方形的边长为2.
新正方形的面积为,原正方形的面积为4,
,
故答案为.
13..
解析:
根据题意得,解得,故本题答案为4.
14.(1);(2)M(0,3)或(-2,3)
解析:
(1)由于抛物线有最高点,且与x轴有交点,
所以a<0;
∴A(?2,0),
∵图像对称轴为,最高点的纵坐标为4,
∴顶点坐标为(-1,4),
设抛物线的解析式为:y=a(x+1)2+4,
把A点坐标代入得a(-2+1)2+4=0,
解得a=-1;
故抛物线的解析式为:y=-x2-2x+3.
(2)由(1)的抛物线解析式可知:A(-3,0),B(1,0),
则AB=4;
由于S△ABM=AB?|yM|=6,
解得|yM|=3;
∵M点在x轴上方,
∴M点的纵坐标为3,代入抛物线的解析式中得:-x2-2x+3=3,
解得x=0,x=-2;
故M(0,3)或(-2,3).
15.(1) P为(-1,-3);(2)y=.
解析:
(1)如图,过P点作PD垂直x轴,垂足为D(分离出的图形见图2).
因为∠DAP=45°,所以PD=AD,
在Rt△PDBk ,DB=DA+AB=PD+4.
解之,得DP=3,
∴P点纵坐标为-3,故P为(-1,-3);
(2)OA=DA-OD=2,A(2,0),
又∵A、P两点在抛物线上,
∴解之,得,
∴y=.
16.(1) y=x2-9x+20;(2) 二次函数;(3) 0<x<4.
【解析】
试题分析:(1)根据长方形的面积公式,根据图示求解即可得到函数关系式;
(2)通过二次函数的定义可判断;
(3)根据x取值不能大于原方程的长方形的宽进行分析.
试题解析:(1)根据长方形的面积公式,得y=(5-x)·(4-x)=x2-9x+20,所以y与x的函数关系式为y=x2-9x+20.
(2)上述函数是二次函数.
(3)自变量x的取值范围是0<x<4.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
30.1二次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列y关于x的函数中,属于二次函数的是( )
A.y=x﹣1 B.y=
C.y=(x﹣1)2﹣x2 D.y=﹣2x2+1
2.若是二次函数,则a的值为( )
A. B.4 C. D.
3.已知二次函数y=ax2+4x+c,当x等于﹣2时,函数值是﹣1;当x=1时,函数值是5.则此二次函数的表达式为( )
A.y=2x2+4x﹣1 B.y=x2+4x﹣2
C.y=﹣2x2+4x+1 D.y=2x2+4x+1
4.下列函数中:①y=﹣ax2(a>0);②y=(a﹣1)x2(a<1);③y=﹣2x+a2(a≠0);④.具有过原点,且当x>0时,y随x增大而减小,这两个特征的有( )
A.1个 B.2个 C.3个 D.4个
5.对于函数y=x2,下列判断中,正确的是( )
A.若m、n互为相反数,则x=m与x=n对应的函数值相等
B.对于同一自变量x,有两个函数值与之对应
C.对于任意一个实数y,有两个x值与之对应
D.对于任何实数x,都有y>0
6.下列结论正确的是( )
A.y=ax2是二次函数 B.二次函数自变量的取值范围是所有实数
C.二次方程是二次函数的特例 D.二次函数的取值范围是非零实数
7.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售为x元,则可卖出(350-10x)件商品,那么商品所赚钱y元与售价x元的函数关系为( )
A. B.
C. D.
8.函数y=ax2+bx+c(a,b,c是常数)是二次函数的条件是( )
A.a≠0且b≠0 B.a≠0且b≠0,c≠0 C.a≠0 D.a,b,c为任意实数
二、填空题
9.已知函数y=(k+2)是关于x的二次函数,则k=________.
10.在二次函数中,二次项系数a=______,一次项系数b=______,常数项c=______.
11.已知二次函数的图象经过A(2,0),B(0,-6)两点.则这个二次函数的表达式为________________.
12.正方形边长为2,若边长增加x,那么面积增加y,则y与x的函数关系式是______.
三、解答题
13.当m为何值时,是二次函数?
14.已知抛物线交轴于A、B两点,点A在轴左侧,该图像对称轴为,最高点的纵坐标为4,且.
(1)求此二次函数的解析式;
(2)若点M在轴上方的抛物线上,且,求点M的坐标.
15.已知抛物线y=-x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为-1,∠PAO=45°,tan∠PBO=3/7.
(1)求P点的坐标;
(2)求抛物线的解析式.
16.如图所示,长方形ABCD的长为5 cm,宽为4 cm,如果将它的长和宽都减去x(cm),那么它剩下的小长方形AB′C′D′的面积为y(cm2).
(1)写出y与x的函数关系式;
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
参考答案
1.D
解析:
解:A、该函数中自变量x的次数是1,属于一次函数,故本选项错误;
B、该函数是反比例函数,故本选项错误;
C、由已知函数关系式得到:y=﹣2x+1,属于一次函数,故本选项错误;
D、该函数符合二次函数定义,故本选项正确.
故选:D.
2.B
解析:
解:∵是二次函数,
∴
由①得:
由②得:
.
故选B.
3.A
解析:
解:根据题意得,解得,
所以抛物线解析式为y=2x2+4x﹣1.
故选A.
4.B
解析:
解:①∵y=﹣ax2(a>0)中a>0,
∴﹣a<0,
∴此函数图象过原点,且当x>0时,y随x增大而减小,故本小题正确;
②∵y=(a﹣1)x2(a<1),
∴a﹣1<0,
∴此函数图象过原点,且当x>0时,y随x增大而减小,故本小题正确;
③∵y=﹣2x+a2(a≠0)中,a≠0,
∴此函数的图象不过原点,故本小题错误;
④∵中a≠0,
∴此函数的图象不过原点,故本小题错误.
故选:B.
5.A
解析:
解:A.∵函数y=x2关于y轴对称,
∴若m、n互为相反数,则x=m与x=n对应的函数值相等正确,故本选项正确,
B.应为对于同一自变量x,有一个函数值与之对应,故本选项错误,
C、对于任意一个实数y,有两个x值与之对应错误,例如,x=0时,y有唯一的值0对应,故本选项错误;
D、x=0时,y=0,所以对于任何实数x,都有y>0错误,故本选项错误.
故选:A.
6.B
解析:
解:A、应强调a是常数,a≠0,错误;
B、二次函数解析式是整式,自变量可以取全体实数,正确;
C、二次方程不是二次函数,更不是二次函数的特例,错误;
D、二次函数的自变量取值有可能是零,如y=x2,当x=0时,y=0,错误.
故选:B.
7.D
解析:
解:每件的利润为(x-21),
∴y=(x-21)(350-10x)
=-10x2+560x-7350.
故选D.
8.C
解析:
由二次函数的定义得,函数y=ax2+bx+c(a,b,c是常数)是二次函数的条件是a≠0.
故选C.
9.2或-3
解析:
根据二次函数的定义列出方程与不等式解答即可.
∵函数y=(k+2)是关于x的二次函数,
∴k2+k﹣4=2,解得k=2或﹣3,
且k+2≠0,k≠﹣2.
故答案为: 2或﹣3.
10.3 -2 1
解析:
将变形得到,故可得二次项系数a=3,一次项系数b=-2,常数项c=1.
11.
解析:
把A(2,0)、B(0,-6)的坐标代入
解得:
所以二次函数的表达式为
12.y=x2+4x
解析:
新正方形的边长为,原正方形的边长为2.
新正方形的面积为,原正方形的面积为4,
,
故答案为.
13..
解析:
根据题意得,解得,故本题答案为4.
14.(1);(2)M(0,3)或(-2,3)
解析:
(1)由于抛物线有最高点,且与x轴有交点,
所以a<0;
∴A(?2,0),
∵图像对称轴为,最高点的纵坐标为4,
∴顶点坐标为(-1,4),
设抛物线的解析式为:y=a(x+1)2+4,
把A点坐标代入得a(-2+1)2+4=0,
解得a=-1;
故抛物线的解析式为:y=-x2-2x+3.
(2)由(1)的抛物线解析式可知:A(-3,0),B(1,0),
则AB=4;
由于S△ABM=AB?|yM|=6,
解得|yM|=3;
∵M点在x轴上方,
∴M点的纵坐标为3,代入抛物线的解析式中得:-x2-2x+3=3,
解得x=0,x=-2;
故M(0,3)或(-2,3).
15.(1) P为(-1,-3);(2)y=.
解析:
(1)如图,过P点作PD垂直x轴,垂足为D(分离出的图形见图2).
因为∠DAP=45°,所以PD=AD,
在Rt△PDBk ,DB=DA+AB=PD+4.
解之,得DP=3,
∴P点纵坐标为-3,故P为(-1,-3);
(2)OA=DA-OD=2,A(2,0),
又∵A、P两点在抛物线上,
∴解之,得,
∴y=.
16.(1) y=x2-9x+20;(2) 二次函数;(3) 0<x<4.
【解析】
试题分析:(1)根据长方形的面积公式,根据图示求解即可得到函数关系式;
(2)通过二次函数的定义可判断;
(3)根据x取值不能大于原方程的长方形的宽进行分析.
试题解析:(1)根据长方形的面积公式,得y=(5-x)·(4-x)=x2-9x+20,所以y与x的函数关系式为y=x2-9x+20.
(2)上述函数是二次函数.
(3)自变量x的取值范围是0<x<4.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
