29.5 正多边形与圆同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
29.5正多边形与圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
2.正五边形的中心角等于( )
A.18° B.36° C.54° D.72°
3.以下说法正确的是
A.每个内角都是120°的六边形一定是正六边形.
B.正n边形的对称轴不一定有n条.
C.正n边形的每一个外角度数等于它的中心角度数.
D.正多边形一定既是轴对称图形,又是中心对称图形.
4.如图,⊙O是正方形ABCD的外接圆,点P在优弧上,则∠APB等于( )
A.30° B.45°
C.55° D.60°
5.如图所示,在中,,,.分别以,,为直径作半圆(以为直径的半圆恰好经过点,则图中阴影部分的面积是( )
A.4 B.5 C.7 D.6
6.如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线上的一点.若∠CBE=40°,则∠AOC等于( )
A.20° B.40° C.80° D.100°
7.圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是( ).
A.1:2:3:4 B.4:2:3:1 C.4:3:1:2 D.4:1:3:2
二、填空题
8.如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为_____.
9.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC=____°.
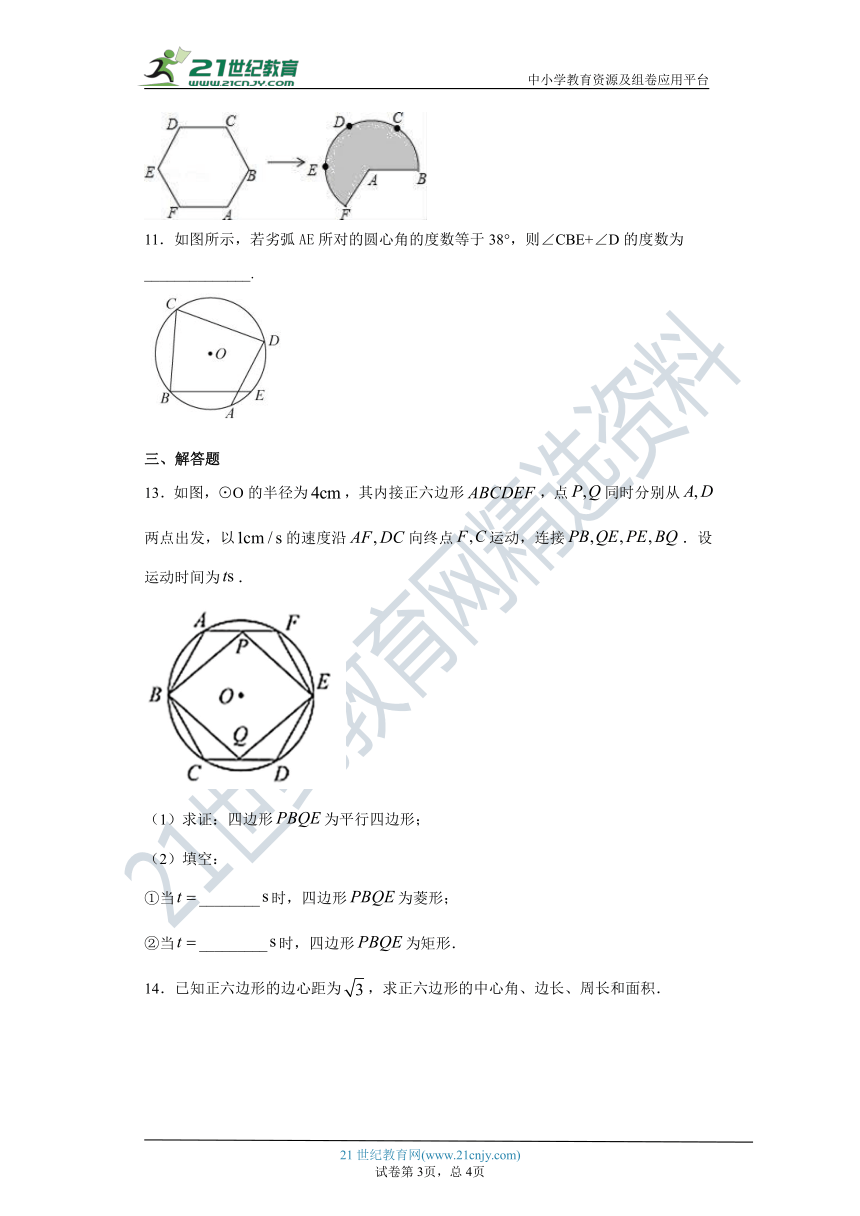
10.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为_____.
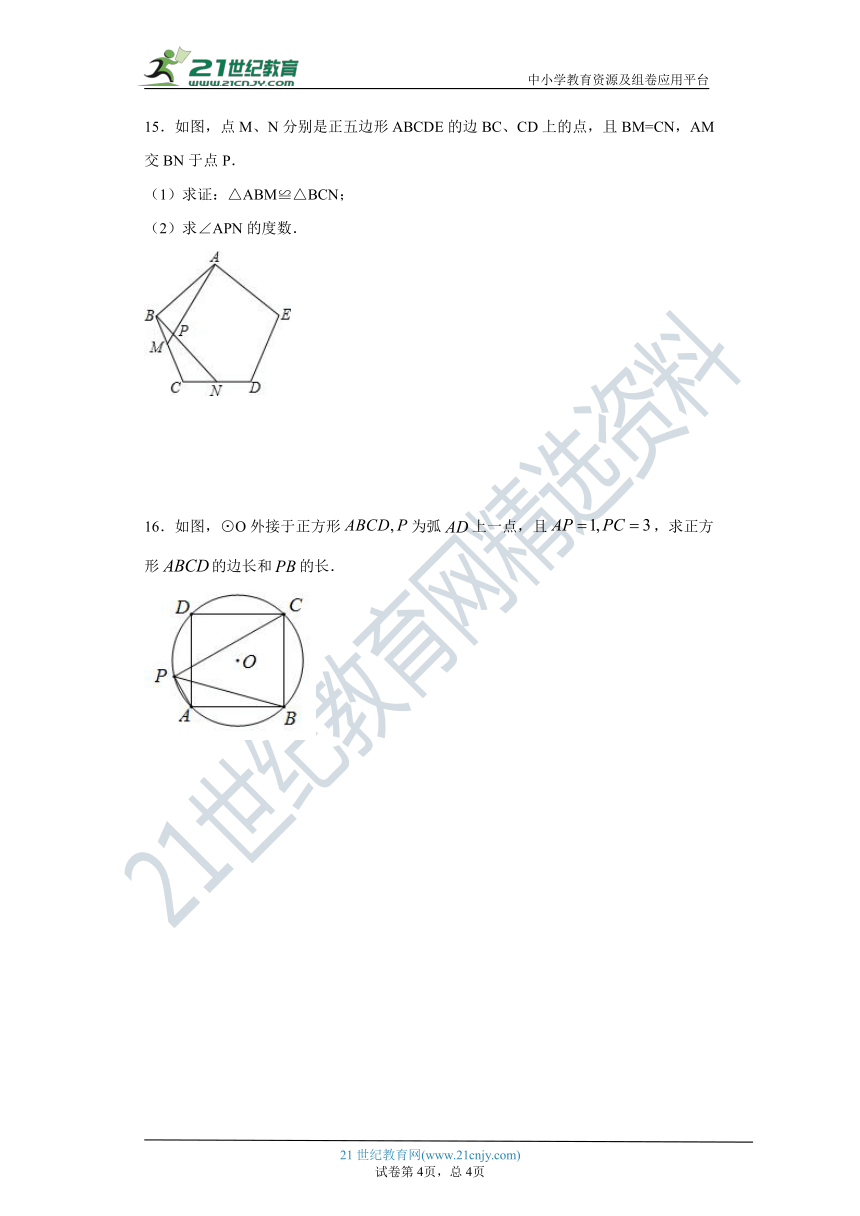
11.如图所示,若劣弧AE所对的圆心角的度数等于38°,则∠CBE+∠D的度数为______________.
三、解答题
13.如图,⊙O的半径为,其内接正六边形,点同时分别从两点出发,以的速度沿向终点运动,连接.设运动时间为.
(1)求证:四边形为平行四边形;
(2)填空:
①当________时,四边形为菱形;
②当_________时,四边形为矩形.
已知正六边形的边心距为,求正六边形的中心角、边长、周长和面积.
15.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
16.如图,⊙O外接于正方形为弧上一点,且,求正方形的边长和的长.
参考答案
1.B
解析:
解:∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,
而∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
而∠BAD=105°,
∴∠DCE=105°.
故选B.
2.D
解析:
解:正五边形的中心角为.
故选D
3.C
解析:
解:A选项不正确;因为每个角都是120°?的六边形可以是空间六边形;
B选项不正确;正n边形的对称轴一定由n条;
C选项正确;因为正n边形的每一个外角度数等于它的中心角度数;
D选项不正确;因为当正n边形的边数为偶数时才既是轴对称图形又是中心对称图形;
故选:C.
4.B
解析:
连接OA、OB,
∵⊙O是正方形ABCD的外接圆,
∴∠AOB=90°,
∴∠APB==∠AOB=45°,
故选B.
5.D
解析:
解:在中
∵,,
∴,
∴BC=3,
∴阴影部分的面积=以AB为直径的半圆面积+以BC为直径的半圆面积+-以AC为直径的半圆面积=6.故选D.
6.C
解析:
因为四边形ABCD为⊙O的内接四边形,∠CBE=40°,所以∠D=40°,所以∠AOC=80°.
7.C
解析:
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=∠B+∠D=180°.
∴圆内接四边形ABCD的四个内角之比可能是:4:3:1:2.
故选C.
8.C
解析:
∵扇形的圆心角是360°×40%=144°,∴弧长l=
设底面半径是r,则有=2πr,则r=2,
圆锥的高h=.
故选C.
9.72°
解析:
∵五边形ABCDE为正五边形,
∴AB=BC=AE,∠ABC=∠BAE=108°,
∴∠BAC=∠BCA=∠ABE=∠AEB=(180°?108°)÷2=36°,
∴∠AFE=∠BAC+∠ABE=72°,
故答案为72°.
10.115°
解析:
解:连接OC,如右图所示,
由题意可得,∠OCP=90°,∠P=40°,
∴∠COB=50°,
∵OC=OB,
∴∠OCB=∠OBC=65°,
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=115°,
故答案为:115°.
11.18
解析:
解:∵正六边形ABCDEF的边长为3,
∴AB=BC=CD=DE=EF=FA=3,
∴弧BAF的长=3×6﹣3﹣3═12,
∴扇形AFB(阴影部分)的面积=×12×3=18.
故答案为18.
12.161°.
解析:
连接BA,则∠ABE=×38°=19°.因カ四边形ABCD是圆内接四边形,所以∠ABC+∠D=180°,所以∠CBE+∠D=180°-19°=161°.
13.(1)见解析;(2)①2;②0或4
解析:
(1)∵正六边形内接于的半径为4,
,
∵点同时分别从两点出发,以的速度沿向终点运动,.
在和中,
同理可证.
∴四边形是平行四边形.
(2)①2;②0或4 ,
①由对称性可知,当,时,四边形是菱形,此时.
②当时,点在点处, ,,此时四边形是矩形.
当时,点在点处,同理可得,此时四边形是矩形.综上所述,当或时,四边形是矩形.
14.六边形的中心角为60°,边长为2,周长为12,面积为6.
解析:
试题分析:首先根据题意作出图形,然后可得△OBC是等边三角形,然后由三角函数的性质,求得OB的长,继而求得正六边形的中心角、边长、周长和面积.
试题解析:如图,连接OB、OC,过点O作OH⊥BC于点H,
∵六边形ABCDEF是正六边形,∴∠BOC=×360°=60°.
∵OB=OC,∴△OBC是等边三角形.
∴∠OBC=60°,BC=OB=OC.
∵OH=,sin∠OBC=,
∴OB=BC=2.
∴正六边形的周长为2×6=12.
∴S正六边形ABCDEF=6S△OBC=6× ×2× =6 .
∴正六边形的中心角为60°,边长为2,周长为12,面积为6.
15.解析:
(1)∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
,
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°.
即∠APN的度数为108°.
16.,
解析:
解:连接,作于点,
如图所示.
∵四边形是正方形,
,
是的直径,是等腰直角三角形,
是等腰直角三角形,
,
.
正方形的边长为的长为.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
29.5正多边形与圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
2.正五边形的中心角等于( )
A.18° B.36° C.54° D.72°
3.以下说法正确的是
A.每个内角都是120°的六边形一定是正六边形.
B.正n边形的对称轴不一定有n条.
C.正n边形的每一个外角度数等于它的中心角度数.
D.正多边形一定既是轴对称图形,又是中心对称图形.
4.如图,⊙O是正方形ABCD的外接圆,点P在优弧上,则∠APB等于( )
A.30° B.45°
C.55° D.60°
5.如图所示,在中,,,.分别以,,为直径作半圆(以为直径的半圆恰好经过点,则图中阴影部分的面积是( )
A.4 B.5 C.7 D.6
6.如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线上的一点.若∠CBE=40°,则∠AOC等于( )
A.20° B.40° C.80° D.100°
7.圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是( ).
A.1:2:3:4 B.4:2:3:1 C.4:3:1:2 D.4:1:3:2
二、填空题
8.如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为_____.
9.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC=____°.
10.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为_____.
11.如图所示,若劣弧AE所对的圆心角的度数等于38°,则∠CBE+∠D的度数为______________.
三、解答题
13.如图,⊙O的半径为,其内接正六边形,点同时分别从两点出发,以的速度沿向终点运动,连接.设运动时间为.
(1)求证:四边形为平行四边形;
(2)填空:
①当________时,四边形为菱形;
②当_________时,四边形为矩形.
已知正六边形的边心距为,求正六边形的中心角、边长、周长和面积.
15.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
16.如图,⊙O外接于正方形为弧上一点,且,求正方形的边长和的长.
参考答案
1.B
解析:
解:∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,
而∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
而∠BAD=105°,
∴∠DCE=105°.
故选B.
2.D
解析:
解:正五边形的中心角为.
故选D
3.C
解析:
解:A选项不正确;因为每个角都是120°?的六边形可以是空间六边形;
B选项不正确;正n边形的对称轴一定由n条;
C选项正确;因为正n边形的每一个外角度数等于它的中心角度数;
D选项不正确;因为当正n边形的边数为偶数时才既是轴对称图形又是中心对称图形;
故选:C.
4.B
解析:
连接OA、OB,
∵⊙O是正方形ABCD的外接圆,
∴∠AOB=90°,
∴∠APB==∠AOB=45°,
故选B.
5.D
解析:
解:在中
∵,,
∴,
∴BC=3,
∴阴影部分的面积=以AB为直径的半圆面积+以BC为直径的半圆面积+-以AC为直径的半圆面积=6.故选D.
6.C
解析:
因为四边形ABCD为⊙O的内接四边形,∠CBE=40°,所以∠D=40°,所以∠AOC=80°.
7.C
解析:
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=∠B+∠D=180°.
∴圆内接四边形ABCD的四个内角之比可能是:4:3:1:2.
故选C.
8.C
解析:
∵扇形的圆心角是360°×40%=144°,∴弧长l=
设底面半径是r,则有=2πr,则r=2,
圆锥的高h=.
故选C.
9.72°
解析:
∵五边形ABCDE为正五边形,
∴AB=BC=AE,∠ABC=∠BAE=108°,
∴∠BAC=∠BCA=∠ABE=∠AEB=(180°?108°)÷2=36°,
∴∠AFE=∠BAC+∠ABE=72°,
故答案为72°.
10.115°
解析:
解:连接OC,如右图所示,
由题意可得,∠OCP=90°,∠P=40°,
∴∠COB=50°,
∵OC=OB,
∴∠OCB=∠OBC=65°,
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=115°,
故答案为:115°.
11.18
解析:
解:∵正六边形ABCDEF的边长为3,
∴AB=BC=CD=DE=EF=FA=3,
∴弧BAF的长=3×6﹣3﹣3═12,
∴扇形AFB(阴影部分)的面积=×12×3=18.
故答案为18.
12.161°.
解析:
连接BA,则∠ABE=×38°=19°.因カ四边形ABCD是圆内接四边形,所以∠ABC+∠D=180°,所以∠CBE+∠D=180°-19°=161°.
13.(1)见解析;(2)①2;②0或4
解析:
(1)∵正六边形内接于的半径为4,
,
∵点同时分别从两点出发,以的速度沿向终点运动,.
在和中,
同理可证.
∴四边形是平行四边形.
(2)①2;②0或4 ,
①由对称性可知,当,时,四边形是菱形,此时.
②当时,点在点处, ,,此时四边形是矩形.
当时,点在点处,同理可得,此时四边形是矩形.综上所述,当或时,四边形是矩形.
14.六边形的中心角为60°,边长为2,周长为12,面积为6.
解析:
试题分析:首先根据题意作出图形,然后可得△OBC是等边三角形,然后由三角函数的性质,求得OB的长,继而求得正六边形的中心角、边长、周长和面积.
试题解析:如图,连接OB、OC,过点O作OH⊥BC于点H,
∵六边形ABCDEF是正六边形,∴∠BOC=×360°=60°.
∵OB=OC,∴△OBC是等边三角形.
∴∠OBC=60°,BC=OB=OC.
∵OH=,sin∠OBC=,
∴OB=BC=2.
∴正六边形的周长为2×6=12.
∴S正六边形ABCDEF=6S△OBC=6× ×2× =6 .
∴正六边形的中心角为60°,边长为2,周长为12,面积为6.
15.解析:
(1)∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
,
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°.
即∠APN的度数为108°.
16.,
解析:
解:连接,作于点,
如图所示.
∵四边形是正方形,
,
是的直径,是等腰直角三角形,
是等腰直角三角形,
,
.
正方形的边长为的长为.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
