29.4 切线长定理同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
29.4切线长定理*
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知圆O的半径为R,点O到直线m的距离为d、R、d是方程x2﹣4x+a=0的两根,当直线m与圆O相切时,a的值是( )
A.3 B.4 C.5 D.无法确定
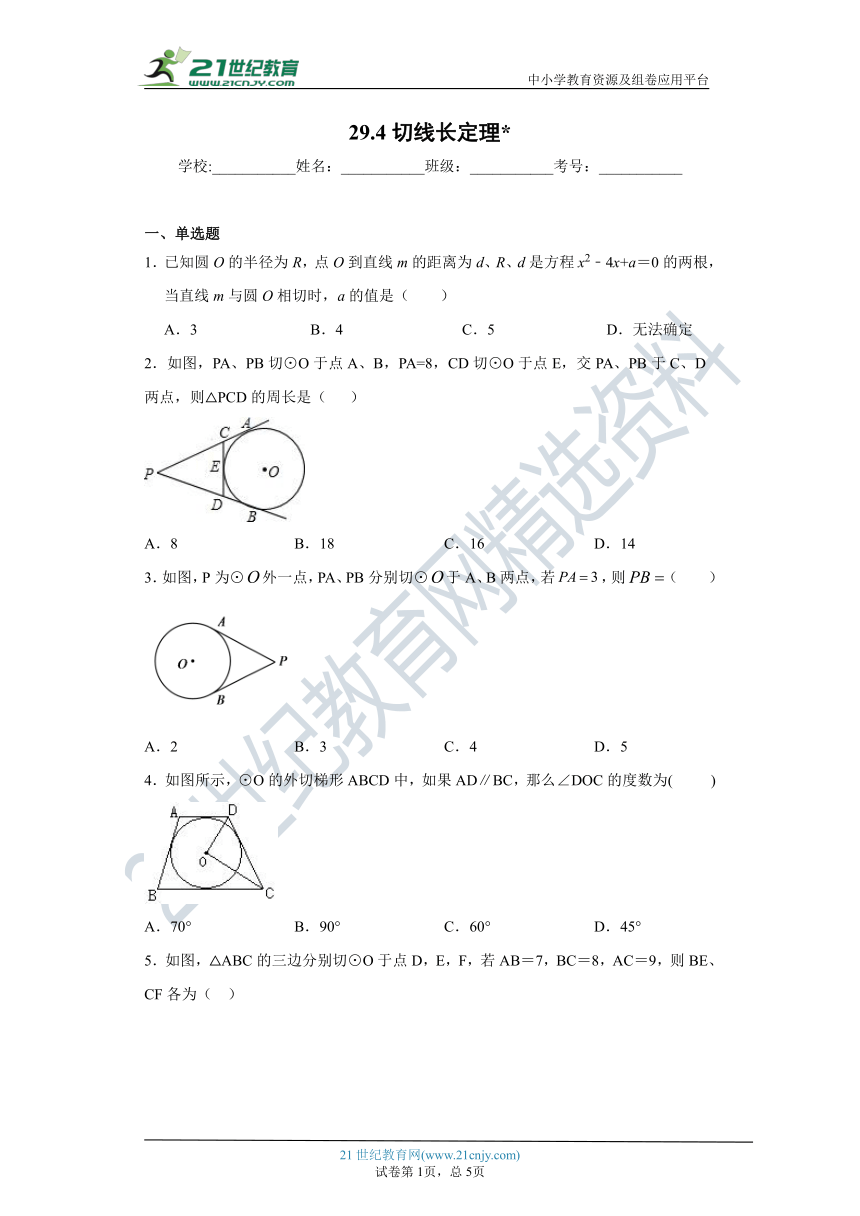
2.如图,PA、PB切⊙O于点A、B,PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( )
A.8 B.18 C.16 D.14
3.如图,P为⊙外一点,PA、PB分别切⊙于A、B两点,若,则( )
A.2 B.3 C.4 D.5
4.如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( )
A.70° B.90° C.60° D.45°
5.如图,△ABC的三边分别切⊙O于点D,E,F,若AB=7,BC=8,AC=9,则BE、CF各为( )
A.2, 4 B.2,5 C.1, 4 D.3, 5
6.圆外切等腰梯形的中位线等于8,则一腰长等于( )
A.4 B.6 C.8 D.10
7.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为( )
A.130° B.120° C.110° D.100°
8.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )
A.5,(90°+∠P) B.7,90°+
C.10,90°-∠P D.10,90°+∠P
二、填空题
9.如图,PA 、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上,若PA长为2,则△PEF的周长是_____.
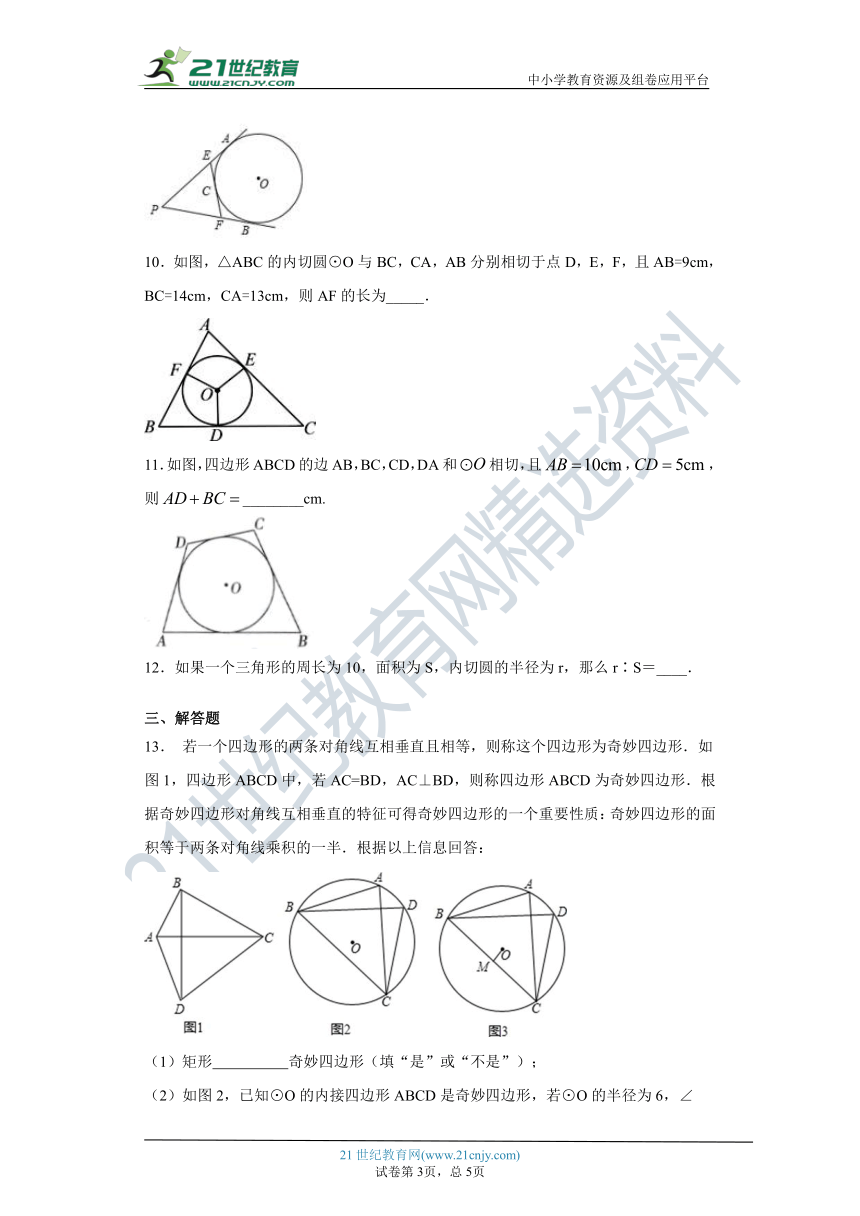
10.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,则AF的长为_____.
11.如图,四边形ABCD的边AB,BC,CD,DA和相切,且,,则________cm.
12.如果一个三角形的周长为10,面积为S,内切圆的半径为r,那么r∶S=____.
三、解答题
13. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)矩形 奇妙四边形(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为6,∠ BCD=60°.求奇妙四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是奇妙四边形作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
14.如图,AB是⊙O直径,⊙O过AC的中点D,DE⊥BC,垂足为E.
(1)由这些条件,你能得出哪些结论?(要求:不准标其他字母,找结论过程中所连的辅助线不能出现在结论中,不写推理过程,写出4个结论即可)
(2)若∠ABC为直角,其他条件不变,除上述结论外你还能推出哪些新的正确结论?并画出图形.(要求:写出6个结论即可,其他要求同(1))
15.如图,是的直径,过外一点作的两条切线,,切点分别为,,连接,.
(1)求证:;
(2)连接,,若,,,求的长.
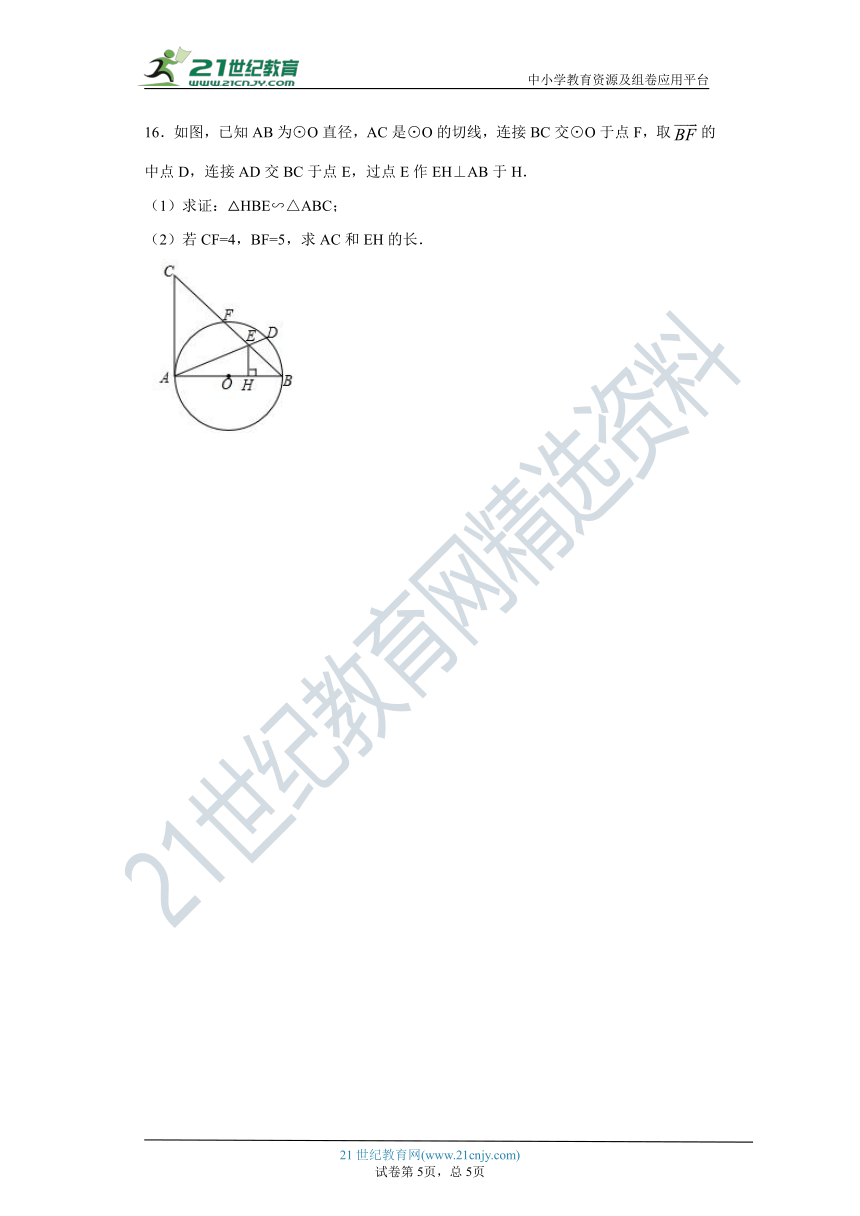
16.如图,已知AB为⊙O直径,AC是⊙O的切线,连接BC交⊙O于点F,取的中点D,连接AD交BC于点E,过点E作EH⊥AB于H.
(1)求证:△HBE∽△ABC;
(2)若CF=4,BF=5,求AC和EH的长.
参考答案
解析:
解:∵直线和圆相切,
∴d=R,
∴△=16﹣4a=0,
∴a=4,
故选:B.
2.C
解析:
解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,
∴PB=PA=8,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD=PC+CE+DE+PC=PC+CA+DB+PD=PA+PB=16.
故选C.
3.B
解析:
因为PA和PB与⊙相切,根据切线长定理,所以PA=PB=3,故选B.
4.B
解析:
∵DA、CD、CB都与⊙O相切,
∴∠ADO=∠ODC,∠OCD=∠OCB;
∵AD∥BC,
∴∠ADC+∠BCD=180°;
∴∠ODC+∠OCD=90°,即∠DOC=90°;
故选B.
5.D
解析:
设BE=x,则CE=BC?BE=8?x,
∵△ABC的三边分别切⊙O于点D,E,F,
∴BD=BE=x,CF=CE=8?x,AD=AF,
∴AD=AB?BD=7?x,
∴AF=7?x,
∵AF+FC=AC=9,
∴7?x+8?x=9,
∴x=3,
∴CF=8?3=5.
故答案为D.
6.C
解析:
如图:
设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,
∴MN=(AB+CD),
根据切线长定理得:
DE=DH,CF=CH,并且等腰梯形和圆都是轴对称图形,
∴CD=DH+CH=DE+CF=(AB+CD),
∴CD=MN,而MN=8,
∴CD=8.
故选C.
7.C
解析:
∵AB、AC是⊙O的两条切线,B、C是切点,
∴∠B=∠C=90°,∠BOC=180°-∠A=110°.
故选C.
8.C
解析:
∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=10,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA=10,
如图,连接OA、OE、OB.
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=∠AOB,
∴∠AOB=180°-∠P,
∴∠COD=90°-∠P.
故选C.
9.4.
解析:
考点:切线的性质.
分析:由切线长定理知,AE=CE,FB=CF,PA=PB=2,然后根据△PEF的周长公式即可求出其结果.
解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在上,
∴AE=CE,FB=CF,PA=PB=2,
∴△PEF的周长=PE+EF+PF=PA+PB=4.
故填空答案:4.
10.4 cm
解析:
设AF=acm,
∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,
∴AF=AE,CE=CD,BF=BD,
∵AB=9cm,BC=14cm,CA=13cm,
∴BD=BF=(9-a)cm,CD=CE=(13-a)cm,
∵BD+CD=BC=14cm,
∴(9-a)+(13-a)=14,
解得:a=4,
即AF=4cm.
故答案为4cm.
11.15.
解析:
∵四边形ABCD的边AB、BC、CD、DA和O分别切于L、M、N、P,
∴AP=AL,BM=BL,CM=CN,DN=DP,
∴AL+BL+DN+CN=AP+BM+DP+CM,
即AB+CD=AD+BC,
∵AB=10cm,CD=5cm,
∴AB+CD =15cm,故答案为15.
12.1∶5
解析:
由题意得:S=??l?×r,即S=???×10×r,∴r:s=1:5
故答案为:1:5.
13.(1)不是;
(2)54;
(3).
解析:
解:(1)矩形的对角线相等但不垂直,
所以矩形不是奇妙四边形;
故答案为不是;
(2)
连结OB、OD,作OH⊥BD于H,如图2,则BH=DH,
∵∠BOD=2∠BCD=2×60°=120°,
∴在等腰△OBD中,∠OBD=30°,
在Rt△OBH中,∵∠OBH=30°,
∴,
∴
∴
∵四边形ABCD是奇妙四边形,
∴,
∴;
(3).
理由如下:
连结OB、OC、OA、OD,作OE⊥AD于E,如图3,
∵OE⊥AD,
∴在等腰△AOD中,,
又∵,
∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,
∴∠BAC+∠ABD=90°,
∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,
∴∠OBM=∠AOE,
在△BOM和△OAE中
∴,
∴OM=AE,
∴.
14.见解析
解析:
①DE与⊙O相切,AB=BC,DE2+CE2=CD2,∠C+∠CDE=90°
BC是⊙O的切线,有2DE=2AB等.
15.(1)证明见解析;(2).
解析:
(1)证明:∵、与相切于、.
∴,平分.
在等腰中,,平分.
∴于,即.
(2)解:连接、.
∵
∴
∴
同理:
∴.
在等腰中,.
∴.
∵与相切于.
∴.
∴.
在中,,
∴.
16.(1)证明见解析;(2)CA=6,EH=2.
解析:
分析:(1)根据切线的性质即可证明:∠CAB=∠EHB,由此即可解决问题;
(2)连接AF.由△CAF∽△CBA,推出CA2=CF?CB=36,推出CA=6,AB=,AF=,由Rt△AEF≌Rt△AEH,推出AF=AH=2,设EF=EH=x.在Rt△EHB中,可得(5﹣x)2=x2+()2,解方程即可解决问题;
详解:(1)∵AC是⊙O的切线,
∴CA⊥AB.
∵EH⊥AB,
∴∠EHB=∠CAB.
∵∠EBH=∠CBA,
∴△HBE∽△ABC.
(2)连接AF.
∵AB是直径,
∴∠AFB=90°.
∵∠C=∠C,∠CAB=∠AFC,
∴△CAF∽△CBA,
∴CA2=CF?CB=36,
∴CA=6,AB=,AF=.
∵,
∴∠EAF=∠EAH.
∵EF⊥AF,EH⊥AB,
∴EF=EH.
∵AE=AE,
∴Rt△AEF≌Rt△AEH,
∴AF=AH=2.
设EF=EH=x.在Rt△EHB中,(5﹣x)2=x2+()2,
∴x=2,
∴EH=2.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
29.4切线长定理*
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知圆O的半径为R,点O到直线m的距离为d、R、d是方程x2﹣4x+a=0的两根,当直线m与圆O相切时,a的值是( )
A.3 B.4 C.5 D.无法确定
2.如图,PA、PB切⊙O于点A、B,PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( )
A.8 B.18 C.16 D.14
3.如图,P为⊙外一点,PA、PB分别切⊙于A、B两点,若,则( )
A.2 B.3 C.4 D.5
4.如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( )
A.70° B.90° C.60° D.45°
5.如图,△ABC的三边分别切⊙O于点D,E,F,若AB=7,BC=8,AC=9,则BE、CF各为( )
A.2, 4 B.2,5 C.1, 4 D.3, 5
6.圆外切等腰梯形的中位线等于8,则一腰长等于( )
A.4 B.6 C.8 D.10
7.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为( )
A.130° B.120° C.110° D.100°
8.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )
A.5,(90°+∠P) B.7,90°+
C.10,90°-∠P D.10,90°+∠P
二、填空题
9.如图,PA 、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上,若PA长为2,则△PEF的周长是_____.
10.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,则AF的长为_____.
11.如图,四边形ABCD的边AB,BC,CD,DA和相切,且,,则________cm.
12.如果一个三角形的周长为10,面积为S,内切圆的半径为r,那么r∶S=____.
三、解答题
13. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)矩形 奇妙四边形(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为6,∠ BCD=60°.求奇妙四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是奇妙四边形作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
14.如图,AB是⊙O直径,⊙O过AC的中点D,DE⊥BC,垂足为E.
(1)由这些条件,你能得出哪些结论?(要求:不准标其他字母,找结论过程中所连的辅助线不能出现在结论中,不写推理过程,写出4个结论即可)
(2)若∠ABC为直角,其他条件不变,除上述结论外你还能推出哪些新的正确结论?并画出图形.(要求:写出6个结论即可,其他要求同(1))
15.如图,是的直径,过外一点作的两条切线,,切点分别为,,连接,.
(1)求证:;
(2)连接,,若,,,求的长.
16.如图,已知AB为⊙O直径,AC是⊙O的切线,连接BC交⊙O于点F,取的中点D,连接AD交BC于点E,过点E作EH⊥AB于H.
(1)求证:△HBE∽△ABC;
(2)若CF=4,BF=5,求AC和EH的长.
参考答案
解析:
解:∵直线和圆相切,
∴d=R,
∴△=16﹣4a=0,
∴a=4,
故选:B.
2.C
解析:
解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,
∴PB=PA=8,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD=PC+CE+DE+PC=PC+CA+DB+PD=PA+PB=16.
故选C.
3.B
解析:
因为PA和PB与⊙相切,根据切线长定理,所以PA=PB=3,故选B.
4.B
解析:
∵DA、CD、CB都与⊙O相切,
∴∠ADO=∠ODC,∠OCD=∠OCB;
∵AD∥BC,
∴∠ADC+∠BCD=180°;
∴∠ODC+∠OCD=90°,即∠DOC=90°;
故选B.
5.D
解析:
设BE=x,则CE=BC?BE=8?x,
∵△ABC的三边分别切⊙O于点D,E,F,
∴BD=BE=x,CF=CE=8?x,AD=AF,
∴AD=AB?BD=7?x,
∴AF=7?x,
∵AF+FC=AC=9,
∴7?x+8?x=9,
∴x=3,
∴CF=8?3=5.
故答案为D.
6.C
解析:
如图:
设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,
∴MN=(AB+CD),
根据切线长定理得:
DE=DH,CF=CH,并且等腰梯形和圆都是轴对称图形,
∴CD=DH+CH=DE+CF=(AB+CD),
∴CD=MN,而MN=8,
∴CD=8.
故选C.
7.C
解析:
∵AB、AC是⊙O的两条切线,B、C是切点,
∴∠B=∠C=90°,∠BOC=180°-∠A=110°.
故选C.
8.C
解析:
∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=10,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA=10,
如图,连接OA、OE、OB.
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=∠AOB,
∴∠AOB=180°-∠P,
∴∠COD=90°-∠P.
故选C.
9.4.
解析:
考点:切线的性质.
分析:由切线长定理知,AE=CE,FB=CF,PA=PB=2,然后根据△PEF的周长公式即可求出其结果.
解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在上,
∴AE=CE,FB=CF,PA=PB=2,
∴△PEF的周长=PE+EF+PF=PA+PB=4.
故填空答案:4.
10.4 cm
解析:
设AF=acm,
∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,
∴AF=AE,CE=CD,BF=BD,
∵AB=9cm,BC=14cm,CA=13cm,
∴BD=BF=(9-a)cm,CD=CE=(13-a)cm,
∵BD+CD=BC=14cm,
∴(9-a)+(13-a)=14,
解得:a=4,
即AF=4cm.
故答案为4cm.
11.15.
解析:
∵四边形ABCD的边AB、BC、CD、DA和O分别切于L、M、N、P,
∴AP=AL,BM=BL,CM=CN,DN=DP,
∴AL+BL+DN+CN=AP+BM+DP+CM,
即AB+CD=AD+BC,
∵AB=10cm,CD=5cm,
∴AB+CD =15cm,故答案为15.
12.1∶5
解析:
由题意得:S=??l?×r,即S=???×10×r,∴r:s=1:5
故答案为:1:5.
13.(1)不是;
(2)54;
(3).
解析:
解:(1)矩形的对角线相等但不垂直,
所以矩形不是奇妙四边形;
故答案为不是;
(2)
连结OB、OD,作OH⊥BD于H,如图2,则BH=DH,
∵∠BOD=2∠BCD=2×60°=120°,
∴在等腰△OBD中,∠OBD=30°,
在Rt△OBH中,∵∠OBH=30°,
∴,
∴
∴
∵四边形ABCD是奇妙四边形,
∴,
∴;
(3).
理由如下:
连结OB、OC、OA、OD,作OE⊥AD于E,如图3,
∵OE⊥AD,
∴在等腰△AOD中,,
又∵,
∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,
∴∠BAC+∠ABD=90°,
∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,
∴∠OBM=∠AOE,
在△BOM和△OAE中
∴,
∴OM=AE,
∴.
14.见解析
解析:
①DE与⊙O相切,AB=BC,DE2+CE2=CD2,∠C+∠CDE=90°
BC是⊙O的切线,有2DE=2AB等.
15.(1)证明见解析;(2).
解析:
(1)证明:∵、与相切于、.
∴,平分.
在等腰中,,平分.
∴于,即.
(2)解:连接、.
∵
∴
∴
同理:
∴.
在等腰中,.
∴.
∵与相切于.
∴.
∴.
在中,,
∴.
16.(1)证明见解析;(2)CA=6,EH=2.
解析:
分析:(1)根据切线的性质即可证明:∠CAB=∠EHB,由此即可解决问题;
(2)连接AF.由△CAF∽△CBA,推出CA2=CF?CB=36,推出CA=6,AB=,AF=,由Rt△AEF≌Rt△AEH,推出AF=AH=2,设EF=EH=x.在Rt△EHB中,可得(5﹣x)2=x2+()2,解方程即可解决问题;
详解:(1)∵AC是⊙O的切线,
∴CA⊥AB.
∵EH⊥AB,
∴∠EHB=∠CAB.
∵∠EBH=∠CBA,
∴△HBE∽△ABC.
(2)连接AF.
∵AB是直径,
∴∠AFB=90°.
∵∠C=∠C,∠CAB=∠AFC,
∴△CAF∽△CBA,
∴CA2=CF?CB=36,
∴CA=6,AB=,AF=.
∵,
∴∠EAF=∠EAH.
∵EF⊥AF,EH⊥AB,
∴EF=EH.
∵AE=AE,
∴Rt△AEF≌Rt△AEH,
∴AF=AH=2.
设EF=EH=x.在Rt△EHB中,(5﹣x)2=x2+()2,
∴x=2,
∴EH=2.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
