山东省济南市济微教育集团2020-2021学年七年级上学期第一次月考(10月)数学试题(word解析版)
文档属性
| 名称 | 山东省济南市济微教育集团2020-2021学年七年级上学期第一次月考(10月)数学试题(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 496.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 14:05:00 | ||
图片预览


文档简介
山东省济南市2020-2021学年七年级上学期第一次月考(10月)数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果向北走10米记作+10米,则-8米表示( )
A.向东走8米 B.向南走8米 C.向西走8米 D.向南走-8米
2.下列说法正确的是( )
A.数轴上右边的点表示正数,左边的点表示负数
B.距离原点越远的点,表示的数越大
C.表示-2的点离原点2个单位长度
D.数轴上表示-3和1的点相距2个单位
3.下列各组中互为相反数的是( )
A.-2与 B.-(-6)和6 C.-2与 D.与
4.下列几种说法中,正确的是( )
A.0是最小的数 B.最大的负有理数是-1
C.任何有理数的绝对值都是正数 D.0是绝对值最小的数
5.某地一天早晨的气温是-2℃,中午温度上升了12℃,半夜又下降了8℃,则半夜的气温是( )
A.-16℃ B.2℃ C.-5℃ D.9℃
6.图甲和图乙中所有的正方形都全等,将图甲的正方形放在图乙中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.① B.② C.③ D.④
7.下列不是三棱柱展开图的是( )
A. B.
C. D.
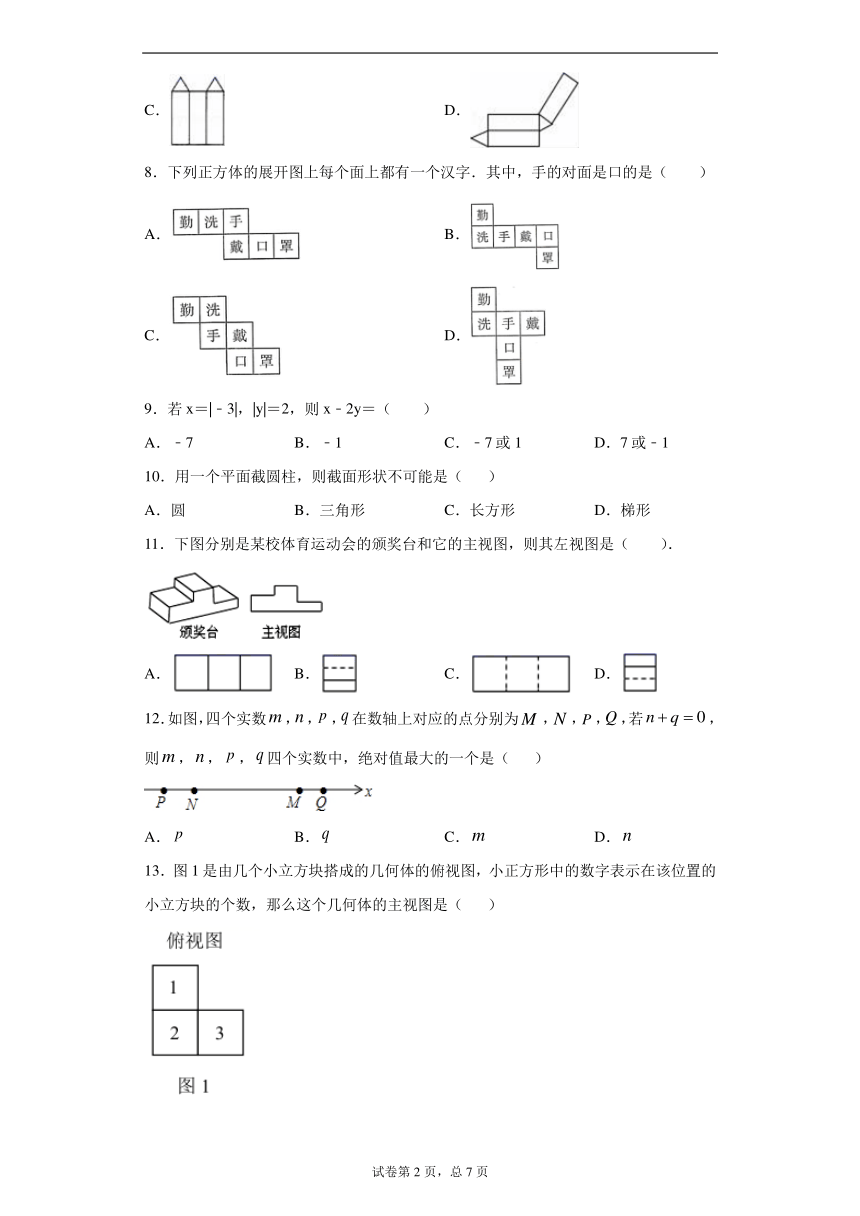
8.下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )
A. B.
C. D.
9.若x=|﹣3|,|y|=2,则x﹣2y=( )
A.﹣7 B.﹣1 C.﹣7或1 D.7或﹣1
10.用一个平面截圆柱,则截面形状不可能是( )
A.圆 B.三角形 C.长方形 D.梯形
11.下图分别是某校体育运动会的颁奖台和它的主视图,则其左视图是( ).
A. B. C. D.
12.如图,四个实数,,,在数轴上对应的点分别为,,,,若,则,,,四个实数中,绝对值最大的一个是( )
A. B. C. D.
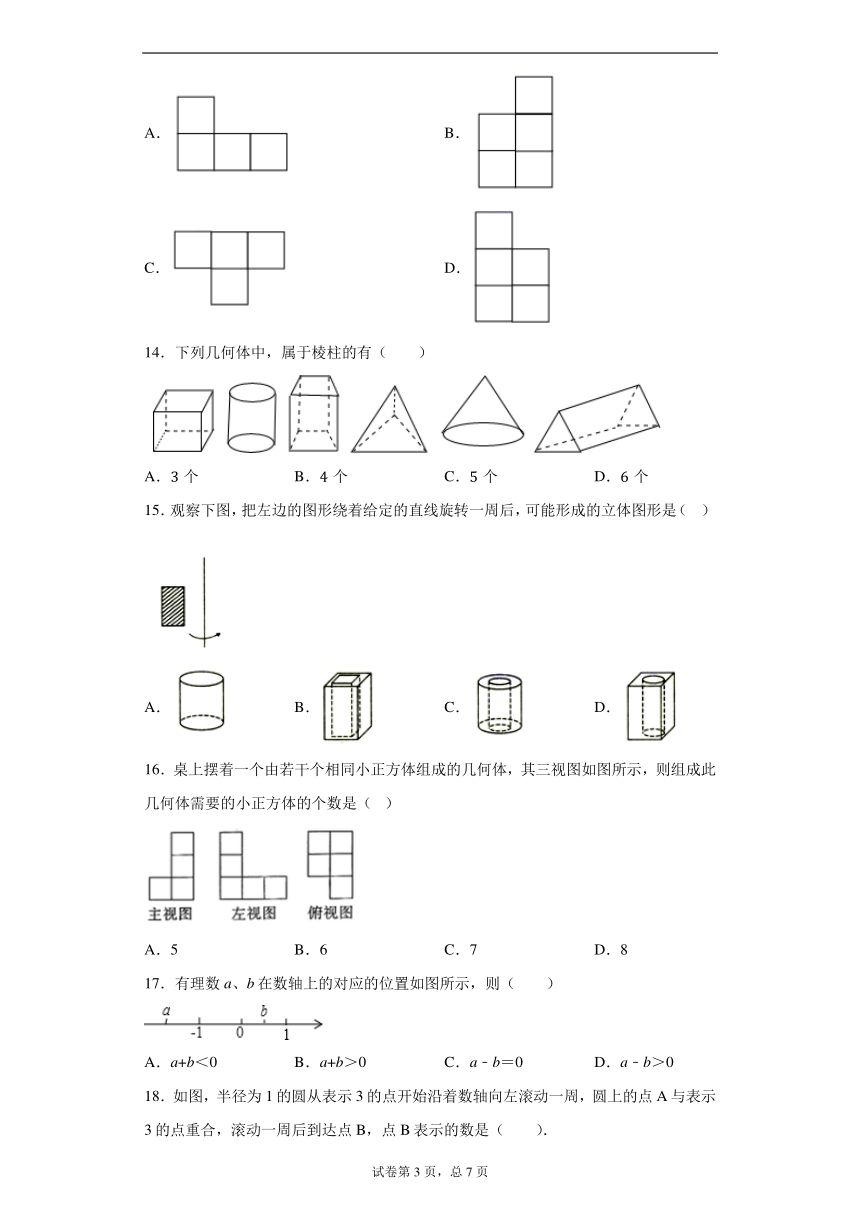
13.图1是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )
A. B.
C. D.
14.下列几何体中,属于棱柱的有( )
A.3个 B.4个 C.5个 D.6个
15.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是(? ?)
A. B. C. D.
16.桌上摆着一个由若干个相同小正方体组成的几何体,其三视图如图所示,则组成此几何体需要的小正方体的个数是( )
A.5 B.6 C.7 D.8
17.有理数a、b在数轴上的对应的位置如图所示,则( )
A.a+b<0 B.a+b>0 C.a﹣b=0 D.a﹣b>0
18.如图,半径为1的圆从表示3的点开始沿着数轴向左滚动一周,圆上的点A与表示3的点重合,滚动一周后到达点B,点B表示的数是( ).
A.-2 B.3-2 C.-3-2 D.-3+2
19.若,则,的关系是( )
A.与相等; B.与互为相反数;
C.与相等或互为相反数; D.无法确定
20.已知整数,,,,…满足下列条件,,,,...,依次类推,则a2020的值为( )
A.-1010 B.-1009 C.-2019 D.-2020
二、填空题
21.______.若,则______.
22.的相反数是______,绝对值是______.
23.甲地海拔高度是-63米,乙地比甲地高24米,则乙地______米.
24.定义运算“”的运算法则为:,则______.
25.已知,则______.
26.如图所示,将图沿虚线折起来得到一个正方体,那么“1”的对面是________(填编号).
27.如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,则________.
28.长方体的主视图和左视图如下图所示(单位:),则其府视图的面积是__________.
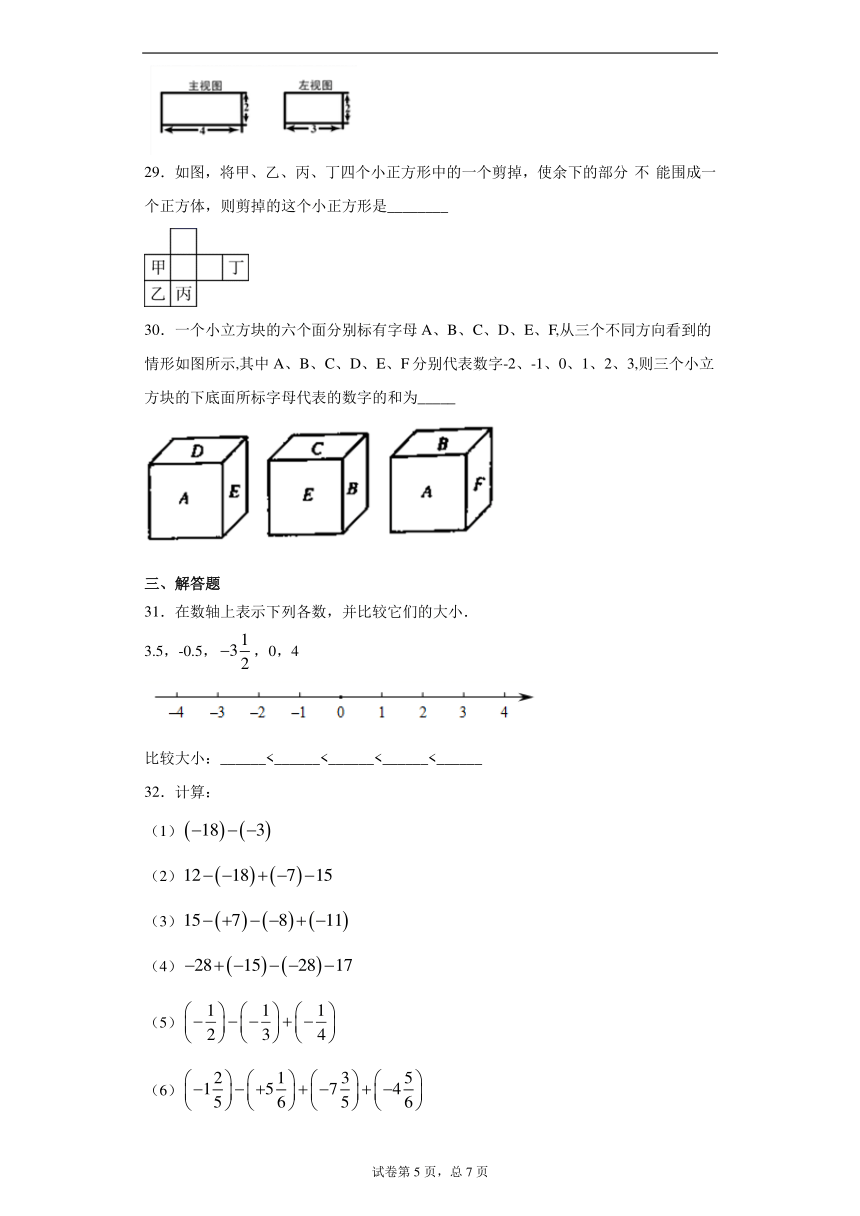
29.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分 不 能围成一个正方体,则剪掉的这个小正方形是________
30.一个小立方块的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示,其中A、B、C、D、E、F分别代表数字-2、-1、0、1、2、3,则三个小立方块的下底面所标字母代表的数字的和为_____
三、解答题
31.在数轴上表示下列各数,并比较它们的大小.
3.5,-0.5,,0,4
比较大小:______<______<______<______<______
32.计算:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
33.一个几何体由一些大小相同的小正方块儿搭建,如图是从上面看到的这个几何体的形状如图,小正方形的数字表示在该位置的小正方块儿的个数,请在网格中画出从正面和左面看到的几何体的形状图.
34.初一某班6名男生测量身高,以160cm为标准,超过的记作正数,不足的记作负数.测量结果记录如下:
学生序号
1
2
3
4
5
6
身高(cm)
165
158
164
163
157
168
差值(cm)
+5
m
+4
+3
-3
+8
(1)求m值.
(2)计算这6名同学的平均身高.
35.出租车司机王叔叔一天下午的营运全在东西的长安街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+5 -13 +10 -7 -8 +12 +4 -5
(1)将最后一名乘客送到目的地时,王叔叔距下午出车时的出发点有多远?在出发点的什么方向?
(2)若每千米汽车耗油0.6升,这天下午王叔叔共行车多少千米?耗油多少升?
36.小虫从某点O出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-10.
(1)小虫是否回到原点O?
(2)在爬行过程中,如果每爬行1厘米奖励2粒芝麻,则小虫共可得到多少粒芝麻?
37.2020年的“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩厂为满足市场需求计划每天生产5000个,由于各种原因实际每天生产量相比有出入,下表是二月份某一周的生产情况(超产为正,减产为负,单位:个)
星期
一
二
三
四
五
六
日
增减
+100
-200
+400
-100
-100
+350
+150
(1)根据记录可知前三天共生产多少个口罩?
(2)产量最多的一天比产量最少的一天多生产多少个?
(3)该口罩加工厂实行计件工资制,每生产一个口罩0.2元,本周口罩加工厂应支付工人的工资总额是金额元?
参考答案
1.B
【分析】
利用相反意义的量的相反词即可判断.
【详解】
向南走8米与向北走10米是具有相反意义的量,
向北走10米记作+10米,
-8米表示向南走8米,
故选择:B.
【点睛】
本题考查相反意义的量问题,掌握相反意义的量,会用相反词识别相反意义的量的问题是解题关键.
2.C
【详解】
略
3.C
【分析】
先化简各选项中需要化简的数,再根据相反数的定义解得即可.
【详解】
解:由仅仅只有符号不同的两个数互为相反数可得:
?2 与 ? 不互为相反数,故A错误;
由 ?(?6)=6,所以 ?(?6)与 6 相等,故B错误;
由 |?2|=2, 所以 ?2与 |?2| 互为相反数,故C正确;
由 与 ∣?∣= 不互为相反数,故D错误;
故选C.
【点睛】
本题考查的是绝对值的含义,相反数的定义,掌握以上知识是解题的关键.
4.D
【分析】
根据有理数的定义可判断A、B两项,根据绝对值的意义可判断C、D两项,进而可得答案.
【详解】
解:A、没有最小的数,故本选项说法错误,不符合题意;
B、没有最大的负有理数,故本选项说法错误,不符合题意;
C、任何有理数的绝对值都是正数或0,故本选项说法错误,不符合题意;
D、0是绝对值最小的数,故本选项说法正确,符合题意.
故选:D.
【点睛】
本题考查了有理数的定义和绝对值,属于基础题目,熟练掌握基本知识是解题的关键.
5.B
【分析】
根据题意可列出算式﹣2+12-8,再根据有理数的加减混合运算法则解答即可.
【详解】
解:半夜的气温是﹣2+12-8=2℃.
故选:B.
【点睛】
本题考查了有理数加减混合运算的应用,属于基础题目,正确列式、准确计算是解题的关键.
6.A
【分析】
由平面图形的折叠及正方体的表面展开图的特点解题.
【详解】
将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体,
故选A.
【点睛】
本题考查了展开图折叠成几何体,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意:只要有“田”字格的展开图都不是正方体的表面展开图.
7.C
【分析】
根据三棱柱的两底展开是三角形,侧面展开是三个四边形,可得答案.
【详解】
解:A、B、D中间三个长方形能围成三棱柱的侧面,两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.C围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故C不能围成三棱柱.
故选C.
【点睛】
本题考查了几何体的展开图,注意两底面是对面,展开是两个全等的三角形,侧面展开是三个矩形.
8.B
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点逐项判断即可.
【详解】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
A、手的对面是勤,所以本选项不符合题意;
B、手的对面是口,所以本选项符合题意;
C、手的对面是罩,所以本选项不符合题意;
D、手的对面是罩,所以本选项不符合题意.
故选:B.
【点睛】
本题考查了正方体相对面上的文字,属于常考题型,熟知正方体相对两个面的特征是解题的关键.
9.D
【分析】
由已知可得x=3,y=±2,再将x与y的值代入x﹣2y即可求解.
【详解】
解:∵x=|﹣3|,|y|=2,
∴x=3,y=±2,
∴x﹣2y=﹣1或7;
故选:D.
【点睛】
本题考查绝对值的性质;熟练掌握绝对值的性质,能够准确求出x与y的值是解题的关键.
10.B
【分析】
根据圆柱的特征可直接进行排除选项.
【详解】
由用一个平面截圆柱,则截面形状不可能是三角形;
故选B.
【点睛】
本题主要考查截几何体,关键是根据圆柱的特征得到可能的截面.
11.D
【分析】
根据左视图是从左边看到的图形解答即可.
【详解】
解:颁奖台从左边看是一个矩形被分为3部分,上面分线是实线,下面的分线是虚线.
故选:D
【点睛】
本题考查了由几何体判断三视图,从左边看到的图形是左视图,注意能看到的线用实线画,看不到的线用虚线画.
12.A
【分析】
根据题意可判断0在线段NQ的中点处,再根据绝对值的意义即可进行判断.
【详解】
解:因为,
所以n、q互为相反数,0在线段NQ的中点处,
所以点P距离原点的距离最远,即,,,四个实数中,绝对值最大的一个是p.
故选:A.
【点睛】
本题考查了实数与数轴以及线段的中点,正确理解题意、确定数轴上原点的位置是解题关键.
13.B
【分析】
根据各层小正方体的个数,然后判断出三视图中主视图的形状,即可得出答案;
【详解】
综合俯视图可知,主视图一共两列且左边一列有2个小正方体,右边一列有3个小正方体,
∴主视图是;
故答案选B.
【点睛】
本题主要考查了由三视图判断几何体,准确判断是解题的关键.
14.A
【解析】
根据棱柱的概念,有两个面互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.因此可知长方体,四棱柱,三棱柱是属于棱柱.
故选A.
点睛:此题主要考查了棱柱的识别,解题时,熟悉概念:有两个面互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.
15.C
【分析】
根据面动成体的原理以及空间想象力即可解答.
【详解】
解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
故选:C.
【点睛】
本题考查了点、线、面、体的关系,从运动的观点来看点动成线,线动成面,面动成体.点、线、面、体组成几何图形,点、线、面、体的运动组成了多姿多彩的图形世界.也考查学生对立体图形的空间想象能力及分析问题,解决问题的能力.
16.C
【分析】
从俯视图中可以看出最底层小正方体的个数及形状,从主视图和左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】
根据俯视图可知该组合体共3行、2列,
结合主视图和左视图知该几何体中小正方体的分布情况如图所示:
则组成此几何体需要正方体的个数是7,
故选C.
【点睛】
本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
17.A
【分析】
由数轴可得a﹣1,0b1,分别判断选项即可.
【详解】
解:根据数轴可得:a﹣1,0b1,
∴|a||b|,
A、a+b0,故A选项正确;
B、a+b0,故B选项错误;
C、a﹣b0,故C选项错误;
D、a﹣b0,故D选项错误.
故答案选A.
【点睛】
本题主要考查了数轴、有理数的运算;解题的关键是从数轴中准确获取信息,并结合有理数的运算.
18.B
【分析】
根据数轴的性质,得A点到B点的距离为圆的周长,通过求解圆的周长,即可得到答案.
【详解】
∵圆上的点A与表示3的点重合,滚动一周后到达点B
∴A点到B点的距离等于圆的周长
∵圆的半径为1
∴圆的周长为
∵半径为1的圆从表示3的点开始沿着数轴向左滚动一周
∴点A表示的数大于点B表示的数
∴B表示的数
故选:B.
【点睛】
本题考查了数轴、圆周长的知识;解题的关键是熟练掌握数轴、圆周长的的性质,从而完成求解.
19.C
【分析】
由绝对值相等的两个数可能相等也可能互为相反数即可选出答案.
【详解】
A.a与b也可能互为相反数,故A选项错误;
B.a与b也可能相等,故B选项错误;
C.绝对值相等的两个数可能相等也可能互为相反数,故C选项正确;
D.a与b的关系可以确定,故D选项错误.
故选:C.
【点睛】
本题考查绝对值的相关性质,牢记两个数的绝对值相等,则这两个数相等或互为相反数是解题关键.
20.A
【分析】
根据题意先求出前几个数的值,进而可得规律,再根据规律求解即可.
【详解】
解:,
,
,
,
,
……,
所以n为奇数时,结果等于,n为偶数时,结果等于,
所以a2020=.
故选:A.
【点睛】
本题考查了数字的变化规律,属于常考题型,根据前几个数值找到规律是解答的关键.
21.8
【分析】
根据绝对值的定义解答即可.
【详解】
解:8,若,则.
故答案为:8,.
【点睛】
本题考查了有理数的绝对值,属于基础题目,熟练掌握绝对值的定义是关键.
22.
【分析】
根据有理数的相反数与绝对值的定义解答即可.
【详解】
解:的相反数是,绝对值是.
故答案为:,.
【点睛】
本题考查了有理数的相反数与绝对值,属于应知应会题型,熟练掌握基本知识是关键.
23.-39
【分析】
根据有理数的加法的运算方法,用甲地的海拔高度加上24,求出乙地的海拔高度为多少即可.
【详解】
解:(?63)+24=-39(米)
答:乙地的海拔高度为-39米.
故答案为:-39米.
【点睛】
此题主要考查了有理数的加法,要熟练掌握,解答此题的关键是要明确:(1)同号相加,取相同符号,并把绝对值相加.(2)绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
24.-12
【分析】
根据题目的运算法则解答即可.
【详解】
解:.
故答案为:﹣12.
【点睛】
本题考查了有理数的运算,正确理解题意、掌握解答的方法是关键.
25.-2
【分析】
根据绝对值的非负性可直接进行求解.
【详解】
解:∵,
∴,
∴,
∴;
故答案为.
【点睛】
本题主要考查绝对值的非负性,熟练掌握绝对值的非负性是解题的关键.
26.5
【解析】
试题解析:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“1”与“5”是相对面,
“2”与“4”是相对面,
“3”与“6”是相对面.
故答案为5.
27.4
【分析】
利用正方体及其表面展开图的特点,根据相对面上的两个数之和为5,列出方程求出x、y、z的值,从而得到x+y+z的值.
【详解】
解:这是一个正方体的平面展开图,共有六个面,
其中面“z”与面“3”相对,面“y”与面“?2”相对,“x”与面“10”相对.
则z+3=5,y+(?2)=5,x+10=5,
解得z=2,y=7,x=?5.
故x+y+z=4.
故答案为4.
【点睛】
本题考查了正方体相对两个面.解题的关键是注意正方体的空间图形,从相对面入手,分析及解答问题.
28.
【解析】
解:∵主视图可得长方体的长与高,左视图可得长方体的宽与高,
∴长方体的长为4,宽为3,高为2,
又∵俯视图的面积=长×宽,
∴俯视图的面积=4×3=12cm2.
故答案是12.
29.丁
【分析】
能围成正方体的“一四一”,“二三一”,“三三”,“二二二”的基本形态要记牢.解题时,据此即可判断答案.
【详解】
解:将如图所示的图形剪去一个小正方形,使余下的部分不能围成一个正方体,编号为甲乙丙丁的小正方形中剪去的是丁,
故答案为:丁.
【点睛】
本题考查了展开图折叠成正方体的知识,解题关键是根据正方体的特征,或者熟记正方体的11种展开图,只要有“田”,“凹”字格的展开图都不是正方体的表面展开图.
30.-2
【分析】
根据A、B、E相邻的四个面上的字母分别确定他们各自的对立面,代入数字运算即可.
【详解】
解:由第一个和第三个图可知,A的四个相邻面分别是D、E、B、F,所以A的对立面是C;
由第二个和第三个图可知,B的四个相邻面分别是E、A、F、C,所以B的对立面是D;
综上可知三个小立方块的下底面所标字母分别为B、A、D.
其中A、B、C、D、E、F分别代表数字-2、-1、0、1、2、3, 则三个小立方块的下底面所标字母代表的数字的和为-2-1+1=-2.
故答案为-2.
【点睛】
本题考查正方形相对两个面上的文字,仔细观察图形从相邻面考虑求解是解决本题的关键.
31.图见解析,.
【分析】
先在数轴上表示出各点,然后再根据数轴的右边大于左边解答即可.
【详解】
解:各点在数轴上表示如下:
则.
故答案为:.
【点睛】
本题主要考查了数轴以及利用数轴比较有理数的大小,掌握“数轴上的数,右边的总比左边的大”是解答本题的关键.
32.(1)-15;(2)8;(3)5;(4)-32;(5);(6)-19;(7)32;(8)26
【分析】
(1)根据有理数的减法法则计算;
(2)根据有理数的加减混合运算法则计算;
(3)根据有理数的加减混合运算法则计算;
(4)根据有理数的加减混合运算法则计算;
(5)根据有理数的加减混合运算法则计算;
(6)先把原式统一为加法,再利用加法的交换律和结合律计算;
(7)先计算乘法,再计算减法;
(8)根据乘法分配律计算.
【详解】
解:(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8).
【点睛】
本题考查了有理数的运算,属于基础题目,熟练掌握运算法则是解题的关键.
33.见解析
【分析】
主视图应该有3列,看到的正方形的个数分别是2、3、4,左视图应该有2列,看到的正方形的个数分别是2、4,据此解答即可
【详解】
解:正面和左面看到的几何体的形状图如图所示:
【点睛】
本题考查了简单组合体的三视图,属于常考题型,掌握解答的方法是解题的关键.
34.(1)m的值为;(2)这6名同学的平均身高为.
【分析】
(1)用身高与作差即可得;
(2)先求出这6名同学身高的差值的平均值,再加上即可得.
【详解】
(1)由题意得:
答:m的值为;
(2)这6名同学身高的差值的平均值为:
则这6名同学的平均身高为:
答:这6名同学的平均身高为.
【点睛】
本题考查了正数与负数在生活中的应用、有理数的加减法、及除法,理解题意正确列出式子是解题关键.
35.(1)王叔叔距出发点2千米,在出发点的西面;(2)这天下午王叔叔共行车64千米,耗油38.4升
【分析】
(1)将题目中的数据相加,再根据结果判断即可;
(2)将题目中所有数据的绝对值相加即可求出共行车的路程,求得的和再乘以0.6即可求出耗油总量.
【详解】
解:(1)(千米);
答:将最后一名乘客送到目的地时,王叔叔距出发点2千米,在出发点的西面.
(2)(千米),(升).
答:这天下午王叔叔共行车64千米,耗油38.4升.
【点睛】
本题考查了正负数和有理数的加法在实际中的应用,属于常考题型,正确理解题意、熟练掌握上述知识是解题的关键.
36.(1)能回到原点;(2)共可得到108粒芝麻.
【分析】
(1)由于向右爬行的路程记为正数,向左爬行的路程为负数,所以要计算出它爬行所有数的和,而(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)=0,于是可判断回到出发点;
(2)计算所有数的绝对值得到小虫爬行的路程,再把路程乘以2得到小虫共得的芝麻.
【详解】
(1)∵(+5)+(?3)+(+10)+(?8)+(?6)+(+12)+(?10),
=5?3+10?8?6+12?10,
=5+10+12?3?8?6?10,
=27?27,
=0,
∴小虫最后可以回到出发点;
(2)(|+5|+|?3|+|+10|+|?8|+|?6|+|+12|+|?10|)×2,
=(5+3+10+8+6+12+10)×2,
=54×2,
=108,
所以小虫共可得108粒芝麻.
【点睛】
考查了正数和负数,解题的关键是掌握正数与负数的定义以及它的实际意义,在求距离时是各数的绝对值,与正负无关.
37.(1)15300个;(2)600个;(3)7120元.
【分析】
(1)把前三天的记录相加,再加上每天计划生产量,计算即可得解;
(2)根据正负数的意义确定星期三产量最多,星期二产量最少,然后用记录相减计算即可得解;
(3)求出一周记录的和,然后根据工资总额的计算方法列式计算即可得解.
【详解】
解:(1)(+100﹣200+400)+3×5000=15300(个).
故前三天共生产15300个口罩;
(2)+400﹣(﹣200)=600(个).
故产量最多的一天比产量最少的一天多生产600个;
(3)5000×7+(100﹣200+400﹣100﹣100+350+150)=35600(个),
0.2×35600=7120(元).
故本周口罩加工厂应支付工人的工资总额是7120元.
【点睛】
此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果向北走10米记作+10米,则-8米表示( )
A.向东走8米 B.向南走8米 C.向西走8米 D.向南走-8米
2.下列说法正确的是( )
A.数轴上右边的点表示正数,左边的点表示负数
B.距离原点越远的点,表示的数越大
C.表示-2的点离原点2个单位长度
D.数轴上表示-3和1的点相距2个单位
3.下列各组中互为相反数的是( )
A.-2与 B.-(-6)和6 C.-2与 D.与
4.下列几种说法中,正确的是( )
A.0是最小的数 B.最大的负有理数是-1
C.任何有理数的绝对值都是正数 D.0是绝对值最小的数
5.某地一天早晨的气温是-2℃,中午温度上升了12℃,半夜又下降了8℃,则半夜的气温是( )
A.-16℃ B.2℃ C.-5℃ D.9℃
6.图甲和图乙中所有的正方形都全等,将图甲的正方形放在图乙中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.① B.② C.③ D.④
7.下列不是三棱柱展开图的是( )
A. B.
C. D.
8.下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )
A. B.
C. D.
9.若x=|﹣3|,|y|=2,则x﹣2y=( )
A.﹣7 B.﹣1 C.﹣7或1 D.7或﹣1
10.用一个平面截圆柱,则截面形状不可能是( )
A.圆 B.三角形 C.长方形 D.梯形
11.下图分别是某校体育运动会的颁奖台和它的主视图,则其左视图是( ).
A. B. C. D.
12.如图,四个实数,,,在数轴上对应的点分别为,,,,若,则,,,四个实数中,绝对值最大的一个是( )
A. B. C. D.
13.图1是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )
A. B.
C. D.
14.下列几何体中,属于棱柱的有( )
A.3个 B.4个 C.5个 D.6个
15.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是(? ?)
A. B. C. D.
16.桌上摆着一个由若干个相同小正方体组成的几何体,其三视图如图所示,则组成此几何体需要的小正方体的个数是( )
A.5 B.6 C.7 D.8
17.有理数a、b在数轴上的对应的位置如图所示,则( )
A.a+b<0 B.a+b>0 C.a﹣b=0 D.a﹣b>0
18.如图,半径为1的圆从表示3的点开始沿着数轴向左滚动一周,圆上的点A与表示3的点重合,滚动一周后到达点B,点B表示的数是( ).
A.-2 B.3-2 C.-3-2 D.-3+2
19.若,则,的关系是( )
A.与相等; B.与互为相反数;
C.与相等或互为相反数; D.无法确定
20.已知整数,,,,…满足下列条件,,,,...,依次类推,则a2020的值为( )
A.-1010 B.-1009 C.-2019 D.-2020
二、填空题
21.______.若,则______.
22.的相反数是______,绝对值是______.
23.甲地海拔高度是-63米,乙地比甲地高24米,则乙地______米.
24.定义运算“”的运算法则为:,则______.
25.已知,则______.
26.如图所示,将图沿虚线折起来得到一个正方体,那么“1”的对面是________(填编号).
27.如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,则________.
28.长方体的主视图和左视图如下图所示(单位:),则其府视图的面积是__________.
29.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分 不 能围成一个正方体,则剪掉的这个小正方形是________
30.一个小立方块的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示,其中A、B、C、D、E、F分别代表数字-2、-1、0、1、2、3,则三个小立方块的下底面所标字母代表的数字的和为_____
三、解答题
31.在数轴上表示下列各数,并比较它们的大小.
3.5,-0.5,,0,4
比较大小:______<______<______<______<______
32.计算:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
33.一个几何体由一些大小相同的小正方块儿搭建,如图是从上面看到的这个几何体的形状如图,小正方形的数字表示在该位置的小正方块儿的个数,请在网格中画出从正面和左面看到的几何体的形状图.
34.初一某班6名男生测量身高,以160cm为标准,超过的记作正数,不足的记作负数.测量结果记录如下:
学生序号
1
2
3
4
5
6
身高(cm)
165
158
164
163
157
168
差值(cm)
+5
m
+4
+3
-3
+8
(1)求m值.
(2)计算这6名同学的平均身高.
35.出租车司机王叔叔一天下午的营运全在东西的长安街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+5 -13 +10 -7 -8 +12 +4 -5
(1)将最后一名乘客送到目的地时,王叔叔距下午出车时的出发点有多远?在出发点的什么方向?
(2)若每千米汽车耗油0.6升,这天下午王叔叔共行车多少千米?耗油多少升?
36.小虫从某点O出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-10.
(1)小虫是否回到原点O?
(2)在爬行过程中,如果每爬行1厘米奖励2粒芝麻,则小虫共可得到多少粒芝麻?
37.2020年的“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩厂为满足市场需求计划每天生产5000个,由于各种原因实际每天生产量相比有出入,下表是二月份某一周的生产情况(超产为正,减产为负,单位:个)
星期
一
二
三
四
五
六
日
增减
+100
-200
+400
-100
-100
+350
+150
(1)根据记录可知前三天共生产多少个口罩?
(2)产量最多的一天比产量最少的一天多生产多少个?
(3)该口罩加工厂实行计件工资制,每生产一个口罩0.2元,本周口罩加工厂应支付工人的工资总额是金额元?
参考答案
1.B
【分析】
利用相反意义的量的相反词即可判断.
【详解】
向南走8米与向北走10米是具有相反意义的量,
向北走10米记作+10米,
-8米表示向南走8米,
故选择:B.
【点睛】
本题考查相反意义的量问题,掌握相反意义的量,会用相反词识别相反意义的量的问题是解题关键.
2.C
【详解】
略
3.C
【分析】
先化简各选项中需要化简的数,再根据相反数的定义解得即可.
【详解】
解:由仅仅只有符号不同的两个数互为相反数可得:
?2 与 ? 不互为相反数,故A错误;
由 ?(?6)=6,所以 ?(?6)与 6 相等,故B错误;
由 |?2|=2, 所以 ?2与 |?2| 互为相反数,故C正确;
由 与 ∣?∣= 不互为相反数,故D错误;
故选C.
【点睛】
本题考查的是绝对值的含义,相反数的定义,掌握以上知识是解题的关键.
4.D
【分析】
根据有理数的定义可判断A、B两项,根据绝对值的意义可判断C、D两项,进而可得答案.
【详解】
解:A、没有最小的数,故本选项说法错误,不符合题意;
B、没有最大的负有理数,故本选项说法错误,不符合题意;
C、任何有理数的绝对值都是正数或0,故本选项说法错误,不符合题意;
D、0是绝对值最小的数,故本选项说法正确,符合题意.
故选:D.
【点睛】
本题考查了有理数的定义和绝对值,属于基础题目,熟练掌握基本知识是解题的关键.
5.B
【分析】
根据题意可列出算式﹣2+12-8,再根据有理数的加减混合运算法则解答即可.
【详解】
解:半夜的气温是﹣2+12-8=2℃.
故选:B.
【点睛】
本题考查了有理数加减混合运算的应用,属于基础题目,正确列式、准确计算是解题的关键.
6.A
【分析】
由平面图形的折叠及正方体的表面展开图的特点解题.
【详解】
将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体,
故选A.
【点睛】
本题考查了展开图折叠成几何体,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意:只要有“田”字格的展开图都不是正方体的表面展开图.
7.C
【分析】
根据三棱柱的两底展开是三角形,侧面展开是三个四边形,可得答案.
【详解】
解:A、B、D中间三个长方形能围成三棱柱的侧面,两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.C围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故C不能围成三棱柱.
故选C.
【点睛】
本题考查了几何体的展开图,注意两底面是对面,展开是两个全等的三角形,侧面展开是三个矩形.
8.B
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点逐项判断即可.
【详解】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
A、手的对面是勤,所以本选项不符合题意;
B、手的对面是口,所以本选项符合题意;
C、手的对面是罩,所以本选项不符合题意;
D、手的对面是罩,所以本选项不符合题意.
故选:B.
【点睛】
本题考查了正方体相对面上的文字,属于常考题型,熟知正方体相对两个面的特征是解题的关键.
9.D
【分析】
由已知可得x=3,y=±2,再将x与y的值代入x﹣2y即可求解.
【详解】
解:∵x=|﹣3|,|y|=2,
∴x=3,y=±2,
∴x﹣2y=﹣1或7;
故选:D.
【点睛】
本题考查绝对值的性质;熟练掌握绝对值的性质,能够准确求出x与y的值是解题的关键.
10.B
【分析】
根据圆柱的特征可直接进行排除选项.
【详解】
由用一个平面截圆柱,则截面形状不可能是三角形;
故选B.
【点睛】
本题主要考查截几何体,关键是根据圆柱的特征得到可能的截面.
11.D
【分析】
根据左视图是从左边看到的图形解答即可.
【详解】
解:颁奖台从左边看是一个矩形被分为3部分,上面分线是实线,下面的分线是虚线.
故选:D
【点睛】
本题考查了由几何体判断三视图,从左边看到的图形是左视图,注意能看到的线用实线画,看不到的线用虚线画.
12.A
【分析】
根据题意可判断0在线段NQ的中点处,再根据绝对值的意义即可进行判断.
【详解】
解:因为,
所以n、q互为相反数,0在线段NQ的中点处,
所以点P距离原点的距离最远,即,,,四个实数中,绝对值最大的一个是p.
故选:A.
【点睛】
本题考查了实数与数轴以及线段的中点,正确理解题意、确定数轴上原点的位置是解题关键.
13.B
【分析】
根据各层小正方体的个数,然后判断出三视图中主视图的形状,即可得出答案;
【详解】
综合俯视图可知,主视图一共两列且左边一列有2个小正方体,右边一列有3个小正方体,
∴主视图是;
故答案选B.
【点睛】
本题主要考查了由三视图判断几何体,准确判断是解题的关键.
14.A
【解析】
根据棱柱的概念,有两个面互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.因此可知长方体,四棱柱,三棱柱是属于棱柱.
故选A.
点睛:此题主要考查了棱柱的识别,解题时,熟悉概念:有两个面互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.
15.C
【分析】
根据面动成体的原理以及空间想象力即可解答.
【详解】
解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
故选:C.
【点睛】
本题考查了点、线、面、体的关系,从运动的观点来看点动成线,线动成面,面动成体.点、线、面、体组成几何图形,点、线、面、体的运动组成了多姿多彩的图形世界.也考查学生对立体图形的空间想象能力及分析问题,解决问题的能力.
16.C
【分析】
从俯视图中可以看出最底层小正方体的个数及形状,从主视图和左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】
根据俯视图可知该组合体共3行、2列,
结合主视图和左视图知该几何体中小正方体的分布情况如图所示:
则组成此几何体需要正方体的个数是7,
故选C.
【点睛】
本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
17.A
【分析】
由数轴可得a﹣1,0b1,分别判断选项即可.
【详解】
解:根据数轴可得:a﹣1,0b1,
∴|a||b|,
A、a+b0,故A选项正确;
B、a+b0,故B选项错误;
C、a﹣b0,故C选项错误;
D、a﹣b0,故D选项错误.
故答案选A.
【点睛】
本题主要考查了数轴、有理数的运算;解题的关键是从数轴中准确获取信息,并结合有理数的运算.
18.B
【分析】
根据数轴的性质,得A点到B点的距离为圆的周长,通过求解圆的周长,即可得到答案.
【详解】
∵圆上的点A与表示3的点重合,滚动一周后到达点B
∴A点到B点的距离等于圆的周长
∵圆的半径为1
∴圆的周长为
∵半径为1的圆从表示3的点开始沿着数轴向左滚动一周
∴点A表示的数大于点B表示的数
∴B表示的数
故选:B.
【点睛】
本题考查了数轴、圆周长的知识;解题的关键是熟练掌握数轴、圆周长的的性质,从而完成求解.
19.C
【分析】
由绝对值相等的两个数可能相等也可能互为相反数即可选出答案.
【详解】
A.a与b也可能互为相反数,故A选项错误;
B.a与b也可能相等,故B选项错误;
C.绝对值相等的两个数可能相等也可能互为相反数,故C选项正确;
D.a与b的关系可以确定,故D选项错误.
故选:C.
【点睛】
本题考查绝对值的相关性质,牢记两个数的绝对值相等,则这两个数相等或互为相反数是解题关键.
20.A
【分析】
根据题意先求出前几个数的值,进而可得规律,再根据规律求解即可.
【详解】
解:,
,
,
,
,
……,
所以n为奇数时,结果等于,n为偶数时,结果等于,
所以a2020=.
故选:A.
【点睛】
本题考查了数字的变化规律,属于常考题型,根据前几个数值找到规律是解答的关键.
21.8
【分析】
根据绝对值的定义解答即可.
【详解】
解:8,若,则.
故答案为:8,.
【点睛】
本题考查了有理数的绝对值,属于基础题目,熟练掌握绝对值的定义是关键.
22.
【分析】
根据有理数的相反数与绝对值的定义解答即可.
【详解】
解:的相反数是,绝对值是.
故答案为:,.
【点睛】
本题考查了有理数的相反数与绝对值,属于应知应会题型,熟练掌握基本知识是关键.
23.-39
【分析】
根据有理数的加法的运算方法,用甲地的海拔高度加上24,求出乙地的海拔高度为多少即可.
【详解】
解:(?63)+24=-39(米)
答:乙地的海拔高度为-39米.
故答案为:-39米.
【点睛】
此题主要考查了有理数的加法,要熟练掌握,解答此题的关键是要明确:(1)同号相加,取相同符号,并把绝对值相加.(2)绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
24.-12
【分析】
根据题目的运算法则解答即可.
【详解】
解:.
故答案为:﹣12.
【点睛】
本题考查了有理数的运算,正确理解题意、掌握解答的方法是关键.
25.-2
【分析】
根据绝对值的非负性可直接进行求解.
【详解】
解:∵,
∴,
∴,
∴;
故答案为.
【点睛】
本题主要考查绝对值的非负性,熟练掌握绝对值的非负性是解题的关键.
26.5
【解析】
试题解析:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“1”与“5”是相对面,
“2”与“4”是相对面,
“3”与“6”是相对面.
故答案为5.
27.4
【分析】
利用正方体及其表面展开图的特点,根据相对面上的两个数之和为5,列出方程求出x、y、z的值,从而得到x+y+z的值.
【详解】
解:这是一个正方体的平面展开图,共有六个面,
其中面“z”与面“3”相对,面“y”与面“?2”相对,“x”与面“10”相对.
则z+3=5,y+(?2)=5,x+10=5,
解得z=2,y=7,x=?5.
故x+y+z=4.
故答案为4.
【点睛】
本题考查了正方体相对两个面.解题的关键是注意正方体的空间图形,从相对面入手,分析及解答问题.
28.
【解析】
解:∵主视图可得长方体的长与高,左视图可得长方体的宽与高,
∴长方体的长为4,宽为3,高为2,
又∵俯视图的面积=长×宽,
∴俯视图的面积=4×3=12cm2.
故答案是12.
29.丁
【分析】
能围成正方体的“一四一”,“二三一”,“三三”,“二二二”的基本形态要记牢.解题时,据此即可判断答案.
【详解】
解:将如图所示的图形剪去一个小正方形,使余下的部分不能围成一个正方体,编号为甲乙丙丁的小正方形中剪去的是丁,
故答案为:丁.
【点睛】
本题考查了展开图折叠成正方体的知识,解题关键是根据正方体的特征,或者熟记正方体的11种展开图,只要有“田”,“凹”字格的展开图都不是正方体的表面展开图.
30.-2
【分析】
根据A、B、E相邻的四个面上的字母分别确定他们各自的对立面,代入数字运算即可.
【详解】
解:由第一个和第三个图可知,A的四个相邻面分别是D、E、B、F,所以A的对立面是C;
由第二个和第三个图可知,B的四个相邻面分别是E、A、F、C,所以B的对立面是D;
综上可知三个小立方块的下底面所标字母分别为B、A、D.
其中A、B、C、D、E、F分别代表数字-2、-1、0、1、2、3, 则三个小立方块的下底面所标字母代表的数字的和为-2-1+1=-2.
故答案为-2.
【点睛】
本题考查正方形相对两个面上的文字,仔细观察图形从相邻面考虑求解是解决本题的关键.
31.图见解析,.
【分析】
先在数轴上表示出各点,然后再根据数轴的右边大于左边解答即可.
【详解】
解:各点在数轴上表示如下:
则.
故答案为:.
【点睛】
本题主要考查了数轴以及利用数轴比较有理数的大小,掌握“数轴上的数,右边的总比左边的大”是解答本题的关键.
32.(1)-15;(2)8;(3)5;(4)-32;(5);(6)-19;(7)32;(8)26
【分析】
(1)根据有理数的减法法则计算;
(2)根据有理数的加减混合运算法则计算;
(3)根据有理数的加减混合运算法则计算;
(4)根据有理数的加减混合运算法则计算;
(5)根据有理数的加减混合运算法则计算;
(6)先把原式统一为加法,再利用加法的交换律和结合律计算;
(7)先计算乘法,再计算减法;
(8)根据乘法分配律计算.
【详解】
解:(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8).
【点睛】
本题考查了有理数的运算,属于基础题目,熟练掌握运算法则是解题的关键.
33.见解析
【分析】
主视图应该有3列,看到的正方形的个数分别是2、3、4,左视图应该有2列,看到的正方形的个数分别是2、4,据此解答即可
【详解】
解:正面和左面看到的几何体的形状图如图所示:
【点睛】
本题考查了简单组合体的三视图,属于常考题型,掌握解答的方法是解题的关键.
34.(1)m的值为;(2)这6名同学的平均身高为.
【分析】
(1)用身高与作差即可得;
(2)先求出这6名同学身高的差值的平均值,再加上即可得.
【详解】
(1)由题意得:
答:m的值为;
(2)这6名同学身高的差值的平均值为:
则这6名同学的平均身高为:
答:这6名同学的平均身高为.
【点睛】
本题考查了正数与负数在生活中的应用、有理数的加减法、及除法,理解题意正确列出式子是解题关键.
35.(1)王叔叔距出发点2千米,在出发点的西面;(2)这天下午王叔叔共行车64千米,耗油38.4升
【分析】
(1)将题目中的数据相加,再根据结果判断即可;
(2)将题目中所有数据的绝对值相加即可求出共行车的路程,求得的和再乘以0.6即可求出耗油总量.
【详解】
解:(1)(千米);
答:将最后一名乘客送到目的地时,王叔叔距出发点2千米,在出发点的西面.
(2)(千米),(升).
答:这天下午王叔叔共行车64千米,耗油38.4升.
【点睛】
本题考查了正负数和有理数的加法在实际中的应用,属于常考题型,正确理解题意、熟练掌握上述知识是解题的关键.
36.(1)能回到原点;(2)共可得到108粒芝麻.
【分析】
(1)由于向右爬行的路程记为正数,向左爬行的路程为负数,所以要计算出它爬行所有数的和,而(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)=0,于是可判断回到出发点;
(2)计算所有数的绝对值得到小虫爬行的路程,再把路程乘以2得到小虫共得的芝麻.
【详解】
(1)∵(+5)+(?3)+(+10)+(?8)+(?6)+(+12)+(?10),
=5?3+10?8?6+12?10,
=5+10+12?3?8?6?10,
=27?27,
=0,
∴小虫最后可以回到出发点;
(2)(|+5|+|?3|+|+10|+|?8|+|?6|+|+12|+|?10|)×2,
=(5+3+10+8+6+12+10)×2,
=54×2,
=108,
所以小虫共可得108粒芝麻.
【点睛】
考查了正数和负数,解题的关键是掌握正数与负数的定义以及它的实际意义,在求距离时是各数的绝对值,与正负无关.
37.(1)15300个;(2)600个;(3)7120元.
【分析】
(1)把前三天的记录相加,再加上每天计划生产量,计算即可得解;
(2)根据正负数的意义确定星期三产量最多,星期二产量最少,然后用记录相减计算即可得解;
(3)求出一周记录的和,然后根据工资总额的计算方法列式计算即可得解.
【详解】
解:(1)(+100﹣200+400)+3×5000=15300(个).
故前三天共生产15300个口罩;
(2)+400﹣(﹣200)=600(个).
故产量最多的一天比产量最少的一天多生产600个;
(3)5000×7+(100﹣200+400﹣100﹣100+350+150)=35600(个),
0.2×35600=7120(元).
故本周口罩加工厂应支付工人的工资总额是7120元.
【点睛】
此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
同课章节目录
