山东省济南市第二十九中学2020-2021学年七年级上学期阶段性评估测试数学试题(Word版含解析)
文档属性
| 名称 | 山东省济南市第二十九中学2020-2021学年七年级上学期阶段性评估测试数学试题(Word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 332.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览





文档简介
山东省济南市第二十九中学2020-2021学年七年级上学期阶段性评估测试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
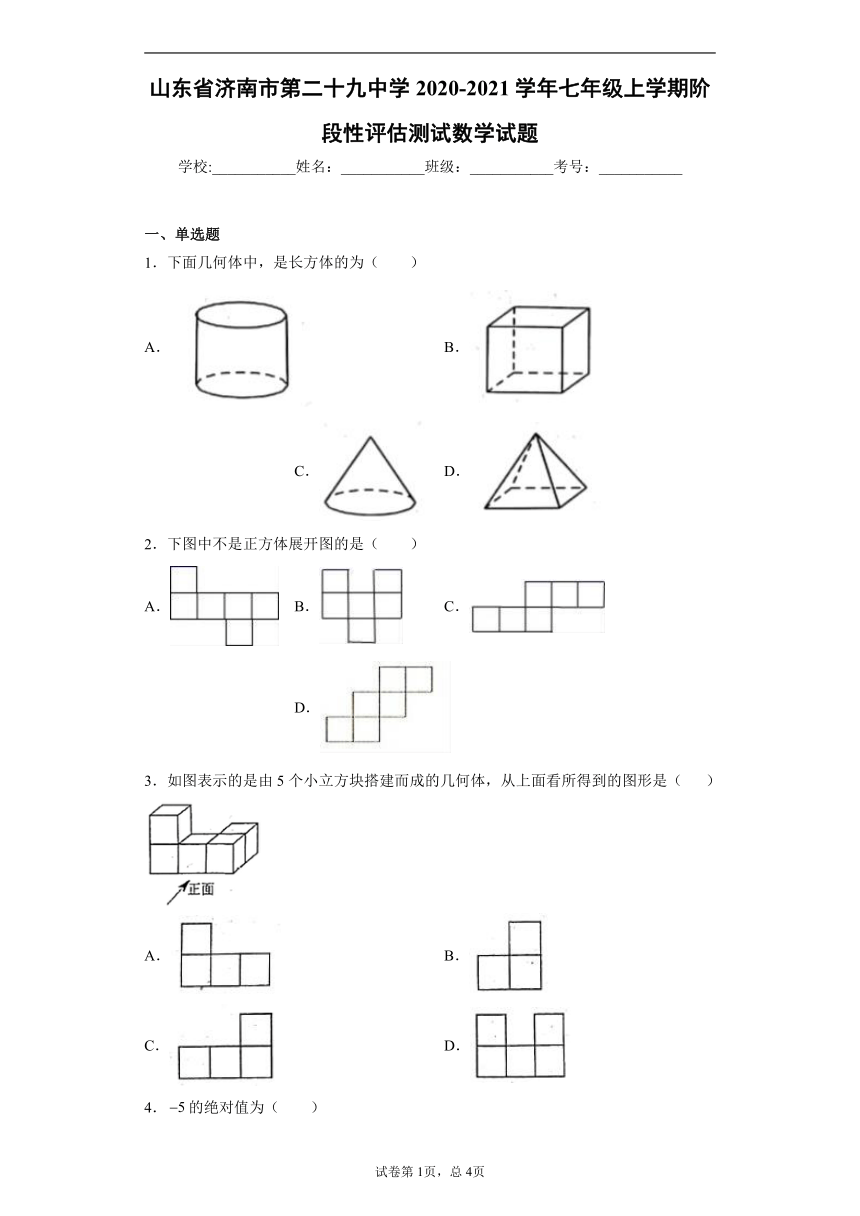
1.下面几何体中,是长方体的为( )
A. B. C. D.
2.下图中不是正方体展开图的是( )
A. B. C. D.
3.如图表示的是由5个小立方块搭建而成的几何体,从上面看所得到的图形是( )
A. B.
C. D.
4.的绝对值为( )
A. B.5 C. D.
5.规定向北为正,某人走了米,又继续走了米,那么,他实际上( )
A.向北走了15米 B.向南走了15米 C.向北走了5米 D.向南走了5米
6.数轴上的点M对应的数是-2,那么将点M向右移动4个单位长度,此时点M表示的数是( ????)
A.-6 B.2 C.-6或2 D.都不正确
7.用一个平面去截正方体,截面的形状不可能是( )
A.四边形 B.五边形 C.六边形 D.七边形
8.某种速冻水饺的储藏温度是℃,四个冷藏室的温度如下,则不适合储藏此种水饺的是( )
A.-17℃ B.-22℃ C.-18℃ D.-19℃
9.我市2015年某一天的最高气温为8℃,最低气温为-2℃,那么这天的最高气温比最低气温高
A.-10℃ B.-6℃ C.6℃ D.10℃
10.设a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,则a + b + c 等于( )
A.-1 B.0 C.1 D.2
11.若如图的平面展开图折叠成正方体后,相对面上两个数都互为相反数,则a+b=( )
A.5 B.4 C.-5 D.-4
12.若|m|=5,|n|=7,m+n<0,则m﹣n的值是( )
A.﹣12或﹣2 B.﹣2或12 C.12或2 D.2或﹣12
二、填空题
13.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说______.
14.如图是某几何体的展开图,那么这个几何体是________.
15.将一个长方体截去一个角得到一个如图所示的新几何体,这个新几何体有_____个面.
16.比较大小: _____(填“>”“<”或“=”).
17.数轴上,点B在点A的右边,已知点A表示的数是﹣2,且AB=5.那么点B表示的数是_____.
18.在数轴上,点到原点的距离等于,点所表示的数是_________
三、解答题
19.如图,上面一行是一些具体的实物图形,下面一行是一些立体图形,试用线连接立体图形和类似的实物图形.
20.如图所示的几何体是由几个相形状同的正方体搭成的,请画出这个几何体的从正面、从左面、从上面看到的形状图.
几何体
从正面看
从左面看
从上面看
21.如图是由小正方形组成的图,请你用三种方法分别在下图中添画两个小正方形,使它能成为正方体的表面展开图.
22.把下列各数填在相应的大括号里.
+2019,-3.14,-4,-,6%,0,32
(1)正整数:{ }
(2)整数:{ }
(3)正分数:{ }
(4)负分数:{ }
23.计算:
(1)(﹣25)+(﹣35); (2)(﹣12)+(+3);
(3)(+8)+(﹣7); (4)0+(﹣7).
(5); (6);
(7); (8) .
24.在数轴上表示下列各数,并用“>”连接起来.
3,-4,,0,-1,1.
25.(1)计算: (2);
26.已知,.
(1)直接写出a、b的值;
(2)若a、b异号,求a-b的值.
27.检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A地出发,到收工时,行走记录为(单位:千米):+8,﹣9,+4,+7,﹣2,﹣10,+18,﹣3,+7,+4.回答下列问题:
(1)收工地点在A地的哪个方向?距A地多少千米?
(2)若每千米耗油0.3升,那么从A地出发到收工地点,共耗油多少升?
参考答案
1.B
【分析】
根据几何体的特征进行判断即可.
【详解】
A选项为圆柱,B选项为长方体,C选项为圆锥,D选项为四棱锥.
故选:B.
【点睛】
考查立体图形的认识,掌握立体图形的特征是解题的关键.
2.B
【分析】
依据正方体的展开图的基本类型可对A、C、D选项作出判断;
依据正方体的展开图中不能出现“凹”和“田”字型可对选项B作出判断.
【详解】
根据正方体表面展开图的特点可知:
A选项图属于“1—4—1”型,是正方体展开图;
B选项图属于“凹”字型,不是正方体的展开图;
C选项图属于“3—3”型,是正方体展开图;
D选项图属于“2—2—2”型,是正方体展开图.
故选B.
【点睛】
本题主要考查的是几何体的展开图,掌握正方体的展开图的特点是解题的关键.
3.C
【分析】
从上面看得到从左往右3列,正方形的个数依次为1,1,2,依此判别出图形即可.
【详解】
从上面看有三列,第一列是1个正方体,中间一列是1个正方体,第三列是2个正方体,
故选:C.
【点睛】
本题主要考查了简单几何体的三视图,关键是掌握三视图的定义,从上面看它得到的平面图形是俯视图.
4.B
【分析】
一个负数的绝对值是它的相反数,据此解题.
【详解】
故选:B.
【点睛】
本题考查绝对值的化简,是基础考点,难度容易,掌握绝对值的代数意义、绝对值的几何意义是解题关键.
5.D
【分析】
根据题意列出算式,再结合正负数的意义解答即可.
【详解】
解:因为规定向北为正,米,
所以他实际上向南走了5米.
故选:D.
【点睛】
本题考查了正负数和有理数加法在实际中的应用,属于常见题型,正确理解题意、熟练掌握基本知识是解题的关键.
6.B
【解析】
考点:数轴.
专题:阅读型.
分析:根据数轴上表示的数左减右加的原则计算即可.
解答:
∵数轴上的点M对应的数是-2,
∴将点M向右移动4个单位长度,此时点M表示的数是-2+4=2.故选B.
点评:本题考查的是数轴的定义及数轴上两点之间的距离公式,属较简单题目.
7.D
【分析】
正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此截面的形状可能是:三角形、四边形、五边形、六边形.根据此判断即可.
【详解】
用平面去截正方体时最多与六个面相交得六边形,因此截面的形状可能是:三角形、四边形、五边形、六边形,不可能是七边形.
故选D.
【点睛】
本题考查的是几何体的截面,解答本题的关键是认识几何体的截面只是几何体的其中一个方面的体现,同一个几何体可能会有不同的截面,不同的几何体也可能会有相同的截面.
8.B
【分析】
根据有理数的加减运算,可得温度范围,根据温度范围,可得答案.
【详解】
解:?18?2=?20℃,?18+2=?16℃,
温度范围:?20℃至?16℃,
A、?20℃<?17℃<?16℃,故A适合储藏此种水饺;
B、?22℃<?20℃,故B不适合储藏此种水饺;
C、?20℃<?18℃<?16℃,故C适合储藏此种水饺;
D、?20℃<?19℃<?16℃,故D适合储藏此种水饺;
故选:B.
【点睛】
本题考查了正数和负数,有理数的加法运算是解题关键,先算出适合温度的范围,再选出不适合的温度.
9.D
【分析】
依据题意列出算式,然后根据减法法则计算即可.
【详解】
℃.
故选:D.
【点睛】
本题主要考查了有理数的减法在实际生活中的应用,掌握有理数的减法法则是解题的关键.
10.B
【分析】
最小的正整数是1,最大的负整数是-1,绝对值最小的有理数是0,根据代数式计算即可.
【详解】
由题意得:a=1,b=-1,c=0,
则a + b + c=1+(-1)+0=0,
故选B.
【点睛】
此题考查了有理数的加减,此题的关键是知道最大的正整数是1,最大的负整数是-1,绝对值最小的有理数是0.
11.D
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,可得到b值,再利用正方体及其表面展开图的特点求出a,然后代入代数式进行计算即可.
【详解】
解:这是一个正方体的平面展开图,共有六个面,其中面“a”与面“1”相对,面“b”与面“3”相对,“2”与面“-2”相对.
因为相对面上两个数都互为相反数,
所以a=-1,b=-3,
故a+b=-4,选D.
【点睛】
注意正方体的空间图形,从相对面入手,分析及解答问题.
12.C
【分析】
根据题意,利用绝对值的意义求出m与n的值,再代入所求式子计算即可.
【详解】
解:∵|m|=5,|n|=7,且m+n<0,
∴m=5,n=﹣7;m=﹣5,n=﹣7,
可得m﹣n=12或2,
则m﹣n的值是12或2.
故选:C.
【点睛】
本题考查了绝对值的意义,掌握绝对值的意义求值是关键.
13.线动成面
【分析】
利用雨刷可看成线,扇面是面,即可求出答案.
【详解】
汽车的雨刷在挡风玻璃上画出一个扇面,这说明线动成面的数学原理.
故答案为:线动成面.
【点睛】
本题考查了点,线,面、体,此题较简单,解题时要灵活应用点、线、面、体之间的关系.
14.圆柱
【解析】
∵展开图中是由两个圆和一个矩形组成的,
∴该展开图对应的几何体是圆柱.
故答案是“圆柱”.
15.7
【分析】
观察图形可知,新几何体与原长方体比较,增加一个面,由此即可作答.
【详解】
解:长方体截去一角变成一个如图的新几何体,这个新几何体有7个面.
故答案为:7.
【点睛】
本题考查了截一个几何体.能比较新几何体与原长方体,得出面数的变化情况是解题关键.
16.<
【分析】
根据正数大于0,0大于负数,正数大于负数,可解答.
【详解】
∵-5是负数,3是正数;
∴-5<3;
故答案为:<.
【点睛】
本题考查了有理数大小的比较,牢记正数大于0,0大于负数,正数大于负数.
17.3.
【分析】
根据数轴表示数的意义,在点A的右边,到点A距离为5的点所表示的数为3.
【详解】
解:﹣2+5=3,
故答案为:3.
【点睛】
本题考查数轴表示数的意义和方法,在数轴表示的数右边总比左边的大.
18.3或-3
【分析】
与原点距离为3的点有两个,分别在原点的左边和右边,左边用减法,右边用加法计算即可.
【详解】
解:当点A在原点左边时,为0-3=-3;
当点A在原点右边时为3-0=3.
故答案为:3或-3.
【点睛】
本题主要考查了数的绝对值的几何意义.注意:在数轴上与一个点的距离为a的数有2个,在该点的左边和右边各一个.
19.解:如图所示.
【解析】
分析:上面第一个物体是一个足球,由一个完整的曲面组成,应与下面第四个图形球体连接;
上面第二个物体是一个柱体,由两个圆和一个曲面组成,应与下面第三个图形圆柱连接;
上面第三个物体类似椎体,由一个曲面和一个圆组成,应与下面第二个图形圆锥连接;
上面第四个物体是金字塔,由四个三角形组成,应与下面第五个图形三棱锥连接;
上面第五个物体由六个面组成,每个面都是正方形,应与下面第一个图形正方体连接.
详解:如图所示.
点睛:本题考查了认识立体图形,熟练掌握常见几何体的形状与实际问题的关系是解题的关键.
20.见解析
【分析】
根据题意画出不同角度的图形即可.
【详解】
如图所示:
几何体
从正面看
从左面看
从上面看
【点睛】
21.
【分析】
按照正方体及其表面展开图的特点分析作出图形即可.
【详解】
正方体有11种展开图,如下
??
根据正方体的11种展开图,题中的图可用如下三种方法方法作出:
故答案为
【点睛】
本题考查正方体的表面展开图,解题的关键是熟练掌握正方体的11种展开图.
22.(1)+2019,32;(2)+2019,-4,0,32;(3)6%;(4)-3.14,-.
【分析】
根据有理数分类解答即可。
【详解】
(1)正整数:+2019,32
(2)整数:+2019,-4,0,32
(3)正分数:6%
(4)负分数:-3.14,-.
【点睛】
关键在于掌握有理数的分类,特别是0的处理,0是整数,但既不是正数也不是负数.
23.(1)-60;(2)-9;(3)1;(4)-7;(5)-12;(6)8.8;(7);(8)3.2
【分析】
(1)原式利用同号两数相加的法则计算即可得到结果;
(2)原式利用异号两数相加的法则计算即可得到结果;
(3)原式利用异号两数相加的法则计算即可得到结果;
(4)原式利用0与任何数相加得这个数即可得到结果;
(5)原式利用减法法则计算即可得到结果;
(6)原式利用减法法则计算即可得到结果;
(7)原式利用减法法则计算即可得到结果;
(8)原式利用减法法则计算即可得到结果.
【详解】
(1)(﹣25)+(﹣35)=﹣(25+35)=﹣60;
(2)(﹣12)+(+3)=﹣(12﹣3)=﹣9;
(3)(+8)+(﹣7)=+(8﹣7)=1;
(4)0+(﹣7)=﹣7;
(5);
(6);
(7)=;
(8)=3.2.
【点睛】
本题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.
24.见解析,3>1>0>-1>-2>-4
【分析】
先在数轴上表示各个数,再比较即可.
【详解】
解:在数轴上表示如图示,
3>1>0>-1>-2>-4,
【点睛】
本题考查的是在数轴上表示有理数,利用数轴判断有理数的大小.
25.(1)-5;(2)1
【分析】
(1)根据有理数的加减运算法则计算即可;
(2)根据有理数的加减运算法则计算即可.
【详解】
(1)
;
(2)
.
【点睛】
本题主要考查了有理数的加减混合运算,熟记有理数的加减法法则是解答本题的关键.
26.(1),;(2)14或-14.
【分析】
(1)根据绝对值的意义直接写出即可;
(2)先由(1)题确定a、b异号时的值,再代入计算即可.
【详解】
解:(1),;
(2)因为a、b异号,所以当a=8时,b=-6,此时;当a=-8时,b=6,此时;
所以a-b=14或-14.
【点睛】
本题考查了绝对值的意义和有理数的减法,属于基础题型,解答(2)题时需要分类讨论.
27.(1)收工时在A地的东边,距A地24千米;(2)21.6升.
【分析】
(1)向东为正,向西为负,将行走记录相加,如果是正数,检修小组在A地东边;如果是负数,检修小组在A地西边;
(2)将每次记录的绝对值相加计算出总路程,然后乘以每千米耗油量即可.
【详解】
解:(1)+8﹣9+4+7﹣2﹣10+18﹣3+7+4=24,
∴收工地点在A地的东边,距A地24千米;
(2)|+8|+|﹣9|+|+4|+|+7|+|﹣2|+|﹣10|+|+18|+|﹣3|+|+7|+|+4|=72(千米),
72×0.3=21.6(升),
答:若每千米耗油0.3升,从A地出发到收工时,共耗油21.6升.
【点睛】
本题考查了有理数加法的实际应用以及正数和负数在实际生活中的应用,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下面几何体中,是长方体的为( )
A. B. C. D.
2.下图中不是正方体展开图的是( )
A. B. C. D.
3.如图表示的是由5个小立方块搭建而成的几何体,从上面看所得到的图形是( )
A. B.
C. D.
4.的绝对值为( )
A. B.5 C. D.
5.规定向北为正,某人走了米,又继续走了米,那么,他实际上( )
A.向北走了15米 B.向南走了15米 C.向北走了5米 D.向南走了5米
6.数轴上的点M对应的数是-2,那么将点M向右移动4个单位长度,此时点M表示的数是( ????)
A.-6 B.2 C.-6或2 D.都不正确
7.用一个平面去截正方体,截面的形状不可能是( )
A.四边形 B.五边形 C.六边形 D.七边形
8.某种速冻水饺的储藏温度是℃,四个冷藏室的温度如下,则不适合储藏此种水饺的是( )
A.-17℃ B.-22℃ C.-18℃ D.-19℃
9.我市2015年某一天的最高气温为8℃,最低气温为-2℃,那么这天的最高气温比最低气温高
A.-10℃ B.-6℃ C.6℃ D.10℃
10.设a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,则a + b + c 等于( )
A.-1 B.0 C.1 D.2
11.若如图的平面展开图折叠成正方体后,相对面上两个数都互为相反数,则a+b=( )
A.5 B.4 C.-5 D.-4
12.若|m|=5,|n|=7,m+n<0,则m﹣n的值是( )
A.﹣12或﹣2 B.﹣2或12 C.12或2 D.2或﹣12
二、填空题
13.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说______.
14.如图是某几何体的展开图,那么这个几何体是________.
15.将一个长方体截去一个角得到一个如图所示的新几何体,这个新几何体有_____个面.
16.比较大小: _____(填“>”“<”或“=”).
17.数轴上,点B在点A的右边,已知点A表示的数是﹣2,且AB=5.那么点B表示的数是_____.
18.在数轴上,点到原点的距离等于,点所表示的数是_________
三、解答题
19.如图,上面一行是一些具体的实物图形,下面一行是一些立体图形,试用线连接立体图形和类似的实物图形.
20.如图所示的几何体是由几个相形状同的正方体搭成的,请画出这个几何体的从正面、从左面、从上面看到的形状图.
几何体
从正面看
从左面看
从上面看
21.如图是由小正方形组成的图,请你用三种方法分别在下图中添画两个小正方形,使它能成为正方体的表面展开图.
22.把下列各数填在相应的大括号里.
+2019,-3.14,-4,-,6%,0,32
(1)正整数:{ }
(2)整数:{ }
(3)正分数:{ }
(4)负分数:{ }
23.计算:
(1)(﹣25)+(﹣35); (2)(﹣12)+(+3);
(3)(+8)+(﹣7); (4)0+(﹣7).
(5); (6);
(7); (8) .
24.在数轴上表示下列各数,并用“>”连接起来.
3,-4,,0,-1,1.
25.(1)计算: (2);
26.已知,.
(1)直接写出a、b的值;
(2)若a、b异号,求a-b的值.
27.检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A地出发,到收工时,行走记录为(单位:千米):+8,﹣9,+4,+7,﹣2,﹣10,+18,﹣3,+7,+4.回答下列问题:
(1)收工地点在A地的哪个方向?距A地多少千米?
(2)若每千米耗油0.3升,那么从A地出发到收工地点,共耗油多少升?
参考答案
1.B
【分析】
根据几何体的特征进行判断即可.
【详解】
A选项为圆柱,B选项为长方体,C选项为圆锥,D选项为四棱锥.
故选:B.
【点睛】
考查立体图形的认识,掌握立体图形的特征是解题的关键.
2.B
【分析】
依据正方体的展开图的基本类型可对A、C、D选项作出判断;
依据正方体的展开图中不能出现“凹”和“田”字型可对选项B作出判断.
【详解】
根据正方体表面展开图的特点可知:
A选项图属于“1—4—1”型,是正方体展开图;
B选项图属于“凹”字型,不是正方体的展开图;
C选项图属于“3—3”型,是正方体展开图;
D选项图属于“2—2—2”型,是正方体展开图.
故选B.
【点睛】
本题主要考查的是几何体的展开图,掌握正方体的展开图的特点是解题的关键.
3.C
【分析】
从上面看得到从左往右3列,正方形的个数依次为1,1,2,依此判别出图形即可.
【详解】
从上面看有三列,第一列是1个正方体,中间一列是1个正方体,第三列是2个正方体,
故选:C.
【点睛】
本题主要考查了简单几何体的三视图,关键是掌握三视图的定义,从上面看它得到的平面图形是俯视图.
4.B
【分析】
一个负数的绝对值是它的相反数,据此解题.
【详解】
故选:B.
【点睛】
本题考查绝对值的化简,是基础考点,难度容易,掌握绝对值的代数意义、绝对值的几何意义是解题关键.
5.D
【分析】
根据题意列出算式,再结合正负数的意义解答即可.
【详解】
解:因为规定向北为正,米,
所以他实际上向南走了5米.
故选:D.
【点睛】
本题考查了正负数和有理数加法在实际中的应用,属于常见题型,正确理解题意、熟练掌握基本知识是解题的关键.
6.B
【解析】
考点:数轴.
专题:阅读型.
分析:根据数轴上表示的数左减右加的原则计算即可.
解答:
∵数轴上的点M对应的数是-2,
∴将点M向右移动4个单位长度,此时点M表示的数是-2+4=2.故选B.
点评:本题考查的是数轴的定义及数轴上两点之间的距离公式,属较简单题目.
7.D
【分析】
正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此截面的形状可能是:三角形、四边形、五边形、六边形.根据此判断即可.
【详解】
用平面去截正方体时最多与六个面相交得六边形,因此截面的形状可能是:三角形、四边形、五边形、六边形,不可能是七边形.
故选D.
【点睛】
本题考查的是几何体的截面,解答本题的关键是认识几何体的截面只是几何体的其中一个方面的体现,同一个几何体可能会有不同的截面,不同的几何体也可能会有相同的截面.
8.B
【分析】
根据有理数的加减运算,可得温度范围,根据温度范围,可得答案.
【详解】
解:?18?2=?20℃,?18+2=?16℃,
温度范围:?20℃至?16℃,
A、?20℃<?17℃<?16℃,故A适合储藏此种水饺;
B、?22℃<?20℃,故B不适合储藏此种水饺;
C、?20℃<?18℃<?16℃,故C适合储藏此种水饺;
D、?20℃<?19℃<?16℃,故D适合储藏此种水饺;
故选:B.
【点睛】
本题考查了正数和负数,有理数的加法运算是解题关键,先算出适合温度的范围,再选出不适合的温度.
9.D
【分析】
依据题意列出算式,然后根据减法法则计算即可.
【详解】
℃.
故选:D.
【点睛】
本题主要考查了有理数的减法在实际生活中的应用,掌握有理数的减法法则是解题的关键.
10.B
【分析】
最小的正整数是1,最大的负整数是-1,绝对值最小的有理数是0,根据代数式计算即可.
【详解】
由题意得:a=1,b=-1,c=0,
则a + b + c=1+(-1)+0=0,
故选B.
【点睛】
此题考查了有理数的加减,此题的关键是知道最大的正整数是1,最大的负整数是-1,绝对值最小的有理数是0.
11.D
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,可得到b值,再利用正方体及其表面展开图的特点求出a,然后代入代数式进行计算即可.
【详解】
解:这是一个正方体的平面展开图,共有六个面,其中面“a”与面“1”相对,面“b”与面“3”相对,“2”与面“-2”相对.
因为相对面上两个数都互为相反数,
所以a=-1,b=-3,
故a+b=-4,选D.
【点睛】
注意正方体的空间图形,从相对面入手,分析及解答问题.
12.C
【分析】
根据题意,利用绝对值的意义求出m与n的值,再代入所求式子计算即可.
【详解】
解:∵|m|=5,|n|=7,且m+n<0,
∴m=5,n=﹣7;m=﹣5,n=﹣7,
可得m﹣n=12或2,
则m﹣n的值是12或2.
故选:C.
【点睛】
本题考查了绝对值的意义,掌握绝对值的意义求值是关键.
13.线动成面
【分析】
利用雨刷可看成线,扇面是面,即可求出答案.
【详解】
汽车的雨刷在挡风玻璃上画出一个扇面,这说明线动成面的数学原理.
故答案为:线动成面.
【点睛】
本题考查了点,线,面、体,此题较简单,解题时要灵活应用点、线、面、体之间的关系.
14.圆柱
【解析】
∵展开图中是由两个圆和一个矩形组成的,
∴该展开图对应的几何体是圆柱.
故答案是“圆柱”.
15.7
【分析】
观察图形可知,新几何体与原长方体比较,增加一个面,由此即可作答.
【详解】
解:长方体截去一角变成一个如图的新几何体,这个新几何体有7个面.
故答案为:7.
【点睛】
本题考查了截一个几何体.能比较新几何体与原长方体,得出面数的变化情况是解题关键.
16.<
【分析】
根据正数大于0,0大于负数,正数大于负数,可解答.
【详解】
∵-5是负数,3是正数;
∴-5<3;
故答案为:<.
【点睛】
本题考查了有理数大小的比较,牢记正数大于0,0大于负数,正数大于负数.
17.3.
【分析】
根据数轴表示数的意义,在点A的右边,到点A距离为5的点所表示的数为3.
【详解】
解:﹣2+5=3,
故答案为:3.
【点睛】
本题考查数轴表示数的意义和方法,在数轴表示的数右边总比左边的大.
18.3或-3
【分析】
与原点距离为3的点有两个,分别在原点的左边和右边,左边用减法,右边用加法计算即可.
【详解】
解:当点A在原点左边时,为0-3=-3;
当点A在原点右边时为3-0=3.
故答案为:3或-3.
【点睛】
本题主要考查了数的绝对值的几何意义.注意:在数轴上与一个点的距离为a的数有2个,在该点的左边和右边各一个.
19.解:如图所示.
【解析】
分析:上面第一个物体是一个足球,由一个完整的曲面组成,应与下面第四个图形球体连接;
上面第二个物体是一个柱体,由两个圆和一个曲面组成,应与下面第三个图形圆柱连接;
上面第三个物体类似椎体,由一个曲面和一个圆组成,应与下面第二个图形圆锥连接;
上面第四个物体是金字塔,由四个三角形组成,应与下面第五个图形三棱锥连接;
上面第五个物体由六个面组成,每个面都是正方形,应与下面第一个图形正方体连接.
详解:如图所示.
点睛:本题考查了认识立体图形,熟练掌握常见几何体的形状与实际问题的关系是解题的关键.
20.见解析
【分析】
根据题意画出不同角度的图形即可.
【详解】
如图所示:
几何体
从正面看
从左面看
从上面看
【点睛】
21.
【分析】
按照正方体及其表面展开图的特点分析作出图形即可.
【详解】
正方体有11种展开图,如下
??
根据正方体的11种展开图,题中的图可用如下三种方法方法作出:
故答案为
【点睛】
本题考查正方体的表面展开图,解题的关键是熟练掌握正方体的11种展开图.
22.(1)+2019,32;(2)+2019,-4,0,32;(3)6%;(4)-3.14,-.
【分析】
根据有理数分类解答即可。
【详解】
(1)正整数:+2019,32
(2)整数:+2019,-4,0,32
(3)正分数:6%
(4)负分数:-3.14,-.
【点睛】
关键在于掌握有理数的分类,特别是0的处理,0是整数,但既不是正数也不是负数.
23.(1)-60;(2)-9;(3)1;(4)-7;(5)-12;(6)8.8;(7);(8)3.2
【分析】
(1)原式利用同号两数相加的法则计算即可得到结果;
(2)原式利用异号两数相加的法则计算即可得到结果;
(3)原式利用异号两数相加的法则计算即可得到结果;
(4)原式利用0与任何数相加得这个数即可得到结果;
(5)原式利用减法法则计算即可得到结果;
(6)原式利用减法法则计算即可得到结果;
(7)原式利用减法法则计算即可得到结果;
(8)原式利用减法法则计算即可得到结果.
【详解】
(1)(﹣25)+(﹣35)=﹣(25+35)=﹣60;
(2)(﹣12)+(+3)=﹣(12﹣3)=﹣9;
(3)(+8)+(﹣7)=+(8﹣7)=1;
(4)0+(﹣7)=﹣7;
(5);
(6);
(7)=;
(8)=3.2.
【点睛】
本题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.
24.见解析,3>1>0>-1>-2>-4
【分析】
先在数轴上表示各个数,再比较即可.
【详解】
解:在数轴上表示如图示,
3>1>0>-1>-2>-4,
【点睛】
本题考查的是在数轴上表示有理数,利用数轴判断有理数的大小.
25.(1)-5;(2)1
【分析】
(1)根据有理数的加减运算法则计算即可;
(2)根据有理数的加减运算法则计算即可.
【详解】
(1)
;
(2)
.
【点睛】
本题主要考查了有理数的加减混合运算,熟记有理数的加减法法则是解答本题的关键.
26.(1),;(2)14或-14.
【分析】
(1)根据绝对值的意义直接写出即可;
(2)先由(1)题确定a、b异号时的值,再代入计算即可.
【详解】
解:(1),;
(2)因为a、b异号,所以当a=8时,b=-6,此时;当a=-8时,b=6,此时;
所以a-b=14或-14.
【点睛】
本题考查了绝对值的意义和有理数的减法,属于基础题型,解答(2)题时需要分类讨论.
27.(1)收工时在A地的东边,距A地24千米;(2)21.6升.
【分析】
(1)向东为正,向西为负,将行走记录相加,如果是正数,检修小组在A地东边;如果是负数,检修小组在A地西边;
(2)将每次记录的绝对值相加计算出总路程,然后乘以每千米耗油量即可.
【详解】
解:(1)+8﹣9+4+7﹣2﹣10+18﹣3+7+4=24,
∴收工地点在A地的东边,距A地24千米;
(2)|+8|+|﹣9|+|+4|+|+7|+|﹣2|+|﹣10|+|+18|+|﹣3|+|+7|+|+4|=72(千米),
72×0.3=21.6(升),
答:若每千米耗油0.3升,从A地出发到收工时,共耗油21.6升.
【点睛】
本题考查了有理数加法的实际应用以及正数和负数在实际生活中的应用,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
同课章节目录
