山东省济南市商河县教育东部联盟2020-2021学年七年级上学期期中数学试题(Word版含解析)
文档属性
| 名称 | 山东省济南市商河县教育东部联盟2020-2021学年七年级上学期期中数学试题(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 376.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览




文档简介
山东省济南市商河县2020-2021学年七年级上学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.-2019的相反数是( )
A.2019 B.-2019 C. D.
2.如果收入25元记作+25元,那么支出20元记作( )元
A.+5 B.+20 C.-5 D.-20
3.数字177.6用科学记数法表示为
A.0.1776×103 B.1.776×102 C.1.776×103 D.17.76×102
4.如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
A.遇 B.见 C.未 D.来
5.下列各组数中,结果相等的是( )
A.与 B. 与 C.与 D.与
6.下列运算正确的是( )
A. B.
C. D.
7.在一,-│-12│,(-1) 3,0,-(一5)中,负整数的个数有( )
A.1个 B.2个 C.3个 D.4个
8.下面说法正确的是( )
A.的倒数是 B.0是最小的非负数
C.是单项式 D.单项式的系数和次数为和4
9.一个两位数的个位数字是,十位数字是,那么这个两位数可以表示为( )
A. B. C. D.
10.在数轴上表示a,b两数的点如图,则下列判断正确的是( )
A.ab>0 B.
C.a+b>0 D.a-b>0
11.如果2xa+4y与3x2yb-2是同类项,那么ab的值是( )
A.6 B.-6 C.8 D.-8
12.如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第个图形中共有4005个三角形,则的值是( )
A.1002 B.1001 C.1000 D.999
二、填空题
13.用代数式表示:a的2倍与b的平方的差是______.
14.多项式ab2-5ab+2b-1的次数是______,常数项是______.
15.比较两数的大小: _____(填“<”,“>”,“=”)
16.对于任意有理数a、b,定义一种新运算“”,规则如下:ab=ab+a-b,例如:32=3×2+3-2,则(-2) 3=_________;
17.一个两位数,十位数字是,个位数字比十位数字的2倍少3,请用含的代数式表示这个两位数为______.(提示:代数式必须化简)
18.如图所示的运算程序中,若开始输入的x值为12,我们发现第1次输出的结果为6,第2次输出的结果为3,……,第2019次输出的结果为_________;
三、解答题
19.计算:(1)1-(-)2 (2)
20.计算:(1) (2)-33÷(-3)2-3×(-2)
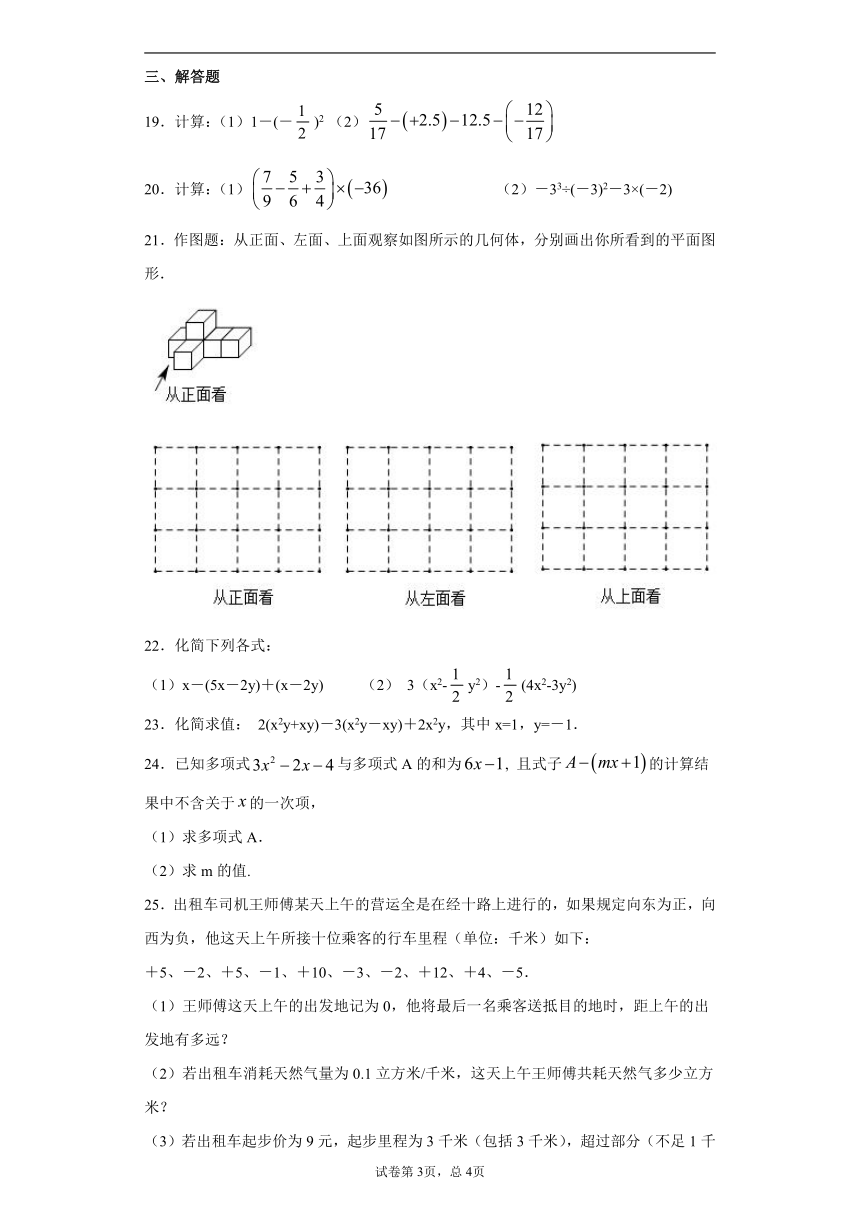
21.作图题:从正面、左面、上面观察如图所示的几何体,分别画出你所看到的平面图形.
22.化简下列各式:
(1)x-(5x-2y)+(x-2y) (2) 3(x2-y2)-(4x2-3y2)
23.化简求值: 2(x2y+xy)-3(x2y-xy)+2x2y,其中x=1,y=-1.
24.已知多项式与多项式A的和为, 且式子的计算结果中不含关于的一次项,
(1)求多项式A.
(2)求m的值.
25.出租车司机王师傅某天上午的营运全是在经十路上进行的,如果规定向东为正,向西为负,他这天上午所接十位乘客的行车里程(单位:千米)如下:
+5、-2、+5、-1、+10、-3、-2、+12、+4、-5.
(1)王师傅这天上午的出发地记为0,他将最后一名乘客送抵目的地时,距上午的出发地有多远?
(2)若出租车消耗天然气量为0.1立方米/千米,这天上午王师傅共耗天然气多少立方米?
(3)若出租车起步价为9元,起步里程为3千米(包括3千米),超过部分(不足1千米按1千米计算)每千米1.5元,这天上午王师傅共得车费多少元?
26.为了提高业主的宜居环境,在某居民区的建设中,因地制宜规划修建一个广场(图中阴影部分).
(1)用含、的代数式表示该广场的周长;
(2)用含、的代数式表示该广场的面积;
(3)当,时,求出该广场的周长和面积.
27.已知是最大的负整数,是的倒数,比小1,且、、分别是点、、在数轴上对应的数.若动点从点出发沿数轴正方向运动,动点同时从点出发沿数轴负方向运动,点的速度是每秒3个单位长度,点的速度是每秒1个单位长度.
(1)在数轴上标出点、、的位置;
(2)运动前、两点之间的距离为 ;运动t秒后,点,点运动的路程分别为 和 ;
(3)求运动几秒后,点与点相遇?
(4)在数轴上找一点,使点到、、三点的距离之和等于11,直接写出所有点对应的数.
参考答案
1.A
【分析】
根据只有符号不同的两个数是互为相反数解答即可.
【详解】
解:-2019的相反数是2019.
故选A.
【点睛】
本题考查了相反数的定义,解答本题的关键是熟练掌握相反数的定义,正数的相反数是负数,0的相反数是0,负数的相反数是正数.
2.D
【分析】
根据正数和负数表示相反意义的量,收入25元记作+25元,可得支出的表示方法.
【详解】
收入25元记作+25元,那么支出20元记作-20元,
故选D.
【点睛】
本题考查了正数和负数,收入记为正,支出记为负.
3.B
【分析】
用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.
【详解】
解:177.6=1.776×102.
故选B.
【点睛】
此题考查科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.
4.D
【解析】
试题分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,由此可得“遇”与“的”是相对面,“见”与“未”是相对面,“你”与“来”是相对面.故答案选D.
考点:正方体的展开图.
5.D
【分析】
本题涉及负数和分数的乘方,有括号与没有括号底数不相同,对各选项计算后即可选取答案.
【详解】
解:A、-12=-1,(-1)2=1,故本选项错误;
B、,,故本选项错误;
C、-|-2|=-2,-(-2)=2,故本选项错误;
D、(-3)3=-27,-33=-27,故本选项正确.
故选:D.
【点睛】
本题主要考查有理数的乘方运算,属于基础知识.
6.C
【分析】
根据同类项的定义以及合并同类项法则逐个选项计算即可解答.
【详解】
A.不是同类项,不能合并,故A选项错误;
B.不是同类项,不能合并,故B选项错误;
C. ,正确;
D. ,故D选项错误;
故选C.
【点睛】
本题考查同类项的识别以及合并同类项,熟练掌握以上知识点是解题关键.
7.B
【分析】
正整数,0,负整数组成整数,审清题意本题要选的是负整数.
【详解】
以上数据中只有-│-12│,(-1) 3,是负整数.
故选B.
【点睛】
此题考查负整数的概念,解题关键在于掌握其定义.
8.B
【分析】
根据倒数的概念、有理数的分类以及单项式的系数和次数定义,逐个选项判断即可解答.
【详解】
A. 的倒数是,故A选项错误;
B. 0是最小的非负数,故B选项正确;
C. 不是整式,故C选项错误;
D. 单项式的系数和次数为和3,故D选项错误;
故选B
【点睛】
本题考查倒数、有理数分类、单项式的识别以及单项式的系数和次数,熟练掌握倒数的概念、有理数的分类以及单项式的系数和次数定义是解题关键.
9.A
【分析】
依据两位数=10×十位数字+个位数字即可解答.
【详解】
这个两位数可表示为:10b+a.
故选:A.
【点睛】
此题考查列代数式—用代数式表示几位数.用“计数单位表示的数乘以该数位上的数字再把它们相加”即可列出代数式表示几位数.
10.D
【分析】
根据数轴可知,a>0,b<0且b的绝对值大于a的绝对值,再根据有理数的运算法则判断即可.
【详解】
解:∵a>0,b<0,
∴ab<0,a+b<0,a-b>0,
故选:D.
【点睛】
本题考查有理数的运算法则和绝对值的意义,结合数轴判断a.b符号和绝对值大小是解题的关键.
11.D
【分析】
先根据同类项的定义可得a、b的值,再代入计算有理数的乘方即可得.
【详解】
由同类项的定义得:,解得,
则,
故选:D.
【点睛】
本题考查了同类项、有理数的乘方,熟记同类项的定义是解题关键.
12.A
【分析】
观察图形,可知第1个图形,有1个三角形;第2个图形,有5个三角形;第3个图形,有9个三角形;……找出规律,第n个图形,有4n-3个三角形;列出方程,求解即可.
【详解】
第1个图形,有1个三角形;1=1×4-3
第2个图形,有5个三角形;5=2×4-3
第3个图形,有9个三角形;9=3×4-3
……
第n个图形,有(4n-3)个三角形;
所以,4n-3=4005
解得:n=1002
故选A
【点睛】
本题考查用代数式表示图形的变化规律,正确总结和归纳是解题关键.
13.4a2-b2.
【分析】
本题考查列代数式,要明确给出文字语言中的运算关系,先求倍数,然后求差,再求平方.
【详解】
解:a的2倍为2a,与b的平方差为(2a)2-b2=4a2-b2, 故答案为4a2-b2.
【点睛】
本题主要考查了列代数式的知识,解决本题的关键是要正确理解文字语言中的关键词.
14.3
【分析】
根据多项式的次数、常数项的定义即可得.
【详解】
多项式的次数是,常数项是,
故答案为:3,.
【点睛】
本题考查了多项式的次数和常数项,熟记定义是解题关键.
15.>
【解析】
先通分可得=,=,根据两负数相比较,绝对值大的反而小,可知>.
故答案为>.
点睛:此题主要考查了有理数的大小比较,解题时,根据有理数的大小比较的方法,负数小于0,正数大于0,两负数相比较,绝对值大的反而小,进行比较即可,解题关键是先要通分,然后比较其绝对值.
16.-11.
【分析】
根据a⊕b=ab+a-b,可以求得题目中所求式子的值,本题得以解决.
【详解】
∵a⊕b=ab+a-b,
∴(-4)⊕5
=(-2)×3+(-2)-3
=(-6)+(-5)
=-11,
故答案为-11.
【点睛】
此题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
17.
【分析】
根据题意表示出个位数字,再根据两位数字表示方式:十位数字×10+个位数字,表示出这个两位数,再化简即可.
【详解】
一个两位数,十位数字是,个位数字比十位数字的2倍少3,
那么这个数字的个位数字是:,
两位数字表示方式:十位数字×10+个位数字
这个两位数为:
故答案为
【点睛】
本题考查列代数式以及用代数式表示数字,熟练掌握该知识点是解题关键.
18.8.
【分析】
把x=12代入运算程序中计算,以此类推得到第2015次输出的结果即可.
【详解】
把x=12代入得:×12=6,
把x=6代入得:×6=3,
把x=3代入得:3+5=8,
把x=8代入得:×8=4,
把x=4代入得:×4=2,
把x=2代入得:×2=1,
把x=1代入得:1+5=6,
以此类推,以6,3,8,4,2,1循环,
∵2019÷6=336…3,
∴2017次输出的结果为8,
故答案为8.
【点睛】
此题考查代数式求值,弄清题中的运算程序是解本题的关键.
19.(1);(2).
【分析】
(1)先计算有理数的乘方,再计算有理数的减法即可得;
(2)先去括号,再利用有理数加减法的交换律与结合律进行计算即可得.
【详解】
(1)原式,
;
(2)原式,
,
,
.
【点睛】
本题考查了含乘方的有理数混合运算、有理数加减法的交换律与结合律,熟练掌握各运算法则和运算律是解题关键.
20.(1)-25;(2) 3
【分析】
(1)根据乘法分配律可以解答本题;
(2)根据有理数的乘方、有理数的乘除法和减法可以解答本题.
【详解】
解:(1)
,
(2)
=
=3
【点睛】
本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
21.见解析.
【分析】
直接利用画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等,进而得出答案.
【详解】
【点睛】
此题主要考查了作三视图,正确把握观察角度进而得出三视图的形状是解题关键.
22.(1);(2).
【分析】
(1)先去括号,再计算整式的加减运算即可得;
(2)先去括号,再计算整式的加减运算即可得.
【详解】
(1)原式,
;
(2)原式,
.
【点睛】
本题考查了整式的加减运算,熟记运算法则是解题关键.
23.,.
【分析】
先去括号,再计算整式的加减运算,然后将x、y的值代入求值即可得.
【详解】
原式,
,
将代入得:原式.
【点睛】
本题考查了整式的化简求值,熟练掌握整式的加减运算法则是解题关键.
24.(1);(2)8
【分析】
(1)根据题意列出关系式,去括号合并得到最简结果即可得多项式A.
(2)由结果不含x的一次项求出m的值即可.
【详解】
(1)根据题意,得A=-()
=
=.
(2)=
=,
∵结果中不含关于的一次项,
∴,即.
【点睛】
本题考查了了整式的加减,熟练掌握运算法则是解题的关键.
25.(1)23千米;(2)4.9立方米;(3)124.5元.
【分析】
(1)根据正数和负数的实际意义,将所有数相加,然后根据结果回答;
(2)王师傅所行路程和为所有数的绝对值之和,王师傅所行路程和与0.1的乘积,就是这天上午王师傅共耗天然气数量;
(3)根据题意,分别计算出每位乘客的车费,再求和即可.
【详解】
解:(1)5-2+5-1+10-3-2+12+4-5=23(千米)
答:距上午的出发地23千米;
(2)0.1×(5+2+5+1+10+3+2+12+4+5)=0.1×49=4.9(立方米)
答:这天上午王师傅共耗天然气4.9立方米;
(3)第一个人的车费为:(元)
第二个人的车费为:(元)
第三个人的车费为:(元)
第四个人的车费为:(元)
第五个人的车费为:(元)
第六个人的车费为:(元)
第七个人的车费为:(元)
第八个人的车费为:(元)
第九个人的车费为:(元)
第十个人的车费为:(元)
这天上午王师傅共得车费为:12+9+12+9+19.5+9+9+22.5+10.5+12=124.5(元)
答:这天上午王师傅共得车费为124.5元.
【点睛】
本题考查正负数的实际应用以及有理数混合运算的实际应用,熟练掌握以上知识点是解题关键.
26.(1);(2);(3)68,168
【分析】
(1)根据图形,用代数式表示广场的周长即可;
(2)观察图形可知,广场的面积=大长方形的面积-中间空白长方形的面积,用代数式表示即可;
(3)将,代入(1)(2)所求代数式,求值即可.
【详解】
解:(1)广场的周长
(2)广场的面积
(3)当,时
广场的周长
广场的面积
【点睛】
本题考查用代数式表示几何图形的面积和周长以及代数式求值,熟练掌握列代数式和代数式求值是解题关键.
27.(1)见解析;(2)6;3t;t.;(3)运动1.5秒后,点与点相遇;(4)或
【分析】
(1)按照整数、倒数的概念,确定a、b、c的值,并在数轴上表示出来即可;
(2)观察数轴可知运动前、两点之间的距离为AB,再利用路程=速度×时间,即可用含t的代数式表示点,点运动的路程;
(3)点与点相遇,则点P运动路程与点Q运动路程的和为AB的长,列出方程,求解即可;
(4)分情况讨论:当点M在C点左侧时;当点M在A、C之间时;当点M在A、B之间时;当点M在B点右侧时;设点M表示的数是m,利用数轴上点之间的距离=大数减小数,列出方程求解,再根据情况取舍即可.
【详解】
(1)是最大的负整数,则a=-1
是的倒数,则b=5
比小1,则c=-1-1=-2
(2)运动前、两点之间的距离为AB=5-(-1)=6
点P运动路程为3t,点Q运动路程为t,
故答案为6;3t;t.
(3)点与点相遇,则点P运动路程与点Q运动路程的和为6
即:3t+t=6,
解得:t=1.5
故:运动1.5秒后,点与点相遇;
(4)设点M表示的数是m,
当点M在C点左侧时,MC+MA+MB=-2-m+(-1)-m+5-m=11
解得:,
所以,点对应的数为;
当点M在A、C之间时,MC+MA+MB=m-(-2)+(-1)-m+5-m=11
解得:(舍去);
当点M在A、B之间时,MC+MA+MB=m-(-2)+m-(-1)+5-m=11
解得:,
所以,点对应的数为
当点M在B点右侧时,MC+MA+MB= m-(-2)+m-(-1)+m-5=11
解得:(舍去),
所以点对应的数为或.
【点睛】
本题考查数轴、数轴上两点间的距离以及动点问题,熟练掌握求数轴上点的距离的公式是解题关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.-2019的相反数是( )
A.2019 B.-2019 C. D.
2.如果收入25元记作+25元,那么支出20元记作( )元
A.+5 B.+20 C.-5 D.-20
3.数字177.6用科学记数法表示为
A.0.1776×103 B.1.776×102 C.1.776×103 D.17.76×102
4.如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
A.遇 B.见 C.未 D.来
5.下列各组数中,结果相等的是( )
A.与 B. 与 C.与 D.与
6.下列运算正确的是( )
A. B.
C. D.
7.在一,-│-12│,(-1) 3,0,-(一5)中,负整数的个数有( )
A.1个 B.2个 C.3个 D.4个
8.下面说法正确的是( )
A.的倒数是 B.0是最小的非负数
C.是单项式 D.单项式的系数和次数为和4
9.一个两位数的个位数字是,十位数字是,那么这个两位数可以表示为( )
A. B. C. D.
10.在数轴上表示a,b两数的点如图,则下列判断正确的是( )
A.ab>0 B.
C.a+b>0 D.a-b>0
11.如果2xa+4y与3x2yb-2是同类项,那么ab的值是( )
A.6 B.-6 C.8 D.-8
12.如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第个图形中共有4005个三角形,则的值是( )
A.1002 B.1001 C.1000 D.999
二、填空题
13.用代数式表示:a的2倍与b的平方的差是______.
14.多项式ab2-5ab+2b-1的次数是______,常数项是______.
15.比较两数的大小: _____(填“<”,“>”,“=”)
16.对于任意有理数a、b,定义一种新运算“”,规则如下:ab=ab+a-b,例如:32=3×2+3-2,则(-2) 3=_________;
17.一个两位数,十位数字是,个位数字比十位数字的2倍少3,请用含的代数式表示这个两位数为______.(提示:代数式必须化简)
18.如图所示的运算程序中,若开始输入的x值为12,我们发现第1次输出的结果为6,第2次输出的结果为3,……,第2019次输出的结果为_________;
三、解答题
19.计算:(1)1-(-)2 (2)
20.计算:(1) (2)-33÷(-3)2-3×(-2)
21.作图题:从正面、左面、上面观察如图所示的几何体,分别画出你所看到的平面图形.
22.化简下列各式:
(1)x-(5x-2y)+(x-2y) (2) 3(x2-y2)-(4x2-3y2)
23.化简求值: 2(x2y+xy)-3(x2y-xy)+2x2y,其中x=1,y=-1.
24.已知多项式与多项式A的和为, 且式子的计算结果中不含关于的一次项,
(1)求多项式A.
(2)求m的值.
25.出租车司机王师傅某天上午的营运全是在经十路上进行的,如果规定向东为正,向西为负,他这天上午所接十位乘客的行车里程(单位:千米)如下:
+5、-2、+5、-1、+10、-3、-2、+12、+4、-5.
(1)王师傅这天上午的出发地记为0,他将最后一名乘客送抵目的地时,距上午的出发地有多远?
(2)若出租车消耗天然气量为0.1立方米/千米,这天上午王师傅共耗天然气多少立方米?
(3)若出租车起步价为9元,起步里程为3千米(包括3千米),超过部分(不足1千米按1千米计算)每千米1.5元,这天上午王师傅共得车费多少元?
26.为了提高业主的宜居环境,在某居民区的建设中,因地制宜规划修建一个广场(图中阴影部分).
(1)用含、的代数式表示该广场的周长;
(2)用含、的代数式表示该广场的面积;
(3)当,时,求出该广场的周长和面积.
27.已知是最大的负整数,是的倒数,比小1,且、、分别是点、、在数轴上对应的数.若动点从点出发沿数轴正方向运动,动点同时从点出发沿数轴负方向运动,点的速度是每秒3个单位长度,点的速度是每秒1个单位长度.
(1)在数轴上标出点、、的位置;
(2)运动前、两点之间的距离为 ;运动t秒后,点,点运动的路程分别为 和 ;
(3)求运动几秒后,点与点相遇?
(4)在数轴上找一点,使点到、、三点的距离之和等于11,直接写出所有点对应的数.
参考答案
1.A
【分析】
根据只有符号不同的两个数是互为相反数解答即可.
【详解】
解:-2019的相反数是2019.
故选A.
【点睛】
本题考查了相反数的定义,解答本题的关键是熟练掌握相反数的定义,正数的相反数是负数,0的相反数是0,负数的相反数是正数.
2.D
【分析】
根据正数和负数表示相反意义的量,收入25元记作+25元,可得支出的表示方法.
【详解】
收入25元记作+25元,那么支出20元记作-20元,
故选D.
【点睛】
本题考查了正数和负数,收入记为正,支出记为负.
3.B
【分析】
用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.
【详解】
解:177.6=1.776×102.
故选B.
【点睛】
此题考查科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.
4.D
【解析】
试题分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,由此可得“遇”与“的”是相对面,“见”与“未”是相对面,“你”与“来”是相对面.故答案选D.
考点:正方体的展开图.
5.D
【分析】
本题涉及负数和分数的乘方,有括号与没有括号底数不相同,对各选项计算后即可选取答案.
【详解】
解:A、-12=-1,(-1)2=1,故本选项错误;
B、,,故本选项错误;
C、-|-2|=-2,-(-2)=2,故本选项错误;
D、(-3)3=-27,-33=-27,故本选项正确.
故选:D.
【点睛】
本题主要考查有理数的乘方运算,属于基础知识.
6.C
【分析】
根据同类项的定义以及合并同类项法则逐个选项计算即可解答.
【详解】
A.不是同类项,不能合并,故A选项错误;
B.不是同类项,不能合并,故B选项错误;
C. ,正确;
D. ,故D选项错误;
故选C.
【点睛】
本题考查同类项的识别以及合并同类项,熟练掌握以上知识点是解题关键.
7.B
【分析】
正整数,0,负整数组成整数,审清题意本题要选的是负整数.
【详解】
以上数据中只有-│-12│,(-1) 3,是负整数.
故选B.
【点睛】
此题考查负整数的概念,解题关键在于掌握其定义.
8.B
【分析】
根据倒数的概念、有理数的分类以及单项式的系数和次数定义,逐个选项判断即可解答.
【详解】
A. 的倒数是,故A选项错误;
B. 0是最小的非负数,故B选项正确;
C. 不是整式,故C选项错误;
D. 单项式的系数和次数为和3,故D选项错误;
故选B
【点睛】
本题考查倒数、有理数分类、单项式的识别以及单项式的系数和次数,熟练掌握倒数的概念、有理数的分类以及单项式的系数和次数定义是解题关键.
9.A
【分析】
依据两位数=10×十位数字+个位数字即可解答.
【详解】
这个两位数可表示为:10b+a.
故选:A.
【点睛】
此题考查列代数式—用代数式表示几位数.用“计数单位表示的数乘以该数位上的数字再把它们相加”即可列出代数式表示几位数.
10.D
【分析】
根据数轴可知,a>0,b<0且b的绝对值大于a的绝对值,再根据有理数的运算法则判断即可.
【详解】
解:∵a>0,b<0,
∴ab<0,a+b<0,a-b>0,
故选:D.
【点睛】
本题考查有理数的运算法则和绝对值的意义,结合数轴判断a.b符号和绝对值大小是解题的关键.
11.D
【分析】
先根据同类项的定义可得a、b的值,再代入计算有理数的乘方即可得.
【详解】
由同类项的定义得:,解得,
则,
故选:D.
【点睛】
本题考查了同类项、有理数的乘方,熟记同类项的定义是解题关键.
12.A
【分析】
观察图形,可知第1个图形,有1个三角形;第2个图形,有5个三角形;第3个图形,有9个三角形;……找出规律,第n个图形,有4n-3个三角形;列出方程,求解即可.
【详解】
第1个图形,有1个三角形;1=1×4-3
第2个图形,有5个三角形;5=2×4-3
第3个图形,有9个三角形;9=3×4-3
……
第n个图形,有(4n-3)个三角形;
所以,4n-3=4005
解得:n=1002
故选A
【点睛】
本题考查用代数式表示图形的变化规律,正确总结和归纳是解题关键.
13.4a2-b2.
【分析】
本题考查列代数式,要明确给出文字语言中的运算关系,先求倍数,然后求差,再求平方.
【详解】
解:a的2倍为2a,与b的平方差为(2a)2-b2=4a2-b2, 故答案为4a2-b2.
【点睛】
本题主要考查了列代数式的知识,解决本题的关键是要正确理解文字语言中的关键词.
14.3
【分析】
根据多项式的次数、常数项的定义即可得.
【详解】
多项式的次数是,常数项是,
故答案为:3,.
【点睛】
本题考查了多项式的次数和常数项,熟记定义是解题关键.
15.>
【解析】
先通分可得=,=,根据两负数相比较,绝对值大的反而小,可知>.
故答案为>.
点睛:此题主要考查了有理数的大小比较,解题时,根据有理数的大小比较的方法,负数小于0,正数大于0,两负数相比较,绝对值大的反而小,进行比较即可,解题关键是先要通分,然后比较其绝对值.
16.-11.
【分析】
根据a⊕b=ab+a-b,可以求得题目中所求式子的值,本题得以解决.
【详解】
∵a⊕b=ab+a-b,
∴(-4)⊕5
=(-2)×3+(-2)-3
=(-6)+(-5)
=-11,
故答案为-11.
【点睛】
此题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
17.
【分析】
根据题意表示出个位数字,再根据两位数字表示方式:十位数字×10+个位数字,表示出这个两位数,再化简即可.
【详解】
一个两位数,十位数字是,个位数字比十位数字的2倍少3,
那么这个数字的个位数字是:,
两位数字表示方式:十位数字×10+个位数字
这个两位数为:
故答案为
【点睛】
本题考查列代数式以及用代数式表示数字,熟练掌握该知识点是解题关键.
18.8.
【分析】
把x=12代入运算程序中计算,以此类推得到第2015次输出的结果即可.
【详解】
把x=12代入得:×12=6,
把x=6代入得:×6=3,
把x=3代入得:3+5=8,
把x=8代入得:×8=4,
把x=4代入得:×4=2,
把x=2代入得:×2=1,
把x=1代入得:1+5=6,
以此类推,以6,3,8,4,2,1循环,
∵2019÷6=336…3,
∴2017次输出的结果为8,
故答案为8.
【点睛】
此题考查代数式求值,弄清题中的运算程序是解本题的关键.
19.(1);(2).
【分析】
(1)先计算有理数的乘方,再计算有理数的减法即可得;
(2)先去括号,再利用有理数加减法的交换律与结合律进行计算即可得.
【详解】
(1)原式,
;
(2)原式,
,
,
.
【点睛】
本题考查了含乘方的有理数混合运算、有理数加减法的交换律与结合律,熟练掌握各运算法则和运算律是解题关键.
20.(1)-25;(2) 3
【分析】
(1)根据乘法分配律可以解答本题;
(2)根据有理数的乘方、有理数的乘除法和减法可以解答本题.
【详解】
解:(1)
,
(2)
=
=3
【点睛】
本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
21.见解析.
【分析】
直接利用画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等,进而得出答案.
【详解】
【点睛】
此题主要考查了作三视图,正确把握观察角度进而得出三视图的形状是解题关键.
22.(1);(2).
【分析】
(1)先去括号,再计算整式的加减运算即可得;
(2)先去括号,再计算整式的加减运算即可得.
【详解】
(1)原式,
;
(2)原式,
.
【点睛】
本题考查了整式的加减运算,熟记运算法则是解题关键.
23.,.
【分析】
先去括号,再计算整式的加减运算,然后将x、y的值代入求值即可得.
【详解】
原式,
,
将代入得:原式.
【点睛】
本题考查了整式的化简求值,熟练掌握整式的加减运算法则是解题关键.
24.(1);(2)8
【分析】
(1)根据题意列出关系式,去括号合并得到最简结果即可得多项式A.
(2)由结果不含x的一次项求出m的值即可.
【详解】
(1)根据题意,得A=-()
=
=.
(2)=
=,
∵结果中不含关于的一次项,
∴,即.
【点睛】
本题考查了了整式的加减,熟练掌握运算法则是解题的关键.
25.(1)23千米;(2)4.9立方米;(3)124.5元.
【分析】
(1)根据正数和负数的实际意义,将所有数相加,然后根据结果回答;
(2)王师傅所行路程和为所有数的绝对值之和,王师傅所行路程和与0.1的乘积,就是这天上午王师傅共耗天然气数量;
(3)根据题意,分别计算出每位乘客的车费,再求和即可.
【详解】
解:(1)5-2+5-1+10-3-2+12+4-5=23(千米)
答:距上午的出发地23千米;
(2)0.1×(5+2+5+1+10+3+2+12+4+5)=0.1×49=4.9(立方米)
答:这天上午王师傅共耗天然气4.9立方米;
(3)第一个人的车费为:(元)
第二个人的车费为:(元)
第三个人的车费为:(元)
第四个人的车费为:(元)
第五个人的车费为:(元)
第六个人的车费为:(元)
第七个人的车费为:(元)
第八个人的车费为:(元)
第九个人的车费为:(元)
第十个人的车费为:(元)
这天上午王师傅共得车费为:12+9+12+9+19.5+9+9+22.5+10.5+12=124.5(元)
答:这天上午王师傅共得车费为124.5元.
【点睛】
本题考查正负数的实际应用以及有理数混合运算的实际应用,熟练掌握以上知识点是解题关键.
26.(1);(2);(3)68,168
【分析】
(1)根据图形,用代数式表示广场的周长即可;
(2)观察图形可知,广场的面积=大长方形的面积-中间空白长方形的面积,用代数式表示即可;
(3)将,代入(1)(2)所求代数式,求值即可.
【详解】
解:(1)广场的周长
(2)广场的面积
(3)当,时
广场的周长
广场的面积
【点睛】
本题考查用代数式表示几何图形的面积和周长以及代数式求值,熟练掌握列代数式和代数式求值是解题关键.
27.(1)见解析;(2)6;3t;t.;(3)运动1.5秒后,点与点相遇;(4)或
【分析】
(1)按照整数、倒数的概念,确定a、b、c的值,并在数轴上表示出来即可;
(2)观察数轴可知运动前、两点之间的距离为AB,再利用路程=速度×时间,即可用含t的代数式表示点,点运动的路程;
(3)点与点相遇,则点P运动路程与点Q运动路程的和为AB的长,列出方程,求解即可;
(4)分情况讨论:当点M在C点左侧时;当点M在A、C之间时;当点M在A、B之间时;当点M在B点右侧时;设点M表示的数是m,利用数轴上点之间的距离=大数减小数,列出方程求解,再根据情况取舍即可.
【详解】
(1)是最大的负整数,则a=-1
是的倒数,则b=5
比小1,则c=-1-1=-2
(2)运动前、两点之间的距离为AB=5-(-1)=6
点P运动路程为3t,点Q运动路程为t,
故答案为6;3t;t.
(3)点与点相遇,则点P运动路程与点Q运动路程的和为6
即:3t+t=6,
解得:t=1.5
故:运动1.5秒后,点与点相遇;
(4)设点M表示的数是m,
当点M在C点左侧时,MC+MA+MB=-2-m+(-1)-m+5-m=11
解得:,
所以,点对应的数为;
当点M在A、C之间时,MC+MA+MB=m-(-2)+(-1)-m+5-m=11
解得:(舍去);
当点M在A、B之间时,MC+MA+MB=m-(-2)+m-(-1)+5-m=11
解得:,
所以,点对应的数为
当点M在B点右侧时,MC+MA+MB= m-(-2)+m-(-1)+m-5=11
解得:(舍去),
所以点对应的数为或.
【点睛】
本题考查数轴、数轴上两点间的距离以及动点问题,熟练掌握求数轴上点的距离的公式是解题关键.
同课章节目录
