山东省临沂市沂南县2020--2021学年七年级上学期期中数学试题(Word版 含解析)
文档属性
| 名称 | 山东省临沂市沂南县2020--2021学年七年级上学期期中数学试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 461.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 14:01:02 | ||
图片预览




文档简介
山东省临沂市沂南县2020--2021学年七年级上学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.的相反数是( )
A. B.2020 C. D.
2.下列各数种,比小的数是( )
A. B. C.0 D.3
3.用四舍五入法对1.8935取近似值,若精确到0.001,则下列各数种,正确的是( )
A.1.890 B.1.893 C.1.894 D.1.89
4.天气预报,某月5日的气温是-3℃~5℃.则这天的温差(最高气温减最低气温,单位:℃)是( )
A.8 B.2 C. D.
5.数轴上,点A表示的数是1,点与点距离2个单位长度,则点表示的数是( )
A.3 B. C.2 D.3或
6.下列不是同类项的是( )
A.和 B.和
C.和 D.和
7.下列各组有理数的大小比较中,正确的是( )
A. B.
C. D.
8.下列各式中,去括号正确的是( )
A. B.
C. D.
9.下列各式的计算,正确的是( )
A. B.
C. D.
10.若单项式与的和仍为单项式,则的值是( )
A.1 B.-1 C.5 D.-5
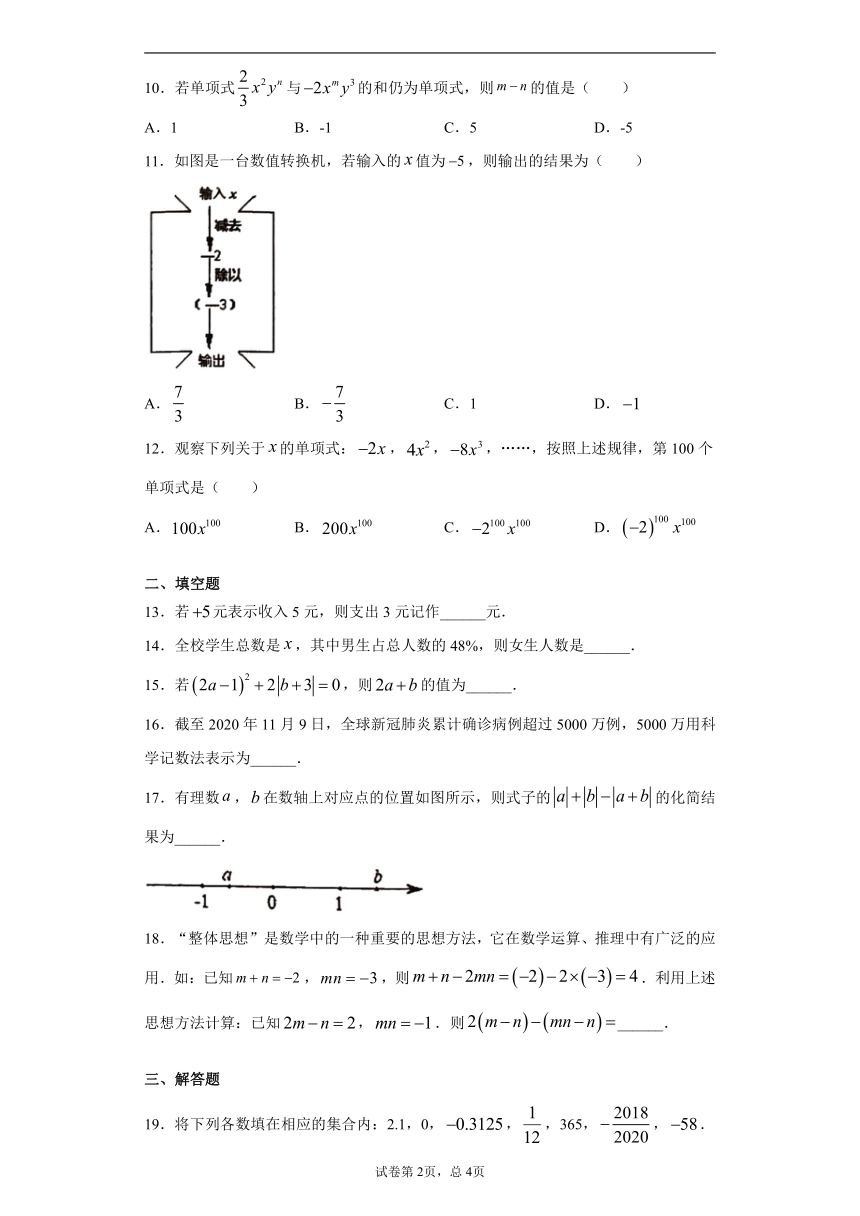
11.如图是一台数值转换机,若输入的值为,则输出的结果为( )
A. B. C.1 D.
12.观察下列关于的单项式:,,,……,按照上述规律,第100个单项式是( )
A. B. C. D.
二、填空题
13.若元表示收入5元,则支出3元记作______元.
14.全校学生总数是,其中男生占总人数的48%,则女生人数是______.
15.若,则的值为______.
16.截至2020年11月9日,全球新冠肺炎累计确诊病例超过5000万例,5000万用科学记数法表示为______.
17.有理数,在数轴上对应点的位置如图所示,则式子的的化简结果为______.
18.“整体思想”是数学中的一种重要的思想方法,它在数学运算、推理中有广泛的应用.如:已知,,则.利用上述思想方法计算:已知,.则______.
三、解答题
19.将下列各数填在相应的集合内:2.1,0,,,365,,.
整数集合:;
负数集合:;
负分数集合:;
非负数集合:.
20.计算:
(1); (2).
21.如图是一条不完整的数轴,请你补充完整,并在数轴上标出下列各数,然后把这些数用“<”连接起来:,,.
22.先化简,再求值:,其中,.
23.在互联网技术的影响下,幸福新村的村民小刘在网上销售苹果,原计划每天卖100千克,但实际每天的销量与计划销量相比有出入,如表是某周的销售情况(超额记为正,不足记为负.单位:千克):
星期
一
二
三
四
五
六
日
与计划量的差值
(1)根据表中的数据可知前三天共卖出___________千克;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售多少千克?
(3)若每千克按5元出售,每千克苹果的运费为1元,那么小刘本周一共收入多少元?
24.甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同,甲商场规定:凡超过元的电器,超出的金额按收取;乙商场规定:凡超过元的电器,超出的金额按收取,某顾客购买的电器价格是元.
(1)当时,分别用代数式表示在两家商场购买电器所需付的费用
(2)当时,该顾客应选择哪一家商场购买比较合算?说明理由.
25.如图所示,在数轴上点,,表示的数分别为,0,6.点与点之间的距离表示为,点与点之间的距离表示为,点与点之间的距离表示为.
(1)______,______,______;
(2)点,,开始在数轴上运动,若点以每秒1个单位长度的速度向左运动,同时点和点分别以每秒2个单位长度和5个单位长度的速度向右运动.
①设运动时间为,请用含有的算式分别表示出,,;
②在①的条件下,请问:的值是否随着运动时间的变化而变化?若变化,请说明理由;若不变,请求其值.
参考答案
1.B
【分析】
根据相反数的定义:只有符号不同的两个数互为相反数,即可得出结论.
【详解】
解:的相反数是:2020.
故选B.
【点睛】
此题考查的是求一个数的相反数,掌握相反数的定义是解题关键.
2.A
【分析】
先根据正数都大于0,负数都小于0,可排除C、D,再根据两个负数,绝对值大的反而小,即可得出结论.
【详解】
解:先根据正数都大于0,负数都小于0,可排除C、D,
∵=4,=3,,而4>3>2
∴<<
∴各选项中,比小的数是
故选A.
【点睛】
此题考查的是有理数的比较大小,掌握正数都大于0;负数都小于0;两个负数,绝对值大的反而小,是解题关键.
3.C
【分析】
把1.8935千分位上的5四舍五入即可.
【详解】
解:精确到0.001,1.8935≈1.894
故选C.
【点睛】
此题考查的是求一个数的近似数,掌握四舍五入法是解题关键.
4.A
【分析】
根据温差=最高气温-最低气温和有理数的减法法则计算即可.
【详解】
解:这天的温差为5-(-3)=8℃
故选A.
【点睛】
此题考查的是有理数减法的应用,掌握温差=最高气温-最低气温是解题关键.
5.D
【分析】
先根据点A和点B的位置分类讨论,再根据点A表示的数和A、B两点的距离分别求解即可.
【详解】
解:若点B在点A的左侧,
∵点A表示的数是1,点与点距离2个单位长度,
∴点B表示的数为1-2=-1;
若点B在点A的右侧,
∵点A表示的数是1,点与点距离2个单位长度,
∴点B表示的数为1+2=3;
综上:点B表示的数为3或
故选D.
【点睛】
此题考查的是根据数轴上两点的距离和一点所表示的数,求另一点所表示的数,掌握分类讨论是数学思想和数轴上两点之间的距离公式是解题关键.
6.C
【分析】
根据同类项的定义:如果两个单项式,它们所含的字母相同,并且相同字母的指数也分别相同,那么就称这两个单项式为同类项,逐一判断即可.
【详解】
解:A.或是同类项,故不符合题意;
B.和是同类项,故不符合题意;
C.和不是同类项,故符合题意;
D.和是同类项,故不符合题意.
故选C.
【点睛】
此题考查的是同类项的判断,掌握同类项的定义是解题关键.
7.C
【分析】
先将多重符号和绝对值化简,然后根据有理数的比较大小方法逐一判断即可.
【详解】
解:A.,而1>-2,所以,故错误;
B.,而-3<2,所以,故错误;
C.,而,所以,故正确;
D. ,而,所以,故错误.
故选C.
【点睛】
此题考查的是有理数的比较大小,解题关键是先将多重符号和绝对值化简.
8.C
【分析】
各式去括号得到结果,即可作出判断.
【详解】
解:,故A错误;
,故B,D错误,C正确.
故选:C.
【点睛】
此题考查了去括号与添括号,熟练掌握去括号法则是解本题的关键.
9.D
【分析】
根据同类项的定义和合并同类项法则逐一判断即可.
【详解】
解:A.,故本选项错误;
B.和不是同类项,不能合并,故错误;
C.和不是同类项,不能合并,故错误;
D.,故正确.
故选D.
【点睛】
此题考查的是同类项的判断和合并同类项,掌握同类项的定义和合并同类项法则是解题关键.
10.B
【详解】
∵单项式x2yn与-2xmy3的和仍为单项式,
∴它们是同类项,
∴m=2,n=3,
∴m-n=-1.
故选B.
【点睛】
同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同,从而得出m,n的值.
11.C
【分析】
根据数值转换机的运算规则计算即可.
【详解】
解:根据题意可得:[(-5)-(-2)]÷(-3)=(-3) ÷(-3)= 1.
故选C.
【点睛】
此题考查的是有理数的混合运算,掌握有理数的各个运算法则是解题关键.
12.D
【分析】
根据已知单项式的排列规律,推出第n个单项式,从而求出结论.
【详解】
解:∵=
=
=
∴第n个单项式为
∴第100个单项式是
故选D.
【点睛】
此题考查的是探索规律题,找出规律并归纳公式是解题关键.
13.-3
【分析】
根据正负数的意义即可得出结论.
【详解】
解:若元表示收入5元,则支出3元记作-3元
故答案为:-3.
【点睛】
本题考查了正数和负数,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
14.0.52x
【分析】
求出女生人数占总人数的百分率,然后乘总人数即可.
【详解】
解:女生人数占总人数的1-48%=52%
∴女生人数是52%x=0.52x
故答案为:0.52x.
【点睛】
此题考查的是用代数式表示实际意义,解答本题的关键是正确理解文字语言中的关键词,从而明确其中的运算关系,正确地列出代数式.
15.-2
【分析】
根据平方和绝对值的非负性即可求出a和b的值,然后代入求值即可.
【详解】
解:∵,
∴
解得:
∴==-2
故答案为:-2.
【点睛】
此题考查的是非负性的应用,掌握平方和绝对值的非负性是解题关键.
16.5×107
【分析】
根据科学记数法的定义:将一个数字表示成 a×10n的形式,其中1≤|a|<10,n表示整数,这种记数方法叫科学记数法,即可得出结论.
【详解】
解:5000万=50000000=5×107
故答案为:5×107.
【点睛】
此题考查的是科学记数法,掌握科学记数法的定义是解题关键.
17.
【分析】
根据数轴可以得到a、b的正负情况,得出a+b>0,从而可以化简题目中的式子,本题得以解决.
【详解】
解:由数轴可知:-1<a<0,b>1
∴a+b>0
∴
=
=
=
故答案为:.
【点睛】
本题考查了数轴上点的特点、绝对值的化简.解决本题的关键是根据数轴上点的位置,判断a、b与a+b的正负.
18.3
【分析】
先将原式去括号、合并同类项,然后利用整体代入法求值即可.
【详解】
解:∵,
∴
=
=
=2-(-1)
=3
故答案为:3.
【点睛】
此题考查的是整式的化简求值,掌握去括号法则、合并同类项法则和整体代入法是解题关键.
19.见解析
【分析】
根据整数的定义、负数的定义、负分数的定义和非负数的定义分类即可.
【详解】
解:整数集合:;
负数集合:;
负分数集合:;
非负数集合:.
【点睛】
此题考查的是有理数的分类,掌握整数的定义、负数的定义、负分数的定义和非负数的定义是解题关键.
20.(1);(2)
【分析】
(1)根据乘法分配律、有理数的乘法法则和减法法则计算即可;
(2)根据有理数的运算顺序和各个运算法则计算即可.
【详解】
解:(1)
=
=
=
(2)
=
=
=
【点睛】
本题考查了有理数的混合运算,解题的关键是掌握各个运算法则和运算律.
21.数轴见解析,<<<
【分析】
先将各数能化简的化简,然后补全数轴并在数轴上标出各数,最后利用数轴比较大小即可.
【详解】
解:=-3,=3
由数轴可知:<<<.
【点睛】
此题考查的是利用数轴表示数和比较大小,掌握数轴上的数从左至右逐渐变大是解题关键.
22.;8
【分析】
先根据去括号法则和合并同类项法则化简,然后代入求值即可.
【详解】
解:
=
=
=
当,时,
原式==8.
【点睛】
此题考查的是整式的化简求值,掌握去括号法则和合并同类项法则是解题关键.
23.(1)296(2)最多的一天比最少的一天多销售29千克;(3)2868元.
【分析】
(1)求出前三天的总差值,再加上300千克即可;
(2)找出卖出最多的与最少的千克数,相减即可;
(3)根据题意列出算式,计算即可求出值.
【详解】
(1)根据题意得:100×3+4-3-5=296(千克);
(2)千克
答:最多的一天比最少的一天多销售29千克
(3)千克
(17+100×7)×(5-1)=717×4=2868(元).
答:小明本周一共收入2868元.
【点睛】
此题考查了正数与负数,熟练掌握运算法则是解本题的关键.
24.当x>1000时,甲商场需付款200+0.8x;乙商场需付款80+0.9x;(2)在甲商场购买比较合算.
【分析】
(1)当x>1000时:在甲商场的费用是:1000+超过1000元的部分×80%;在乙商场的费用是:800+超过800元的部分×90%
(2)计算出当x=1500时两家商场的费用并比较即可.
【详解】
(1)当x>1000时,甲商场需付款1000+80% (x-1000)=200+0.8x
乙商场需付款800+90% (x-800)=80+0.9x
(2)当x=1500时,甲商场需付款200+0.8x=200+0.8×1500=1400(元)
乙商场需付款80+0.9x=80+0.9×1500=1430(元)
因此,在甲商场购买比较合算.
【点睛】
此题主要考查了根据实际问题列代数式,关键是正确理解题意,分清两个商场的收费方式.
25.(1)2;6;8;(2)①AB=3t+2,BC=3t+6,AC=6t+8;②不变,其值为4.
【分析】
(1)根据各个点在数轴上表示的数,即可求出AB、BC、AC的长,
(2)①用含有t的代数式表示出运动后,点A、B、C所表示的数,进而表示AB、BC、AC,
②根据BC、AB的长,计算BC-AB的值,得出结论.
【详解】
解:(1)由数轴可知:AB=|-2-0|=2,BC=|0-6|=6,AC=|-2-6|=8,
故答案为:2;6;8.
(2)①由题意可知:移动t秒后,点A所表示的数为(-2-t),点B所表示的数为2t,点C所表示的数为(6+5t),
因此,AB=2t-(-2-t)=3t+2,BC=(6+5t)-2t=3t+6,AC=6+5t-(-2-t)=6t+8;
②不变,
BC-AB=3t+6-(3t+2)=4,
答:BC-AB的值不会随着运动时间t的变化而变化,其值为4.
【点睛】
考查数轴表示数的意义,根据数轴上点所表示的数,求两点之间的距离是常见的题型.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.的相反数是( )
A. B.2020 C. D.
2.下列各数种,比小的数是( )
A. B. C.0 D.3
3.用四舍五入法对1.8935取近似值,若精确到0.001,则下列各数种,正确的是( )
A.1.890 B.1.893 C.1.894 D.1.89
4.天气预报,某月5日的气温是-3℃~5℃.则这天的温差(最高气温减最低气温,单位:℃)是( )
A.8 B.2 C. D.
5.数轴上,点A表示的数是1,点与点距离2个单位长度,则点表示的数是( )
A.3 B. C.2 D.3或
6.下列不是同类项的是( )
A.和 B.和
C.和 D.和
7.下列各组有理数的大小比较中,正确的是( )
A. B.
C. D.
8.下列各式中,去括号正确的是( )
A. B.
C. D.
9.下列各式的计算,正确的是( )
A. B.
C. D.
10.若单项式与的和仍为单项式,则的值是( )
A.1 B.-1 C.5 D.-5
11.如图是一台数值转换机,若输入的值为,则输出的结果为( )
A. B. C.1 D.
12.观察下列关于的单项式:,,,……,按照上述规律,第100个单项式是( )
A. B. C. D.
二、填空题
13.若元表示收入5元,则支出3元记作______元.
14.全校学生总数是,其中男生占总人数的48%,则女生人数是______.
15.若,则的值为______.
16.截至2020年11月9日,全球新冠肺炎累计确诊病例超过5000万例,5000万用科学记数法表示为______.
17.有理数,在数轴上对应点的位置如图所示,则式子的的化简结果为______.
18.“整体思想”是数学中的一种重要的思想方法,它在数学运算、推理中有广泛的应用.如:已知,,则.利用上述思想方法计算:已知,.则______.
三、解答题
19.将下列各数填在相应的集合内:2.1,0,,,365,,.
整数集合:;
负数集合:;
负分数集合:;
非负数集合:.
20.计算:
(1); (2).
21.如图是一条不完整的数轴,请你补充完整,并在数轴上标出下列各数,然后把这些数用“<”连接起来:,,.
22.先化简,再求值:,其中,.
23.在互联网技术的影响下,幸福新村的村民小刘在网上销售苹果,原计划每天卖100千克,但实际每天的销量与计划销量相比有出入,如表是某周的销售情况(超额记为正,不足记为负.单位:千克):
星期
一
二
三
四
五
六
日
与计划量的差值
(1)根据表中的数据可知前三天共卖出___________千克;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售多少千克?
(3)若每千克按5元出售,每千克苹果的运费为1元,那么小刘本周一共收入多少元?
24.甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同,甲商场规定:凡超过元的电器,超出的金额按收取;乙商场规定:凡超过元的电器,超出的金额按收取,某顾客购买的电器价格是元.
(1)当时,分别用代数式表示在两家商场购买电器所需付的费用
(2)当时,该顾客应选择哪一家商场购买比较合算?说明理由.
25.如图所示,在数轴上点,,表示的数分别为,0,6.点与点之间的距离表示为,点与点之间的距离表示为,点与点之间的距离表示为.
(1)______,______,______;
(2)点,,开始在数轴上运动,若点以每秒1个单位长度的速度向左运动,同时点和点分别以每秒2个单位长度和5个单位长度的速度向右运动.
①设运动时间为,请用含有的算式分别表示出,,;
②在①的条件下,请问:的值是否随着运动时间的变化而变化?若变化,请说明理由;若不变,请求其值.
参考答案
1.B
【分析】
根据相反数的定义:只有符号不同的两个数互为相反数,即可得出结论.
【详解】
解:的相反数是:2020.
故选B.
【点睛】
此题考查的是求一个数的相反数,掌握相反数的定义是解题关键.
2.A
【分析】
先根据正数都大于0,负数都小于0,可排除C、D,再根据两个负数,绝对值大的反而小,即可得出结论.
【详解】
解:先根据正数都大于0,负数都小于0,可排除C、D,
∵=4,=3,,而4>3>2
∴<<
∴各选项中,比小的数是
故选A.
【点睛】
此题考查的是有理数的比较大小,掌握正数都大于0;负数都小于0;两个负数,绝对值大的反而小,是解题关键.
3.C
【分析】
把1.8935千分位上的5四舍五入即可.
【详解】
解:精确到0.001,1.8935≈1.894
故选C.
【点睛】
此题考查的是求一个数的近似数,掌握四舍五入法是解题关键.
4.A
【分析】
根据温差=最高气温-最低气温和有理数的减法法则计算即可.
【详解】
解:这天的温差为5-(-3)=8℃
故选A.
【点睛】
此题考查的是有理数减法的应用,掌握温差=最高气温-最低气温是解题关键.
5.D
【分析】
先根据点A和点B的位置分类讨论,再根据点A表示的数和A、B两点的距离分别求解即可.
【详解】
解:若点B在点A的左侧,
∵点A表示的数是1,点与点距离2个单位长度,
∴点B表示的数为1-2=-1;
若点B在点A的右侧,
∵点A表示的数是1,点与点距离2个单位长度,
∴点B表示的数为1+2=3;
综上:点B表示的数为3或
故选D.
【点睛】
此题考查的是根据数轴上两点的距离和一点所表示的数,求另一点所表示的数,掌握分类讨论是数学思想和数轴上两点之间的距离公式是解题关键.
6.C
【分析】
根据同类项的定义:如果两个单项式,它们所含的字母相同,并且相同字母的指数也分别相同,那么就称这两个单项式为同类项,逐一判断即可.
【详解】
解:A.或是同类项,故不符合题意;
B.和是同类项,故不符合题意;
C.和不是同类项,故符合题意;
D.和是同类项,故不符合题意.
故选C.
【点睛】
此题考查的是同类项的判断,掌握同类项的定义是解题关键.
7.C
【分析】
先将多重符号和绝对值化简,然后根据有理数的比较大小方法逐一判断即可.
【详解】
解:A.,而1>-2,所以,故错误;
B.,而-3<2,所以,故错误;
C.,而,所以,故正确;
D. ,而,所以,故错误.
故选C.
【点睛】
此题考查的是有理数的比较大小,解题关键是先将多重符号和绝对值化简.
8.C
【分析】
各式去括号得到结果,即可作出判断.
【详解】
解:,故A错误;
,故B,D错误,C正确.
故选:C.
【点睛】
此题考查了去括号与添括号,熟练掌握去括号法则是解本题的关键.
9.D
【分析】
根据同类项的定义和合并同类项法则逐一判断即可.
【详解】
解:A.,故本选项错误;
B.和不是同类项,不能合并,故错误;
C.和不是同类项,不能合并,故错误;
D.,故正确.
故选D.
【点睛】
此题考查的是同类项的判断和合并同类项,掌握同类项的定义和合并同类项法则是解题关键.
10.B
【详解】
∵单项式x2yn与-2xmy3的和仍为单项式,
∴它们是同类项,
∴m=2,n=3,
∴m-n=-1.
故选B.
【点睛】
同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同,从而得出m,n的值.
11.C
【分析】
根据数值转换机的运算规则计算即可.
【详解】
解:根据题意可得:[(-5)-(-2)]÷(-3)=(-3) ÷(-3)= 1.
故选C.
【点睛】
此题考查的是有理数的混合运算,掌握有理数的各个运算法则是解题关键.
12.D
【分析】
根据已知单项式的排列规律,推出第n个单项式,从而求出结论.
【详解】
解:∵=
=
=
∴第n个单项式为
∴第100个单项式是
故选D.
【点睛】
此题考查的是探索规律题,找出规律并归纳公式是解题关键.
13.-3
【分析】
根据正负数的意义即可得出结论.
【详解】
解:若元表示收入5元,则支出3元记作-3元
故答案为:-3.
【点睛】
本题考查了正数和负数,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
14.0.52x
【分析】
求出女生人数占总人数的百分率,然后乘总人数即可.
【详解】
解:女生人数占总人数的1-48%=52%
∴女生人数是52%x=0.52x
故答案为:0.52x.
【点睛】
此题考查的是用代数式表示实际意义,解答本题的关键是正确理解文字语言中的关键词,从而明确其中的运算关系,正确地列出代数式.
15.-2
【分析】
根据平方和绝对值的非负性即可求出a和b的值,然后代入求值即可.
【详解】
解:∵,
∴
解得:
∴==-2
故答案为:-2.
【点睛】
此题考查的是非负性的应用,掌握平方和绝对值的非负性是解题关键.
16.5×107
【分析】
根据科学记数法的定义:将一个数字表示成 a×10n的形式,其中1≤|a|<10,n表示整数,这种记数方法叫科学记数法,即可得出结论.
【详解】
解:5000万=50000000=5×107
故答案为:5×107.
【点睛】
此题考查的是科学记数法,掌握科学记数法的定义是解题关键.
17.
【分析】
根据数轴可以得到a、b的正负情况,得出a+b>0,从而可以化简题目中的式子,本题得以解决.
【详解】
解:由数轴可知:-1<a<0,b>1
∴a+b>0
∴
=
=
=
故答案为:.
【点睛】
本题考查了数轴上点的特点、绝对值的化简.解决本题的关键是根据数轴上点的位置,判断a、b与a+b的正负.
18.3
【分析】
先将原式去括号、合并同类项,然后利用整体代入法求值即可.
【详解】
解:∵,
∴
=
=
=2-(-1)
=3
故答案为:3.
【点睛】
此题考查的是整式的化简求值,掌握去括号法则、合并同类项法则和整体代入法是解题关键.
19.见解析
【分析】
根据整数的定义、负数的定义、负分数的定义和非负数的定义分类即可.
【详解】
解:整数集合:;
负数集合:;
负分数集合:;
非负数集合:.
【点睛】
此题考查的是有理数的分类,掌握整数的定义、负数的定义、负分数的定义和非负数的定义是解题关键.
20.(1);(2)
【分析】
(1)根据乘法分配律、有理数的乘法法则和减法法则计算即可;
(2)根据有理数的运算顺序和各个运算法则计算即可.
【详解】
解:(1)
=
=
=
(2)
=
=
=
【点睛】
本题考查了有理数的混合运算,解题的关键是掌握各个运算法则和运算律.
21.数轴见解析,<<<
【分析】
先将各数能化简的化简,然后补全数轴并在数轴上标出各数,最后利用数轴比较大小即可.
【详解】
解:=-3,=3
由数轴可知:<<<.
【点睛】
此题考查的是利用数轴表示数和比较大小,掌握数轴上的数从左至右逐渐变大是解题关键.
22.;8
【分析】
先根据去括号法则和合并同类项法则化简,然后代入求值即可.
【详解】
解:
=
=
=
当,时,
原式==8.
【点睛】
此题考查的是整式的化简求值,掌握去括号法则和合并同类项法则是解题关键.
23.(1)296(2)最多的一天比最少的一天多销售29千克;(3)2868元.
【分析】
(1)求出前三天的总差值,再加上300千克即可;
(2)找出卖出最多的与最少的千克数,相减即可;
(3)根据题意列出算式,计算即可求出值.
【详解】
(1)根据题意得:100×3+4-3-5=296(千克);
(2)千克
答:最多的一天比最少的一天多销售29千克
(3)千克
(17+100×7)×(5-1)=717×4=2868(元).
答:小明本周一共收入2868元.
【点睛】
此题考查了正数与负数,熟练掌握运算法则是解本题的关键.
24.当x>1000时,甲商场需付款200+0.8x;乙商场需付款80+0.9x;(2)在甲商场购买比较合算.
【分析】
(1)当x>1000时:在甲商场的费用是:1000+超过1000元的部分×80%;在乙商场的费用是:800+超过800元的部分×90%
(2)计算出当x=1500时两家商场的费用并比较即可.
【详解】
(1)当x>1000时,甲商场需付款1000+80% (x-1000)=200+0.8x
乙商场需付款800+90% (x-800)=80+0.9x
(2)当x=1500时,甲商场需付款200+0.8x=200+0.8×1500=1400(元)
乙商场需付款80+0.9x=80+0.9×1500=1430(元)
因此,在甲商场购买比较合算.
【点睛】
此题主要考查了根据实际问题列代数式,关键是正确理解题意,分清两个商场的收费方式.
25.(1)2;6;8;(2)①AB=3t+2,BC=3t+6,AC=6t+8;②不变,其值为4.
【分析】
(1)根据各个点在数轴上表示的数,即可求出AB、BC、AC的长,
(2)①用含有t的代数式表示出运动后,点A、B、C所表示的数,进而表示AB、BC、AC,
②根据BC、AB的长,计算BC-AB的值,得出结论.
【详解】
解:(1)由数轴可知:AB=|-2-0|=2,BC=|0-6|=6,AC=|-2-6|=8,
故答案为:2;6;8.
(2)①由题意可知:移动t秒后,点A所表示的数为(-2-t),点B所表示的数为2t,点C所表示的数为(6+5t),
因此,AB=2t-(-2-t)=3t+2,BC=(6+5t)-2t=3t+6,AC=6+5t-(-2-t)=6t+8;
②不变,
BC-AB=3t+6-(3t+2)=4,
答:BC-AB的值不会随着运动时间t的变化而变化,其值为4.
【点睛】
考查数轴表示数的意义,根据数轴上点所表示的数,求两点之间的距离是常见的题型.
同课章节目录
