山东省烟台招远市(五四制)2020-2021学年七年级上学期期中数学试题(Word版 含解析)
文档属性
| 名称 | 山东省烟台招远市(五四制)2020-2021学年七年级上学期期中数学试题(Word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 436.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览

文档简介
山东省烟台招远市(五四制)2020-2021学年七年级上学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
2.下列说法不正确的是( )
A.在角的内部,角平分线上的点到这个角两条边的距离相等
B.线段的垂直平分线上的点到这条线段的两个端点的距离相等
C.圆有无数条对称轴
D.等腰三角形的对称轴是底角的平分线所在的直线
3.已知在△?ABC?中,?AB?=?8?,?BC?=?15?,?AC?=?17?,则下列结论错误的是?(? ?)
A.△?ABC?是直角三角形,且∠?B?=?90° B.△?ABC?是直角三角形,且∠?A?=?60°
C.△?ABC?是直角三角形,且?AC?是它的斜边 D.△?ABC?的面积为?60
4.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
A. B.
C. D.
5.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.若AC=5,则DF=___.
A.10 B.6 C.5 D.2
6.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是()
A.CD、EF、GH B.AB、EF、GH C.AB、CD、GH D.AB、CD、EF
7.如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( )
A.65度 B.115度 C.90度 D.75度
8.如图,将RtABC绕直角项点C顺时针旋转90°,得到A' B'C,连接AA',若∠1=20°,则∠B的度数是( )
A.70° B.65° C.60° D.55°
9.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
10.如图所示,正方形和正方形的面积分别是100和36,则以为直径的半圆的面积是( )
A. B. C. D.
11.如图,△ABC中,AB=AC,DE是线段AB的垂直平分线,如果BD+CD=2020,那么AB的长度是( )
A.1010 B.2019 C.2020 D.2021
12.如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为( )
A.115cm B.125cm C.135cm D.145cm
二、填空题
13.如图,,要使,还需添加一个条件是:______.(填上你认为适当的一个条件即可)
14.一个直角三角形的木板,三边的平方和3200,则其斜边为 __________________
15.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,垂足为A,B,S△AOM=8cm2,OA=4cm,则MB=___.
16.如图,点E在正方形ABCD的边AB上,若EB=2,EC=5,那么正方形ABCD的面积为______________
17.小敏设计了一种挂衣架,在挂衣服的时候可以任意角度收扰两个挂衣杆和,然后套进衣服后松开即可.如图1,衣架杆OA=OB.如图2,若衣架收拢时衣服领口宽AB=22cm,且∠AOB=60°,那么这个衣架杆的长OA=OB=______.
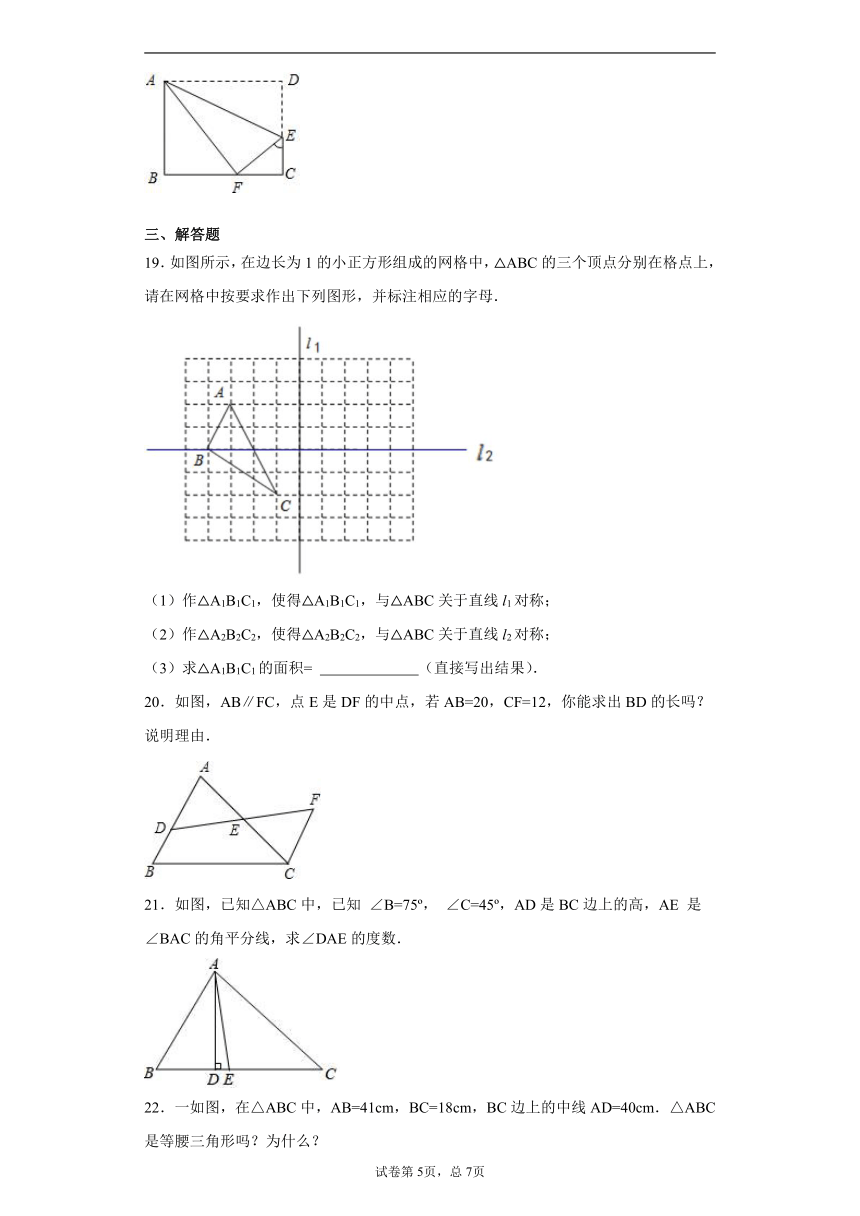
18.七年级某班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=10cm,宽AB=8cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长度为 ___________________.
三、解答题
19.如图所示,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.
(1)作△A1B1C1,使得△A1B1C1,与△ABC关于直线l1对称;
(2)作△A2B2C2,使得△A2B2C2,与△ABC关于直线l2对称;
(3)求△A1B1C1的面积= (直接写出结果).
20.如图,AB∥FC,点E是DF的中点,若AB=20,CF=12,你能求出BD的长吗?说明理由.
21.如图,已知△ABC中,已知 ∠B=75?, ∠C=45?,AD是BC边上的高,AE 是∠BAC的角平分线,求∠DAE的度数.
22.一如图,在△ABC中,AB=41cm,BC=18cm,BC边上的中线AD=40cm.△ABC是等腰三角形吗?为什么?
23.为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路的一侧点处有一村庄,村庄到公路的距离为800米,假使宣讲车周围1000米以内能听到广播宣传,宣讲车在公路上沿方向行驶时:
(1)请问村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?
24.Rt△AB C中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).当t为何值时,△ABP为直角三角形?
25.问题情境:已知Rt△ABC的周长为56,斜边长c=25,求△ABC的面积.
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c= ___,
因为c=25,所以a+b=___,
所以(a+b)2=___,
所以a2+ ___=961
因为a2+b2=c2,
所以c2+2ab=961,
所以 ___+2ab=961,
所以ab= 168(第1步)
所以△ABC的面积=ab=× 168= 84(第2步).
合作探究:
(1)填空:填写题目中横线处的内容.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是 ___(填序号).
①整体思想; ②数形结合思想; ③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为6,斜边长为5,求这个直角三角形的周长.
参考答案
1.D
【分析】
根据轴对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
【详解】
A、不是轴对称图形,故A不符合题意;
B、不是轴对称图形,故B不符合题意;
C、不是轴对称图形,故C不符合题意;
D、是轴对称图形,故D符合题意.
故选D.
【点睛】
本题主要考查轴对称图形的知识点.确定轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.D
【分析】
由题意根据角平分线的性质、线段的垂直平分线的性质、轴对称的性质以及等腰三角形性质,利用排除法进行分析即可.
【详解】
解:A. 角平分线上的点到这个角两条边的距离相等,此选项正确;
B. 线段的垂直平分线上的点到这条线段的两个端点的距离相等,此选项正确;
C. 过圆心的直线都是圆的对称轴,而过圆心的直线有无数条,此选项正确;
D. 等腰三角形的对称轴是顶角的平分线所在的直线而不是底角的平分线所在的直线,此选项不正确.
故选:D.
【点睛】
本题主要考查角平分线的性质、线段的垂直平分线的性质、全等三角形判定以及等腰三角形性质,理解相关的性质是解答本题的关键.
3.B
【分析】
先根据勾股定理的逆定理判断出△ABC的形状,再根据直角三角形的性质进行逐一判断即可.
【详解】
解:∵△ABC中,AB=8,BC=15,AC=17,
∴AB2+BC2=82+152=AC2=172,
∴△ABC是直角三角形,AC为斜边,
∴A、C正确;
∵△ABC是直角三角形,
∴S△ABC=×8×15=60,故D正确;
根据三角形三边关系判断∠A≠60°,故B错误
故选:B
【点睛】
本题考查的是勾股定理的逆定理及直角三角形的性质,根据题意判断出△ABC的形状是解答此题的关键.
4.B
【分析】
认真观察各选项给出的图形,根据轴对称的性质,对称轴垂直平分线对应点的连线进行判断.
【详解】
根据轴对称的性质,结合四个选项,只有B选项中对应点的连线被对称轴MN垂直平分,所以B是符合要求的.
故选:B.
【点睛】
本题考查轴对称的性质;应用对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分解题是正确解答本题的关键.
5.C
【分析】
根据BE=CF,求出BC=EF,根据AAS推出△ABC≌△DEF,根据全等三角形的性质推出对应边相等即可.
【详解】
∵BE=CF,
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS),
∴AC=DF=5(全等三角形对应边相等).
故选C.
【点睛】
本题考查了全等三角形的性质和判定的应用,解此题的关键是推出△ABC≌△DEF,注意:全等三角形的对应边相等.
6.B
【分析】
设出正方形的边长,利用勾股定理,解出AB、CD、EF、GH各自的长度,再由勾股定理的逆定理分别验算,看哪三条边能够成直角三角形.
【详解】
解:设小正方形的边长为1,
则AB2=22+22=8,
CD2=22+42=20,
EF2=12+22=5,
GH2=22+32=13.
因为AB2+EF2=GH2,
所以能构成一个直角三角形三边的线段是AB、EF、GH.
故选:B.
【点睛】
本题考查了勾股定理逆定理的应用;解题的关键是解出AB、CD、EF、GH各自的长度.
7.C
【分析】
根据折叠的性质和矩形的性质得出∠CBA=∠CBA′,∠CAD=90°,根据角平分线的性质得出∠A′BE=∠DBE,求出∠CBE=∠CBA′+∠A′BE=∠ABD,代入求出即可.
【详解】
解:∵将长方形纸片的一角折叠,使顶点A落在点A′处,
∴∠CBA=∠CBA′=∠ABA′,∠CAD=90°,
∵BE是∠A′BD的平分线,
∴∠A′BE=∠DBE=∠A′BD,
∴∠CBE=∠CBA′+∠A′BE
= ∠ABA′+ ∠A′BD
= (∠ABA′+∠A′BD)
= ∠ABD
= ×180°
=90°,
故选:C.
【点睛】
本题考查了矩形的性质,折叠的性质,角平分线定义等知识点,关键是求出∠CBE=∠ABD.
8.B
【分析】
根据图形旋转的性质得AC=A′C,∠ACA′=90°,∠B=∠A′B′C,从而得∠AA′C=45°,结合∠1=20°,即可求解.
【详解】
∵将RtABC绕直角项点C顺时针旋转90°,得到A' B'C,
∴AC=A′C,∠ACA′=90°,∠B=∠A′B′C,
∴∠AA′C=45°,
∵∠1=20°,
∴∠B′A′C=45°-20°=25°,
∴∠A′B′C=90°-25°=65°,
∴∠B=65°.
故选B.
【点睛】
本题主要考查旋转的性质,等腰三角形和直角三角形的性质,掌握等腰三角形和直角三角形的性质定理,是解题的关键.
9.C
【详解】
要使△ABP与△ABC全等,必须使点P到AB的距离等于点C到AB的距离,即3个单位长度,所以点P的位置可以是P1,P2,P4三个,故选C.
10.B
【分析】
根据两个正方形的面积求得AB与BD的长度,根据勾股定理求得直角三角形中AD的长度,从而根据圆的面积公式求得半圆的面积.
【详解】
由题意可得,BD=6,AB=10,
则在直角三角形ABC中,AD=8,
则以AD为直径的半圆的面积为:.
故选B
【点睛】
本题考查了正方形与勾股定理的综合运用,利用正方形的面积求出AB与BD的长度是解题的关键.
11.C
【分析】
根据DE是线段AB的垂直平分线,得到BD=AD,便可求解.
【详解】
解:DE是线段AB的垂直平分线
∴BD=AD
∵BD+CD=2020
∴AD+CD=2020 即AC=2020
∵AB=AC
∴AB=2020
故选C.
【点睛】
本题考查等腰三角形性质,以及线段垂直平分线性质,属于基础题.
12.B
【分析】
把立体几何图展开得到平面几何图,如图,然后利用勾股定理计算AB,则根据两点之间线段最短得到蚂蚁所走的最短路线长度.
【详解】
解:展开图为:
则AC=100cm,BC=15×3+10×3=75cm,
在Rt△ABC中,AC=100cm,∴AB==125cm.
所以蚂蚁所走的最短路线长度为125cm.
故选:B.
【点睛】
本题考查了勾股定理的应用,把立体几何图中的问题转化为平面几何图中的问题是解题的关键.
13.或或
【分析】
由∠1=∠2可得∠AEB=∠AEC,AD为公共边,根据全等三角形的判定添加条件即可.
【详解】
∵∠1=∠2,
∴∠AEB=∠AEC,
∵AE为公共边,
∴根据“SAS”得到三角形全等,可添加BE=CE;根据“AAS”可添加∠B=∠C;根据“ASA”可添加∠BAE=∠CAE;
故答案为:BE=CE或∠B=∠C或∠BAE=∠CAE.
【点睛】
本题考查全等三角形的判定,全等三角形的常用的判定方法有SSS、SAS、AAS、ASA、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.熟练掌握全等三角形的判定定理是解题的关键.
14.40
【分析】
设这个直角三角形木板的两直角边长为a、b,斜边为c,然后根据勾股定理及题意可进行求解.
【详解】
解:设这个直角三角形木板的两直角边长为a、b,斜边为c,根据题意得:
,
∴,
∴;
故答案为40.
【点睛】
本题主要考查勾股定理,熟练掌握勾股定理是解题的关键.
15.4cm
【分析】
根据求得AM的长度,利用角平分线上的点到角两边的距离相等即可求解.
【详解】
解:,
解得,
∵OM平分∠POQ,
∴,
故答案为:4cm.
【点睛】
本题考查角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键.
16.21
【分析】
先根据正方形的性质得出∠B=90°,然后在Rt△BCE中,利用勾股定理得出BC2,即可得出正方形的面积.
【详解】
解:∵四边形ABCD是正方形,
∴∠B=90°,
∴BC2=EC2-EB2=52-22=21,
∴正方形ABCD的面积=BC2=21.
故答案为:21.
【点睛】
本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.即如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.也考查了正方形的性质.
17.22
【分析】
图一、图二∠AOB的度数发生变化,但是OA、OB的长度没有改变,在通过∠AOB=60°,OA=OB,得到三角形AOB为等边三角形求解.
【详解】
图一、图二∠AOB的度数发生变化,但是OA、OB的长度没有改变,任然有OA=OB.
∵OA=OB,∠AOB=60°,
∴△AOB为等边三角形,
∴OA=OB=AB=22cm.
【点睛】
本题比较简单,主要是对三角形中等腰、等边三角形的考查,熟练掌握这块的基础知识是解答本题的关键.
18.3cm
【分析】
根据矩形的性质和翻折的性质可得AF=AD=10cm,EF=DE,设EC=xcm,则DE=(8-x)cm,在Rt△ABF中,由勾股定理可得BF的长,继而求得CF的长,在Rt△EFC中,由勾股定理可得关于x的一元二次方程,解方程即可.
【详解】
解:∵四边形ABCD是矩形,BC=10cm,AB=8cm
∴∠B=∠C=90°,AB=CD=8cm,BC=AD=10cm,
根据翻折的性质可得AF=AD=10cm,EF=DE,
设EC=xcm,则EF=DE=(8-x)cm,
在Rt△ABF中,由勾股定理可得: BF
BF,
∴CF=BC-BF=10-6=4cm,
在Rt△EFC中,由勾股定理可得:
即.
解得:
即:EC=3cm
故答案为:3cm
【点睛】
本题主要考查矩形的性质、翻折的性质、勾股定理的应用,解题的关键是根据勾股定理列出.
19.(1)见解析;(2)见解析;(3)4
【分析】
(1)根据轴对称图形的性质进行作图即可;
(2)根据轴对称图形的性质进行作图即可;
(3)利用割补法求解即可.
【详解】
(1)如图,△A1B1C1与△ABC关于直线l1对称;
(2)如图,△A2B2C2与△ABC关于直线l2对称;
(3).
【点睛】
本题考查了轴对称作图及三角形面积的求解,能够准确根据题目要求作出对称图形,及熟练运用割补法求解三角形面积是解决问题的关键.
20.8,理由见解析
【分析】
由题意易得DE=FE,∠A=∠ECF,∠ADE=∠F,进而可证△ADE≌△CFE,则有CF=AD,然后问题可求解.
【详解】
解:BD=8,理由如下:
∵AB∥FC,
∴∠A=∠ECF,∠ADE=∠F,
∵点E是DF的中点,
∴DE=FE,
∴△ADE≌△CFE(AAS),
∴CF=AD,
∵AB=20,CF=12,
∴.
【点睛】
本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
21.15?
【分析】
由三角形的内角和定理,可求∠BAC=60°,又由AE是∠BAC的平分线,可求∠BAE=30°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=15°,所以∠DAE=∠BAE-∠BAD=15°.
【详解】
解:∵ ∠B=75? ,∠C=45?
∴∠BAC=60?
∵ AE是∠BAC的角平分线
∴∠BAE=∠BAC=30?
∵ AD是BC边上的角高
∴∠BAD=90?-∠B=90?-75?=15?
∴∠DAE=∠BAE-∠BAD=30?-15?=15?
【点睛】
本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和180°.
22.△ABC是等腰三角形,理由见解析.
【分析】
由已知可得BD的长,再根据勾股定理的逆定理可判定AD垂直BC,从而可利用勾股定理求得AC的长,此时发现AB=AC,即该三角形是等腰三角形.
【详解】
解:△ABC是等腰三角形,理由如下:
∵BC=18cm,BC边上的中线为AD,
∴BD=CD=9cm.
∵AB=41cm,BD=9cm,AD=40cm,
∴AB2=1681,BD2+AD2=1681,
∴AB2=BD2+AD2,
∴AD⊥BC.
∵BD=CD,
∴AC=AB,
∴△ABC是等腰三角形.
23.(1)村庄能听到宣传. 理由见解析;(2)村庄总共能听到4分钟的宣传.
【分析】
(1)根据题意村庄A到公路MN的距离为800米<1000米,即可解答
(2)假设当宣讲车行驶到P点开始影响村庄,行驶Q点结束对村庄的影响
【详解】
解:(1)村庄能听到宣传.
理由:因为村庄A到公路MN的距离为800米<1000米,所以村庄能听到宣传
(2)如图,假设当宣讲车行驶到P点开始影响村庄,行驶Q点结束对村庄的影响,利用勾股定理进行计算即可解答
则AP=AQ=1000米,AB=800米.
∴BP=BQ==600米.
∴PQ=1200米.
、∴影响村庄的时间为:1200÷300=4(分钟).
∴村庄总共能听到4分钟的宣传.
【点睛】
此题考查解直角三角形,利用勾股定理进行计算是解题关键
24.4或12.5
【分析】
分当∠AP1B=90°,△ABP1为直角三角形时和当∠BAP2=90°,△ABP2为直角三角形时两种情况讨论即可.
【详解】
解:在Rt△ABC中,由勾股定理得:
BC2+AC2=AB2
∴BC2+62=102
∴BC=8,
当∠AP1B=90°,△ABP1为直角三角形时,P1在C处,即BP1=8,
∴8÷2=4(s);
当∠BAP2=90°,△ABP2为直角三角形时,
设BP2为x,则CP2=x-8
在△ACP2中,由勾股定理得:
AC2+CP22=AP22
∴62+(x-8)2=AP22
在△BAP2中,由勾股定理得:
AB2+AP22=BP22
∴AP22= BP22- AB2=x2-102
∴x2-102=62+(x-8)2
∴x=12.5.
【点睛】
本题考查了勾股定理,解答本题的关键是掌握勾股定理的应用.
25.(1)56,31,961,2ab+b2,625;(2)①;(3)12
【分析】
(1)根据三角形的周长定义,勾股定理,三角形的面积公式即可求解;
(2)根据(1)的解答过程得到由第1步到第2步体现出来的数学思想;
(3)设直角三角形的两直角边分别是a、b(a<b,且a、b均为正数).利用勾股定理和三角形的面积公式求得两直角边是6和8.然后由三角形的周长公式求得该直角三角形的周长.
【详解】
解:(1)∵Rt△ABC的周长为56,
∴a+b+c=56,
∵c=25,
∴a+b=31,
∴(a+b)2=961,
∴a2+2ab+b2=961
∵a2+b2=c2,
∴c2+2ab=961,
∴625+2ab=961,
∴ab= 168(第1步)
∴△ABC的面积=ab=× 168= 84(第2步).
故答案为:①56 ②31 ③961(填312也可以) ④2ab+b2 ⑤625
(2)∵由第1步到第2步中用了整体代入,
∴体现的数学思想是①.
故答案为①.
(3)设直角三角形的两直角边分别是a、b, 斜边为c
∵三角形面积为6
∴ab=6,
∴2ab=24
∵a2+b2=c2
∴a2+2ab+b2=52 +2ab
∴(a+b)2=25+24=49
∵a+b?0
∴ a+b=7
所以这个直角三角形的周长是:a+b+c=7+5=12.
【点睛】
本题主要考查了利用三角形的面积公式寻找相等关系,同时也考查了勾股定理的内容.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
2.下列说法不正确的是( )
A.在角的内部,角平分线上的点到这个角两条边的距离相等
B.线段的垂直平分线上的点到这条线段的两个端点的距离相等
C.圆有无数条对称轴
D.等腰三角形的对称轴是底角的平分线所在的直线
3.已知在△?ABC?中,?AB?=?8?,?BC?=?15?,?AC?=?17?,则下列结论错误的是?(? ?)
A.△?ABC?是直角三角形,且∠?B?=?90° B.△?ABC?是直角三角形,且∠?A?=?60°
C.△?ABC?是直角三角形,且?AC?是它的斜边 D.△?ABC?的面积为?60
4.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
A. B.
C. D.
5.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.若AC=5,则DF=___.
A.10 B.6 C.5 D.2
6.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是()
A.CD、EF、GH B.AB、EF、GH C.AB、CD、GH D.AB、CD、EF
7.如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( )
A.65度 B.115度 C.90度 D.75度
8.如图,将RtABC绕直角项点C顺时针旋转90°,得到A' B'C,连接AA',若∠1=20°,则∠B的度数是( )
A.70° B.65° C.60° D.55°
9.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
10.如图所示,正方形和正方形的面积分别是100和36,则以为直径的半圆的面积是( )
A. B. C. D.
11.如图,△ABC中,AB=AC,DE是线段AB的垂直平分线,如果BD+CD=2020,那么AB的长度是( )
A.1010 B.2019 C.2020 D.2021
12.如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为( )
A.115cm B.125cm C.135cm D.145cm
二、填空题
13.如图,,要使,还需添加一个条件是:______.(填上你认为适当的一个条件即可)
14.一个直角三角形的木板,三边的平方和3200,则其斜边为 __________________
15.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,垂足为A,B,S△AOM=8cm2,OA=4cm,则MB=___.
16.如图,点E在正方形ABCD的边AB上,若EB=2,EC=5,那么正方形ABCD的面积为______________
17.小敏设计了一种挂衣架,在挂衣服的时候可以任意角度收扰两个挂衣杆和,然后套进衣服后松开即可.如图1,衣架杆OA=OB.如图2,若衣架收拢时衣服领口宽AB=22cm,且∠AOB=60°,那么这个衣架杆的长OA=OB=______.
18.七年级某班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=10cm,宽AB=8cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长度为 ___________________.
三、解答题
19.如图所示,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.
(1)作△A1B1C1,使得△A1B1C1,与△ABC关于直线l1对称;
(2)作△A2B2C2,使得△A2B2C2,与△ABC关于直线l2对称;
(3)求△A1B1C1的面积= (直接写出结果).
20.如图,AB∥FC,点E是DF的中点,若AB=20,CF=12,你能求出BD的长吗?说明理由.
21.如图,已知△ABC中,已知 ∠B=75?, ∠C=45?,AD是BC边上的高,AE 是∠BAC的角平分线,求∠DAE的度数.
22.一如图,在△ABC中,AB=41cm,BC=18cm,BC边上的中线AD=40cm.△ABC是等腰三角形吗?为什么?
23.为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路的一侧点处有一村庄,村庄到公路的距离为800米,假使宣讲车周围1000米以内能听到广播宣传,宣讲车在公路上沿方向行驶时:
(1)请问村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?
24.Rt△AB C中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).当t为何值时,△ABP为直角三角形?
25.问题情境:已知Rt△ABC的周长为56,斜边长c=25,求△ABC的面积.
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c= ___,
因为c=25,所以a+b=___,
所以(a+b)2=___,
所以a2+ ___=961
因为a2+b2=c2,
所以c2+2ab=961,
所以 ___+2ab=961,
所以ab= 168(第1步)
所以△ABC的面积=ab=× 168= 84(第2步).
合作探究:
(1)填空:填写题目中横线处的内容.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是 ___(填序号).
①整体思想; ②数形结合思想; ③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为6,斜边长为5,求这个直角三角形的周长.
参考答案
1.D
【分析】
根据轴对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
【详解】
A、不是轴对称图形,故A不符合题意;
B、不是轴对称图形,故B不符合题意;
C、不是轴对称图形,故C不符合题意;
D、是轴对称图形,故D符合题意.
故选D.
【点睛】
本题主要考查轴对称图形的知识点.确定轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.D
【分析】
由题意根据角平分线的性质、线段的垂直平分线的性质、轴对称的性质以及等腰三角形性质,利用排除法进行分析即可.
【详解】
解:A. 角平分线上的点到这个角两条边的距离相等,此选项正确;
B. 线段的垂直平分线上的点到这条线段的两个端点的距离相等,此选项正确;
C. 过圆心的直线都是圆的对称轴,而过圆心的直线有无数条,此选项正确;
D. 等腰三角形的对称轴是顶角的平分线所在的直线而不是底角的平分线所在的直线,此选项不正确.
故选:D.
【点睛】
本题主要考查角平分线的性质、线段的垂直平分线的性质、全等三角形判定以及等腰三角形性质,理解相关的性质是解答本题的关键.
3.B
【分析】
先根据勾股定理的逆定理判断出△ABC的形状,再根据直角三角形的性质进行逐一判断即可.
【详解】
解:∵△ABC中,AB=8,BC=15,AC=17,
∴AB2+BC2=82+152=AC2=172,
∴△ABC是直角三角形,AC为斜边,
∴A、C正确;
∵△ABC是直角三角形,
∴S△ABC=×8×15=60,故D正确;
根据三角形三边关系判断∠A≠60°,故B错误
故选:B
【点睛】
本题考查的是勾股定理的逆定理及直角三角形的性质,根据题意判断出△ABC的形状是解答此题的关键.
4.B
【分析】
认真观察各选项给出的图形,根据轴对称的性质,对称轴垂直平分线对应点的连线进行判断.
【详解】
根据轴对称的性质,结合四个选项,只有B选项中对应点的连线被对称轴MN垂直平分,所以B是符合要求的.
故选:B.
【点睛】
本题考查轴对称的性质;应用对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分解题是正确解答本题的关键.
5.C
【分析】
根据BE=CF,求出BC=EF,根据AAS推出△ABC≌△DEF,根据全等三角形的性质推出对应边相等即可.
【详解】
∵BE=CF,
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS),
∴AC=DF=5(全等三角形对应边相等).
故选C.
【点睛】
本题考查了全等三角形的性质和判定的应用,解此题的关键是推出△ABC≌△DEF,注意:全等三角形的对应边相等.
6.B
【分析】
设出正方形的边长,利用勾股定理,解出AB、CD、EF、GH各自的长度,再由勾股定理的逆定理分别验算,看哪三条边能够成直角三角形.
【详解】
解:设小正方形的边长为1,
则AB2=22+22=8,
CD2=22+42=20,
EF2=12+22=5,
GH2=22+32=13.
因为AB2+EF2=GH2,
所以能构成一个直角三角形三边的线段是AB、EF、GH.
故选:B.
【点睛】
本题考查了勾股定理逆定理的应用;解题的关键是解出AB、CD、EF、GH各自的长度.
7.C
【分析】
根据折叠的性质和矩形的性质得出∠CBA=∠CBA′,∠CAD=90°,根据角平分线的性质得出∠A′BE=∠DBE,求出∠CBE=∠CBA′+∠A′BE=∠ABD,代入求出即可.
【详解】
解:∵将长方形纸片的一角折叠,使顶点A落在点A′处,
∴∠CBA=∠CBA′=∠ABA′,∠CAD=90°,
∵BE是∠A′BD的平分线,
∴∠A′BE=∠DBE=∠A′BD,
∴∠CBE=∠CBA′+∠A′BE
= ∠ABA′+ ∠A′BD
= (∠ABA′+∠A′BD)
= ∠ABD
= ×180°
=90°,
故选:C.
【点睛】
本题考查了矩形的性质,折叠的性质,角平分线定义等知识点,关键是求出∠CBE=∠ABD.
8.B
【分析】
根据图形旋转的性质得AC=A′C,∠ACA′=90°,∠B=∠A′B′C,从而得∠AA′C=45°,结合∠1=20°,即可求解.
【详解】
∵将RtABC绕直角项点C顺时针旋转90°,得到A' B'C,
∴AC=A′C,∠ACA′=90°,∠B=∠A′B′C,
∴∠AA′C=45°,
∵∠1=20°,
∴∠B′A′C=45°-20°=25°,
∴∠A′B′C=90°-25°=65°,
∴∠B=65°.
故选B.
【点睛】
本题主要考查旋转的性质,等腰三角形和直角三角形的性质,掌握等腰三角形和直角三角形的性质定理,是解题的关键.
9.C
【详解】
要使△ABP与△ABC全等,必须使点P到AB的距离等于点C到AB的距离,即3个单位长度,所以点P的位置可以是P1,P2,P4三个,故选C.
10.B
【分析】
根据两个正方形的面积求得AB与BD的长度,根据勾股定理求得直角三角形中AD的长度,从而根据圆的面积公式求得半圆的面积.
【详解】
由题意可得,BD=6,AB=10,
则在直角三角形ABC中,AD=8,
则以AD为直径的半圆的面积为:.
故选B
【点睛】
本题考查了正方形与勾股定理的综合运用,利用正方形的面积求出AB与BD的长度是解题的关键.
11.C
【分析】
根据DE是线段AB的垂直平分线,得到BD=AD,便可求解.
【详解】
解:DE是线段AB的垂直平分线
∴BD=AD
∵BD+CD=2020
∴AD+CD=2020 即AC=2020
∵AB=AC
∴AB=2020
故选C.
【点睛】
本题考查等腰三角形性质,以及线段垂直平分线性质,属于基础题.
12.B
【分析】
把立体几何图展开得到平面几何图,如图,然后利用勾股定理计算AB,则根据两点之间线段最短得到蚂蚁所走的最短路线长度.
【详解】
解:展开图为:
则AC=100cm,BC=15×3+10×3=75cm,
在Rt△ABC中,AC=100cm,∴AB==125cm.
所以蚂蚁所走的最短路线长度为125cm.
故选:B.
【点睛】
本题考查了勾股定理的应用,把立体几何图中的问题转化为平面几何图中的问题是解题的关键.
13.或或
【分析】
由∠1=∠2可得∠AEB=∠AEC,AD为公共边,根据全等三角形的判定添加条件即可.
【详解】
∵∠1=∠2,
∴∠AEB=∠AEC,
∵AE为公共边,
∴根据“SAS”得到三角形全等,可添加BE=CE;根据“AAS”可添加∠B=∠C;根据“ASA”可添加∠BAE=∠CAE;
故答案为:BE=CE或∠B=∠C或∠BAE=∠CAE.
【点睛】
本题考查全等三角形的判定,全等三角形的常用的判定方法有SSS、SAS、AAS、ASA、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.熟练掌握全等三角形的判定定理是解题的关键.
14.40
【分析】
设这个直角三角形木板的两直角边长为a、b,斜边为c,然后根据勾股定理及题意可进行求解.
【详解】
解:设这个直角三角形木板的两直角边长为a、b,斜边为c,根据题意得:
,
∴,
∴;
故答案为40.
【点睛】
本题主要考查勾股定理,熟练掌握勾股定理是解题的关键.
15.4cm
【分析】
根据求得AM的长度,利用角平分线上的点到角两边的距离相等即可求解.
【详解】
解:,
解得,
∵OM平分∠POQ,
∴,
故答案为:4cm.
【点睛】
本题考查角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键.
16.21
【分析】
先根据正方形的性质得出∠B=90°,然后在Rt△BCE中,利用勾股定理得出BC2,即可得出正方形的面积.
【详解】
解:∵四边形ABCD是正方形,
∴∠B=90°,
∴BC2=EC2-EB2=52-22=21,
∴正方形ABCD的面积=BC2=21.
故答案为:21.
【点睛】
本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.即如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.也考查了正方形的性质.
17.22
【分析】
图一、图二∠AOB的度数发生变化,但是OA、OB的长度没有改变,在通过∠AOB=60°,OA=OB,得到三角形AOB为等边三角形求解.
【详解】
图一、图二∠AOB的度数发生变化,但是OA、OB的长度没有改变,任然有OA=OB.
∵OA=OB,∠AOB=60°,
∴△AOB为等边三角形,
∴OA=OB=AB=22cm.
【点睛】
本题比较简单,主要是对三角形中等腰、等边三角形的考查,熟练掌握这块的基础知识是解答本题的关键.
18.3cm
【分析】
根据矩形的性质和翻折的性质可得AF=AD=10cm,EF=DE,设EC=xcm,则DE=(8-x)cm,在Rt△ABF中,由勾股定理可得BF的长,继而求得CF的长,在Rt△EFC中,由勾股定理可得关于x的一元二次方程,解方程即可.
【详解】
解:∵四边形ABCD是矩形,BC=10cm,AB=8cm
∴∠B=∠C=90°,AB=CD=8cm,BC=AD=10cm,
根据翻折的性质可得AF=AD=10cm,EF=DE,
设EC=xcm,则EF=DE=(8-x)cm,
在Rt△ABF中,由勾股定理可得: BF
BF,
∴CF=BC-BF=10-6=4cm,
在Rt△EFC中,由勾股定理可得:
即.
解得:
即:EC=3cm
故答案为:3cm
【点睛】
本题主要考查矩形的性质、翻折的性质、勾股定理的应用,解题的关键是根据勾股定理列出.
19.(1)见解析;(2)见解析;(3)4
【分析】
(1)根据轴对称图形的性质进行作图即可;
(2)根据轴对称图形的性质进行作图即可;
(3)利用割补法求解即可.
【详解】
(1)如图,△A1B1C1与△ABC关于直线l1对称;
(2)如图,△A2B2C2与△ABC关于直线l2对称;
(3).
【点睛】
本题考查了轴对称作图及三角形面积的求解,能够准确根据题目要求作出对称图形,及熟练运用割补法求解三角形面积是解决问题的关键.
20.8,理由见解析
【分析】
由题意易得DE=FE,∠A=∠ECF,∠ADE=∠F,进而可证△ADE≌△CFE,则有CF=AD,然后问题可求解.
【详解】
解:BD=8,理由如下:
∵AB∥FC,
∴∠A=∠ECF,∠ADE=∠F,
∵点E是DF的中点,
∴DE=FE,
∴△ADE≌△CFE(AAS),
∴CF=AD,
∵AB=20,CF=12,
∴.
【点睛】
本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
21.15?
【分析】
由三角形的内角和定理,可求∠BAC=60°,又由AE是∠BAC的平分线,可求∠BAE=30°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=15°,所以∠DAE=∠BAE-∠BAD=15°.
【详解】
解:∵ ∠B=75? ,∠C=45?
∴∠BAC=60?
∵ AE是∠BAC的角平分线
∴∠BAE=∠BAC=30?
∵ AD是BC边上的角高
∴∠BAD=90?-∠B=90?-75?=15?
∴∠DAE=∠BAE-∠BAD=30?-15?=15?
【点睛】
本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和180°.
22.△ABC是等腰三角形,理由见解析.
【分析】
由已知可得BD的长,再根据勾股定理的逆定理可判定AD垂直BC,从而可利用勾股定理求得AC的长,此时发现AB=AC,即该三角形是等腰三角形.
【详解】
解:△ABC是等腰三角形,理由如下:
∵BC=18cm,BC边上的中线为AD,
∴BD=CD=9cm.
∵AB=41cm,BD=9cm,AD=40cm,
∴AB2=1681,BD2+AD2=1681,
∴AB2=BD2+AD2,
∴AD⊥BC.
∵BD=CD,
∴AC=AB,
∴△ABC是等腰三角形.
23.(1)村庄能听到宣传. 理由见解析;(2)村庄总共能听到4分钟的宣传.
【分析】
(1)根据题意村庄A到公路MN的距离为800米<1000米,即可解答
(2)假设当宣讲车行驶到P点开始影响村庄,行驶Q点结束对村庄的影响
【详解】
解:(1)村庄能听到宣传.
理由:因为村庄A到公路MN的距离为800米<1000米,所以村庄能听到宣传
(2)如图,假设当宣讲车行驶到P点开始影响村庄,行驶Q点结束对村庄的影响,利用勾股定理进行计算即可解答
则AP=AQ=1000米,AB=800米.
∴BP=BQ==600米.
∴PQ=1200米.
、∴影响村庄的时间为:1200÷300=4(分钟).
∴村庄总共能听到4分钟的宣传.
【点睛】
此题考查解直角三角形,利用勾股定理进行计算是解题关键
24.4或12.5
【分析】
分当∠AP1B=90°,△ABP1为直角三角形时和当∠BAP2=90°,△ABP2为直角三角形时两种情况讨论即可.
【详解】
解:在Rt△ABC中,由勾股定理得:
BC2+AC2=AB2
∴BC2+62=102
∴BC=8,
当∠AP1B=90°,△ABP1为直角三角形时,P1在C处,即BP1=8,
∴8÷2=4(s);
当∠BAP2=90°,△ABP2为直角三角形时,
设BP2为x,则CP2=x-8
在△ACP2中,由勾股定理得:
AC2+CP22=AP22
∴62+(x-8)2=AP22
在△BAP2中,由勾股定理得:
AB2+AP22=BP22
∴AP22= BP22- AB2=x2-102
∴x2-102=62+(x-8)2
∴x=12.5.
【点睛】
本题考查了勾股定理,解答本题的关键是掌握勾股定理的应用.
25.(1)56,31,961,2ab+b2,625;(2)①;(3)12
【分析】
(1)根据三角形的周长定义,勾股定理,三角形的面积公式即可求解;
(2)根据(1)的解答过程得到由第1步到第2步体现出来的数学思想;
(3)设直角三角形的两直角边分别是a、b(a<b,且a、b均为正数).利用勾股定理和三角形的面积公式求得两直角边是6和8.然后由三角形的周长公式求得该直角三角形的周长.
【详解】
解:(1)∵Rt△ABC的周长为56,
∴a+b+c=56,
∵c=25,
∴a+b=31,
∴(a+b)2=961,
∴a2+2ab+b2=961
∵a2+b2=c2,
∴c2+2ab=961,
∴625+2ab=961,
∴ab= 168(第1步)
∴△ABC的面积=ab=× 168= 84(第2步).
故答案为:①56 ②31 ③961(填312也可以) ④2ab+b2 ⑤625
(2)∵由第1步到第2步中用了整体代入,
∴体现的数学思想是①.
故答案为①.
(3)设直角三角形的两直角边分别是a、b, 斜边为c
∵三角形面积为6
∴ab=6,
∴2ab=24
∵a2+b2=c2
∴a2+2ab+b2=52 +2ab
∴(a+b)2=25+24=49
∵a+b?0
∴ a+b=7
所以这个直角三角形的周长是:a+b+c=7+5=12.
【点睛】
本题主要考查了利用三角形的面积公式寻找相等关系,同时也考查了勾股定理的内容.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.
同课章节目录
