2021普通高等学校招生全国统一考试·信息卷(Word含解析)
文档属性
| 名称 | 2021普通高等学校招生全国统一考试·信息卷(Word含解析) | 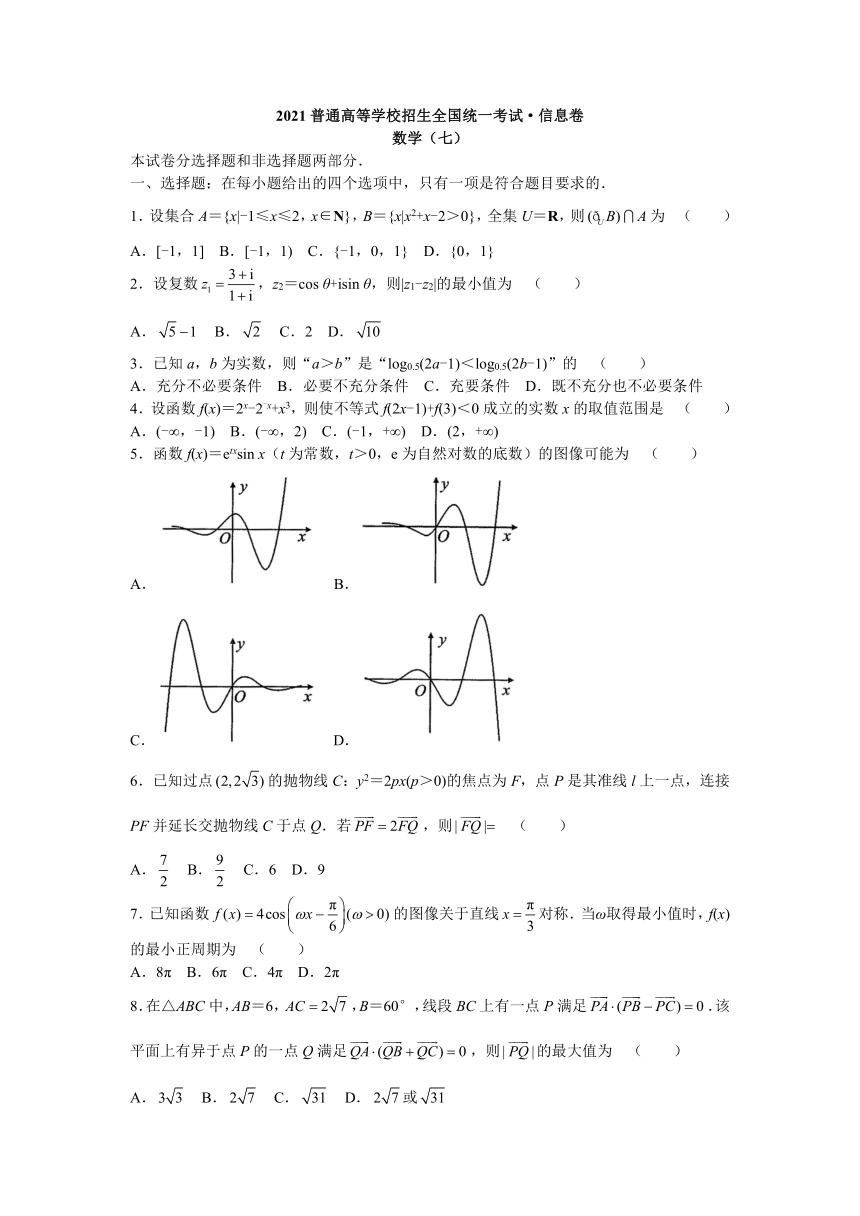 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 19:02:12 | ||
图片预览





文档简介
2021普通高等学校招生全国统一考试·信息卷
数学(七)
本试卷分选择题和非选择题两部分.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={x|-1≤x≤2,x∈N},B={x|x2+x-2>0},全集U=R,则为
(
)
A.[-1,1]
B.[-1,1)
C.{-1,0,1}
D.{0,1}
2.设复数,z2=cos
θ+isin
θ,则|z1-z2|的最小值为
(
)
A.
B.
C.2
D.
3.已知a,b为实数,则“a>b”是“log0.5(2a-1)<log0.5(2b-1)”的
(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.设函数f(x)=2x-2-x+x3,则使不等式f(2x-1)+f(3)<0成立的实数x的取值范围是
(
)
A.(-∞,-1)
B.(-∞,2)
C.(-1,+∞)
D.(2,+∞)
5.函数f(x)=etxsin
x(t为常数,t>0,e为自然对数的底数)的图像可能为
(
)
A.
B.
C.
D.
6.已知过点的抛物线C:y2=2px(p>0)的焦点为F,点P是其准线l上一点,连接PF并延长交抛物线C于点Q.若,则
(
)
A.
B.
C.6
D.9
7.已知函数的图像关于直线对称.当ω取得最小值时,f(x)的最小正周期为
(
)
A.8π
B.6π
C.4π
D.2π
8.在△ABC中,AB=6,,B=60°,线段BC上有一点P满足.该平面上有异于点P的一点Q满足,则的最大值为
(
)
A.
B.
C.
D.或
二、选择题:在每小题给出的选项中,有多项符合题目要求.
9.有一位生态学家曾经做过这样一个实验:在0.5
mL培养液中放入5只草履虫,然后每隔24
h统计一次草履虫的数量,得到了如下表的统计数据:
x(时间/天)
0
1
2
3
4
y(草履虫数/只)
5
30
121
329
375
甲、乙两位同学根据这些数据,分别构建了y关于x的两个回归方程,并计算得各自的相关系数:
,r1=0.9626;,r2=0.9583.
则以下说法不正确的是
(
)
A.甲同学构建的回归方程说明y与x呈负相关关系
B.乙同学构建的回归方程的图像过样本中心点(2,172)
C.按乙同学构建的回归方程估计,10
h后的草履虫数在2522只附近的可能性比较大
D.两位同学所构建的回归方程描述x和y之间的相关关系效果都很好
10.函数f(x)是定义在R上的奇函数,且在(-2,2)上单调递增,g(x)=f(x-2)也是奇函数,则
(
)
A.函数f(x)是周期为4的周期函数
B.函数g(x)是周期为2的周期函数
C.函数f(x)的图像关于点(4,0)对称
D.g(2),,g(5)的大小关系为
11.在三棱柱ABC-A1B1C1中,点M为棱AB的中点,点N是侧面ACC1A1内(含边界)一动点,且MN∥平面BCC1B1,则下列四个结论一定正确的是
(
)
A.直线MN与CC1是异面直线
B.点N的轨迹是一条线段,其长度等于侧棱长
C.MN⊥平面ACC1A1
D.由点N的轨迹和点M确定的平面垂直于底面ABC
12.若数列{an}满足:?A,B∈R,AB≠0,使得对于?n∈N
,都有an+2=Aan+1+Ban,则称{an}具有“三项相关性”.下列说法正确的有
(
)
A.若数列{an}是等差数列,则{an}具有“三项相关性”
B.若数列{an}是等比数列,则{an}具有“三项相关性”
C.若数列{an}是周期数列,则{an}具有“三项相关性”
D.已知数列{an}具有“三项相关性”,且正数A,B满足A+1=B,a1+a2=B.设数列{bn}的通项公式为bn=Bn,{an}与{bn}的前n项和分别为Sn,Tn,则对于?n∈N
,2S2n<T2n恒成立
三、填空题
13.已知α为第三象限角,且,则tan
α的值为________.
14.甲、乙、丙、丁、戊、己六名同学进行劳动技术比赛,决出第一名到第六名的名次.甲、乙两名参赛者去询问他们的成绩,回答者对甲说:“很遗憾,你们都没有获得冠军.”对乙说:“你当然不会是最差的.”则六人的名次排列的可能情况数为________.
15.在高为1的正四面体PABC中,P在底面ABC上的射影为P′,作平行于平面ABC的平面,分别交线段PA,PB,PC于点A′,B′,C′.当三棱锥P′-A′B′C′的体积最大时,三棱锥P′-A′B′C′的外接球的表面积为________.
16.已知双曲线C:的左、右焦点分别为F1,F2,其一条渐近线的方程为,点M是其右支上一点,点N是圆E:x2+y2-8y+15=0上的点.若|MF1|+|MN|的最小值为8,则此时双曲线C的实轴长为________.
四、解答题:解答应写出文字说明、证明过程或演算步骤.
17.在①bn=λan,②,③bn=λ+an这三个条件中任选一个,补充在下面的问题中.若问题中的t存在,求出t的值;若t不存在,请说明理由.
问题:设等差数列{an}的前n项和为Sn,a2=3,a5=S3,数列{bn}满足_________.对于任意的λ(λ≠0),是否存在正整数t使得b1,b3,bt成等比数列?
注:如果选择多个条件分别解答,那么按第一个解答计分.
18.在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,△ABC的外接圆半径为R.已知,且a<b.
(1)求C.
(2)若R=2,求AB边上的中线的取值范围.
19.如图,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PAB,△PAD均是以A为顶角的等腰直角三角形,M为PD的中点.
(1)证明:PB∥平面ACM.
(2)求PM与平面ACM所成角的正弦值.
20.由商务部和北京市人民政府共同举办的2020年中国国际服务贸易交易会(简称服贸会)于9月4日开幕,主题为“全球服务,互惠共享”.某高校为了调查学生对服贸会的了解情况,决定随机抽取100名学生进行采访.根据统计结果,采访的学生中男女比例为3:2,已知抽取的男生中有10名不了解服贸会,抽取的女生中有25名了解服贸会,请你解答下面所提出的相关问题.
(1)完成2×2列联表,并回答“是否有99%的把握认为学生对服贸会的了解情况与性别有关”.
了解情况性别
了解
不了解
合计
男生
女生
合计
100
(2)若从被采访的学生中利用分层抽样的方法抽取5人,再从这5人中随机抽取3人在校内开展一次“介绍服贸会”的专题活动,记抽取男生的人数为ξ,求出ξ的分布列及数学期望.
附:,n=a+b+c+d.
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
21.已知椭圆C:的左、上顶点分别为B,A,直线l∥AB,与椭圆C交于P,Q两点.
(1)求PQ中点M的轨迹方程.
(2)设椭圆C的左、右焦点分别为F1,F2,证明为定值,并求此定值.
22.已知函数有两个极值点,分别为x1,x2.
(1)求a的取值范围.
(2)证明:(其中e为自然对数的底数).
参考答案
7
2021普通高等学校招生全国统一考试·信息卷
数学(七)
一、1.D
【命题意图】本题考查一元二次不等式的解法,集合的补集、交集,体现了数学运算的核心素养.
【解析】∵A={0,1,2},,∴.故选D.
2.A
【命题意图】本题考查复数的除法运算、复数的几何意义,考查数形结合思想、转化与化归思想,体现了数学运算、直观想象等核心素养.
多法解题
方法一
.由复数的几何意义可知在复平面内,复数z2对应的点的轨迹是以原点为圆心的单位圆.如图,z1对应的向量为,z2对应的向量为,则.∴当B取单位圆与OA的交点时,有最小值,为.故选A.
方法二
z1=2-i.由复数的几何意义可知在复平面内,复数z1对应的向量,z2对应的向量,则
,其中,.当sin(θ-φ)=-1时,|z1-z2|取得最小值,为.故选A.
方法总结
关于两个复数之差的模的最值问题,可结合复数的几何意义,将其转化为向量的模的问题.求向量之差的模的最值,有两种方法:(1)几何法,将复数z2在复平面内对应的向量与单位圆联系起来,通过向量的运算求其最值;(2)代数法,利用,通过向量的数量积运算,构造关于θ的三角函数,利用其性质求最值.
3.B
【命题意图】本题考查不等式的性质,对数函数的单调性,充分条件、必要条件的判断,体现了数学运算、逻辑推理等核心素养.
【解析】.故“a>b”是“log0.5(2a-1)<log0.5(2b-1)”的必要不充分条件.故选B.
4.A
【命题意图】本题考查函数的单调性、奇偶性,利用函数的单调性解不等式,考查转化与化归思想,体现了数学运算、逻辑推理等核心素养.
【解析】由函数解析式可知,函数f(x)是定义在R上的奇函数,且单调递增,于是原不等式可化为f(2x-1)<-f(3)=f(-3),所以2x-1<-3,解得x<-1.故选A.
方法总结
用常规方法解答与函数的奇偶性、单调性有关的不等式问题,需要将不等式转化为f(g(x))≤f(h(x))的形式,再利用函数的单调性“脱去”最外层函数,转化为一般不等式.
名师评题
解本题时要撇开函数解析式的表象,抓住函数隐含的性质,如奇偶性和单调性(本题所给的函数既是奇函数又是增函数),然后利用性质巧妙解题,能很好地考查学生的数学功底和数学素养.本题如果解题方法选择不当,会耗时过多且容易出错.
5.B
【命题意图】本题考查函数图像的识别,体现了直观想象、逻辑推理等核心素养.
【解析】当x=0时,f(x)=0,排除A.
当0<x<π时,f(x)>0,排除D.
因为t>0,所以et>1.根据指数函数的性质,对于x0>0,.又因为|sin
x0|=|sin(-x0)|,所以|f(x0)|>|f(-x0)|,排除C.故选B.
6.B
【命题意图】本题考查抛物线的方程及其简单的几何性质、向量的数乘,体现了数学运算、直观想象等核心素养.
【解析】将点的坐标代入y2=2px(p>0),解得p=3,即抛物线C的方程为y2=6x.设准线l与x轴交于点A,则|AF|=3.过点Q作QQ1⊥l于点Q1,则|QQ1|=|FQ|.因为AF∥QQ1,,所以,所以,即.故选B.
7.C
【命题意图】本题考查三角函数的图像与性质,体现了逻辑推理、数学运算等核心素养.
【解析】由题意可知当时,取得最大值或最小值,所以
,k∈Z,所以,k∈Z.因为ω>0,所以当k=0时,ω取得最小值,此时f(x)的最小正周期.故选C.
8.B
【命题意图】本题考查平面向量的数量积、向量模的最大值、余弦定理的应用,考查数形结合思想、转化与化归思想,体现了数学运算、逻辑推理等核心素养.
【解析】由,得,∴PA⊥BC.又∵点P在线段BC上,∴△ABC为锐角三角形.设BC=x(x>3),则由余弦定理,得,解得x=4或x=2(舍去).如图,设BC的中点为H,连接AH,QH,则
,∴点Q在以AH为直径的圆上,如图,作出该圆.又∵AP⊥HP,∴点P也在以AH为直径的圆上,∴的最大值为该圆的直径,即AH.由余弦定理,得
,∴的最大值为.故选B.
二、9.ABC
【命题意图】本题考查回归方程、相关系数,体现了数学运算、数据分析等核心素养.
【解析】由r1>0或散点图(图略)可以得出y与x不呈负相关关系,A不正确.
是非线性回归方程,它的图像过样本中心点(6,172),B不正确.
注意表格中时间的单位是天而不是时(h),不能直接将x=10代入求解,C不正确.
这两个回归方程的相关系数均大于0.75,所以用这两个回归模型描述x和y之间的相关关系都有很好的效果,D正确.故选ABC.
10.ACD
【命题意图】本题考查函数的奇偶性、单调性、周期性,函数图像的对称性,体现了数学运算、逻辑推理等核心素养.
【解析】由题意得f(-x)=-f(x),g(-x)=-g(x).又g(x)=f(x-2),所以f(-x-2)=-f(x-2),即f(x+2)=f(x-2),所以函数f(x)是周期为4的周期函数,故A正确.因为f(x)的图像关于点(0,0)对称,周期为4,所以函数f(x)的图像关于点(4,0)对称,故C正确.由g(x)=f(x-2),得g(x+4)=f(x+2)=f(x+2-4)=f(x-2)=g(x),即函数g(x)是周期为4的周期函数,故B错误.由g(2)=f(2-2)=f(0),,g(5)=f(5-2)=f(3)=f(-1),且f(x)在(-2,2)上单调递增,得,所以,故D正确.选ACD.
11.AB
【命题意图】本题考查线线、线面、面面之间的位置关系,考查转化与化归思想,体现了逻辑推理、直观想象等核心素养.
【解析】如图,分别取棱AC,A1C1的中点D,E,连接DE,DM,ME,则DE∥CC1,DM∥BC.又DE∩DM=D,DE?平面MDE,DM?平面MDE,CC1?平面BCC1B1,BC?平面BCC1B1,所以平面MDE∥平面BCC1B1.要使MN∥平面BCC1B1,只需MN?平面MDE.又点N在侧面ACC1A1内(含边界),所以点N的轨迹就是线段DE,其长度等于侧棱长,故B正确.
易得直线MN与CC1是异面直线,故A正确.
因为不知道三棱柱ABC-A1B1C1是否为直三棱柱,且并不知其底面三角形ABC的具体形状,无法判断C,D是否正确.故选AB.
易错警示
棱柱上、下底面相互平行,侧面为平行四边形,故其侧面不一定垂直于底面.而直棱柱的侧面都垂直于底面,需注意区分.
12.ABD
【命题意图】本题考查与数列有关的新定义问题,考查转化与化归思想,体现了数学运算、逻辑推理等核心素养.
【解析】若{an}为等差数列,则an+2+an=2an+1,∴取A=2,B=-1即可,故A正确.
若{an}为等比数列,设公比为q,则由an+2=Aan+1+Ban,得anq2=Aq·an+Ban,则Aq+B=q2,∴对任意一个确定的等比数列{an},任取满足上述二元一次方程的A,B(AB≠0)均可,故B正确.
任取一周期大于2的周期数列(如1,2,3,1,2,3,…),易得A,B不存在,故C错误.
将A=B-1代入an+2=Aan+1+Ban,得an+2=(B-1)an+1+Ban,即an+2+an+1=B(an+1+an),∴.而,∴.∵A=B-1>0,∴B>1,∴,∴2S2n<T2n,故D正确.选ABD.
名师评题
本题设问新颖,具有一定的创新性.前3个选项熟悉而不俗套,以3个基本数列为背景,考查学生对概念、性质的深刻理解以及灵活运用的能力.第4个选项在计算S2n时要用到“并项法”,考查学生的灵活应变能力和创新能力,对计算方法和计算能力有着较高的要求,符合高考对运算能力的考查要求,不是进行繁难的运算,而是通过增加思维考核的深度,使学生去想怎么算,关键是“想”而不是“算”.
三、13.2
【命题意图】本题考查同角三角函数的基本关系、二倍角公式,体现了数学运算、逻辑推理等核心素养.
【解析】由,得,所以,于是
,解得tan
α=±2.又因为α是第三象限角,所以tan
α=2.
14.384
【命题意图】本题考查排列知识,体现了数学运算、逻辑推理等核心素养.
【解析】先排乙,有4个位置(不能排第一和第六的位置),再排甲,有4个位置(不能排乙所在的位置和第一的位置),剩下的四名同学随意排.故可能的情况数为.
技巧点拨
解本题的关键是注意“你们都没有获得冠军”这一条件,以及排甲、乙位置的顺序.
15.π
【命题意图】本题考查三棱锥及三棱锥的外接球的表面积,体现了数学运算、逻辑推理、直观想象等核心素养.
【解析】如图(1),设PP′与平面A′B′C′交于点H,则P′H为三棱锥P′-A′B′C′的高.由题意知PP′=1.设P′H=a(0<a<1),则△A′B′C′与△ABC的相似比为1-a,∴两者面积之比为(1-a)2.∴
,当且仅当2a=1-a,即时,取等号.易知,正四面体PABC的棱长为,∴当三棱锥P′-A′B′C′的体积最大时,正三角形A′B′C′的边长为.连接C′H,易知.设三棱锥P′-A′B′C′的外界球半径为r,球心为O,如图(2),取截面P′C′H分析.易知点O在直线P′H上,连接OC′,则,解得,∴三棱锥P′-A′B′C′的外接球的表面积S=4πr2=π.
方法总结
此类题目应分两步,首先确定三棱锥的体积何时最大,之后通过几何关系求出其外接球的半径.在求三棱锥体积函数V(a)的最值时,可利用基本不等式(需要巧妙地“凑”),也可求函数的导数,进而求出其体积最大时a的值.在求该三棱锥的外接球的半径时,需充分挖掘其几何关系,构造出直角三角形,利用勾股定理,建立关于r的方程.
知识拓展
在边长为a的正四面体PABC中,顶点P在底面正三角形ABC上的射影P′即为△ABC的重心(三边中线的交点),AP在底面上的射影AP′的长度为,正四面体的高PP′的长度为.掌握这些比例关系,可大大提高解题效率.
16.4
【命题意图】本题考查双曲线的定义、渐近线,圆的方程,直线与圆的位置关系,线段和的最值问题,考查转化与化归思想、数形结合思想,体现了数学运算、逻辑推理、直观想象等核心素养.
【解析】连接MF2,根据双曲线的定义,可知|MF1|=|MF2|+2a.圆E的标准方程为x2+(y-4)2=1,圆心E(0,4),半径为1,圆心E到直线,即的距离
,故该圆与双曲线的渐近线相离.于是|MF1|+|MN|=|MF2|+2a+|MN|≥|MF2|+2a+|ME|-1≥|EF2|+2a-1,所以当E,M,F2三点共线时,|MF1|+|MN|取到最小值,最小值为|EF2|+2a-1.由双曲线的渐近线方程为,不妨设a=2m(m>0),则,c=3m,所以
,所以,解得m=1,于是a=2,所以实轴长2a=4.
名师评题
高考对解析几何的考查十分注重对圆锥曲线的定义及性质的考查.本题考查了双曲线的定义、圆的性质以及平面几何中的最短距离问题,重点考查学生灵活运用定义和平面几何知识解决问题的能力.“解过无数问题,其实都是转化.”本题就是要把焦半径|MF1|转化到焦半径|MF2|,把点M到圆上动点的距离转化为到圆心(定点)的距离,很好地考查了学生的逻辑推理、直观想象、数学运算等核心素养.
四、17.【命题意图】本题考查等差数列、等比数列的性质,体现了逻辑推理、数学运算等核心素养.
【解】设等差数列{an}的公差为d,
则
整理,得解得
所以an=a1+(n-1)d=1+(n-1)×2=2n-1.
方案一:选条件①.
假设数列{bn}中存在某项bt使得b1,b3,bt成等比数列,则,即(λa3)2=λa1·λat.
因为λ≠0,所以.
又因为a3=2×3-1=5,a1=2×1-1=1,at=2t-1,
所以52=1·(2t-1),解得t=13.
所以存在正整数t=13使得b1,b3,bt成等比数列.
方案二:选条件②.
假设数列{bn}中存在某项bt使得b1,b3,bt成等比数列,则,即.
因为λ≠0,所以.
又因为a3=2×3-1=5,a1=2×1-1=1,at=2t-1,
所以52=1·(2t-1),解得t=13.
所以存在正整数t=13使得b1,b3,bt成等比数列.
方案三:选条件③.
假设数列{bn}中存在某项bt使得b1,b3,bt成等比数列,则,即(λ+a3)2=(λ+a1)·(λ+at),
若λ=2,则(2+a3)2=(2+a1)·(2+at),
将a3=2×3-1=5,a1=2×1-1=1,at=2t-1代入并整理,得3t=23,所以.
又t∈N
,所以不存在满足条件的正整数t.
18.【命题意图】本题考查正弦定理、余弦定理的应用,体现了数学运算、逻辑推理等核心素养.
【解】(1)∵,∴,即
,∴,∴.∵a<b,∴A<B,∴,∴.
(2)方法一
由正弦定理,得
,a=2Rsin
A=4sin
A.
设AB的中点为D,则在△BDC中,由余弦定理,得
CD2=BC2+BD2-2BC·BD·cos
B
.
由解得
.∴,∴,∴CD2∈(7,9),∴.∴AB边上的中线的取值范围为.
方法二
以△ABC的外接圆圆心O为坐标原点,建立如图的平面直角坐标系,使x轴与AB平行.
设AB的中点为D,连接OA,OB,OC,CD.
由正弦定理,得
,∴,∴,∴D(0,-1).
设C(2cos
θ,2sin
θ)(θ为射线OC与x轴非负半轴的夹角).
由题意,得
解得.∴.∵,∴7<5+4sin
θ<9,∴,∴AB边上的中线的取值范围为.
19.【命题意图】本题考查线面平行、利用空间向量求线面所成角的正弦值,考查转化与化归思想,体现了数学运算、逻辑推理、直观想象等核心素养.
(1)【证明】如图,连接BD,交AC于点O,连接OM,则O为BD的中点.
又∵M为PD的中点,∴OM为△PBD的中位线,∴OM∥PB.∵OM?平面ACM,PB?平面ACM,∴PB∥平面ACM.
(2)【解】取CP的中点N,连接ON.∵△PAB,△PAD均是以A为顶角的等腰直角三角形,∴PA⊥AB,PA⊥AD.
又∵AB∩AD=A,AB,AD?平面ABCD,∴PA⊥平面ABCD.∵O,N分别为AC,PC的中点,∴ON∥AP,∴ON⊥平面ABCD.
如图,以O为坐标原点,分别以直线OC,OB,ON为x轴、y轴、z轴建立空间直角坐标系O-xyz.
设AP=AB=2.∵∠ABC=60°,∴△ABC为等边三角形,∴OC=1,,,∴C(1,0,0),P(-1,0,2),.∴,,
.
设平面ACM的法向量为.
由得
令y=2,则.∴.
设PM与平面ACM所成的角为θ,与所成的角为α,则.∴PM与平面ACM所成角的正弦值为.
20.【命题意图】本题考查独立性检验、离散型随机变量的分布列及期望,体现了数学运算、数据分析等核心素养.
【解】(1)2×2列联表如下:
了解情况性别
了解
不了解
合计
男生
50
10
60
女生
25
15
40
合计
75
25
100
,∴没有99%的把握认为学生对服贸会的了解情况与性别有关.
(2)根据题意,抽取的5人中男生有3人,女生有2人.
从这5人中随机抽取3人,则男生人数ξ的所有可能取值为1,2,3,
则,
,
.∴ξ的分布列为
ξ
1
2
3
P
∴.
21.【命题意图】本题考查直线与椭圆的位置关系、轨迹方程的求解、向量数量积的坐标表示,体现了数学运算、直观想象、逻辑推理等核心素养.
【解】(1)由,得a=2,b=1.
设P(x1,y1),Q(x2,y2),则,且
①-②,得.
化简,得,∴,∴直线OM的方程为.
将代入椭圆C的方程,得.解得.∵点M的轨迹在椭圆C内,∴点M的轨迹方程为.
(2)设l:.
将代入椭圆方程并化简,得x2+2mx+2m2-2=0.
当Δ=4m2-4(2m2-2)=4(2-m2)>0时,
有
又∵,,∴
.∴为定值,且定值为-1.
方法总结
设而不求是指在解题过程中根据需要设出变量,但并不直接求出其具体值,而是利用某种关系(如和、差、积)来表示变量之间的关系.在解决圆锥曲线的有关问题时,能够达到“化难为易、化繁为简”的效果.
22.【命题意图】本题考查函数的极值问题、构造函数解答不等式的证明问题,考查转化与化归思想、方程思想,体现了数学运算、逻辑推理等核心素养.
(1)【解】由题意,得f(x)的定义域为(0,+∞).
.
由f(x)在其定义域内有两个极值点,可得方程f′(x)=0在x>0时有两个不相等的实数根,
即方程在x>0时有两个不相等的实数根.
设,则
.
令g′(x)=0,得,∴当时,g(x)单调递减;当时,g(x)单调递增.∴.
又∵当x→0时,g(x)→+∞;当x→+∞时,g(x)→0,∴.
综上可知,a的取值范围为.
(2)【证明】由题意,知∴
.∴要证,即证,即证x1x2>e.
不妨设,则即证.∵,g(x)在上单调递减,∴即证.
又∵g(x1)=g(x2)=a,∴即证,即证
,即证.
设,即证.
设
,
则,∴h(x)在[e2,+∞)上为增函数,∴.
综上可知,成立.
名师评题
导数题作为高考压轴题都有一定难度,对学生思维的深度有较高要求,学生除掌握必要的基础知识外,还需要有较强的观察力、想象力、应变力和逻辑推理能力.本题第(1)问比较常规,第(2)问除考查了分析法、消元法、换元法,方程思想、转化与划归思想,解法“简约而不简单”,需要步步为营、层层深入、随机应变,考查学生的数学素养,有着较高的区分度.
数学(七)
本试卷分选择题和非选择题两部分.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={x|-1≤x≤2,x∈N},B={x|x2+x-2>0},全集U=R,则为
(
)
A.[-1,1]
B.[-1,1)
C.{-1,0,1}
D.{0,1}
2.设复数,z2=cos
θ+isin
θ,则|z1-z2|的最小值为
(
)
A.
B.
C.2
D.
3.已知a,b为实数,则“a>b”是“log0.5(2a-1)<log0.5(2b-1)”的
(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.设函数f(x)=2x-2-x+x3,则使不等式f(2x-1)+f(3)<0成立的实数x的取值范围是
(
)
A.(-∞,-1)
B.(-∞,2)
C.(-1,+∞)
D.(2,+∞)
5.函数f(x)=etxsin
x(t为常数,t>0,e为自然对数的底数)的图像可能为
(
)
A.
B.
C.
D.
6.已知过点的抛物线C:y2=2px(p>0)的焦点为F,点P是其准线l上一点,连接PF并延长交抛物线C于点Q.若,则
(
)
A.
B.
C.6
D.9
7.已知函数的图像关于直线对称.当ω取得最小值时,f(x)的最小正周期为
(
)
A.8π
B.6π
C.4π
D.2π
8.在△ABC中,AB=6,,B=60°,线段BC上有一点P满足.该平面上有异于点P的一点Q满足,则的最大值为
(
)
A.
B.
C.
D.或
二、选择题:在每小题给出的选项中,有多项符合题目要求.
9.有一位生态学家曾经做过这样一个实验:在0.5
mL培养液中放入5只草履虫,然后每隔24
h统计一次草履虫的数量,得到了如下表的统计数据:
x(时间/天)
0
1
2
3
4
y(草履虫数/只)
5
30
121
329
375
甲、乙两位同学根据这些数据,分别构建了y关于x的两个回归方程,并计算得各自的相关系数:
,r1=0.9626;,r2=0.9583.
则以下说法不正确的是
(
)
A.甲同学构建的回归方程说明y与x呈负相关关系
B.乙同学构建的回归方程的图像过样本中心点(2,172)
C.按乙同学构建的回归方程估计,10
h后的草履虫数在2522只附近的可能性比较大
D.两位同学所构建的回归方程描述x和y之间的相关关系效果都很好
10.函数f(x)是定义在R上的奇函数,且在(-2,2)上单调递增,g(x)=f(x-2)也是奇函数,则
(
)
A.函数f(x)是周期为4的周期函数
B.函数g(x)是周期为2的周期函数
C.函数f(x)的图像关于点(4,0)对称
D.g(2),,g(5)的大小关系为
11.在三棱柱ABC-A1B1C1中,点M为棱AB的中点,点N是侧面ACC1A1内(含边界)一动点,且MN∥平面BCC1B1,则下列四个结论一定正确的是
(
)
A.直线MN与CC1是异面直线
B.点N的轨迹是一条线段,其长度等于侧棱长
C.MN⊥平面ACC1A1
D.由点N的轨迹和点M确定的平面垂直于底面ABC
12.若数列{an}满足:?A,B∈R,AB≠0,使得对于?n∈N
,都有an+2=Aan+1+Ban,则称{an}具有“三项相关性”.下列说法正确的有
(
)
A.若数列{an}是等差数列,则{an}具有“三项相关性”
B.若数列{an}是等比数列,则{an}具有“三项相关性”
C.若数列{an}是周期数列,则{an}具有“三项相关性”
D.已知数列{an}具有“三项相关性”,且正数A,B满足A+1=B,a1+a2=B.设数列{bn}的通项公式为bn=Bn,{an}与{bn}的前n项和分别为Sn,Tn,则对于?n∈N
,2S2n<T2n恒成立
三、填空题
13.已知α为第三象限角,且,则tan
α的值为________.
14.甲、乙、丙、丁、戊、己六名同学进行劳动技术比赛,决出第一名到第六名的名次.甲、乙两名参赛者去询问他们的成绩,回答者对甲说:“很遗憾,你们都没有获得冠军.”对乙说:“你当然不会是最差的.”则六人的名次排列的可能情况数为________.
15.在高为1的正四面体PABC中,P在底面ABC上的射影为P′,作平行于平面ABC的平面,分别交线段PA,PB,PC于点A′,B′,C′.当三棱锥P′-A′B′C′的体积最大时,三棱锥P′-A′B′C′的外接球的表面积为________.
16.已知双曲线C:的左、右焦点分别为F1,F2,其一条渐近线的方程为,点M是其右支上一点,点N是圆E:x2+y2-8y+15=0上的点.若|MF1|+|MN|的最小值为8,则此时双曲线C的实轴长为________.
四、解答题:解答应写出文字说明、证明过程或演算步骤.
17.在①bn=λan,②,③bn=λ+an这三个条件中任选一个,补充在下面的问题中.若问题中的t存在,求出t的值;若t不存在,请说明理由.
问题:设等差数列{an}的前n项和为Sn,a2=3,a5=S3,数列{bn}满足_________.对于任意的λ(λ≠0),是否存在正整数t使得b1,b3,bt成等比数列?
注:如果选择多个条件分别解答,那么按第一个解答计分.
18.在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,△ABC的外接圆半径为R.已知,且a<b.
(1)求C.
(2)若R=2,求AB边上的中线的取值范围.
19.如图,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PAB,△PAD均是以A为顶角的等腰直角三角形,M为PD的中点.
(1)证明:PB∥平面ACM.
(2)求PM与平面ACM所成角的正弦值.
20.由商务部和北京市人民政府共同举办的2020年中国国际服务贸易交易会(简称服贸会)于9月4日开幕,主题为“全球服务,互惠共享”.某高校为了调查学生对服贸会的了解情况,决定随机抽取100名学生进行采访.根据统计结果,采访的学生中男女比例为3:2,已知抽取的男生中有10名不了解服贸会,抽取的女生中有25名了解服贸会,请你解答下面所提出的相关问题.
(1)完成2×2列联表,并回答“是否有99%的把握认为学生对服贸会的了解情况与性别有关”.
了解情况性别
了解
不了解
合计
男生
女生
合计
100
(2)若从被采访的学生中利用分层抽样的方法抽取5人,再从这5人中随机抽取3人在校内开展一次“介绍服贸会”的专题活动,记抽取男生的人数为ξ,求出ξ的分布列及数学期望.
附:,n=a+b+c+d.
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
21.已知椭圆C:的左、上顶点分别为B,A,直线l∥AB,与椭圆C交于P,Q两点.
(1)求PQ中点M的轨迹方程.
(2)设椭圆C的左、右焦点分别为F1,F2,证明为定值,并求此定值.
22.已知函数有两个极值点,分别为x1,x2.
(1)求a的取值范围.
(2)证明:(其中e为自然对数的底数).
参考答案
7
2021普通高等学校招生全国统一考试·信息卷
数学(七)
一、1.D
【命题意图】本题考查一元二次不等式的解法,集合的补集、交集,体现了数学运算的核心素养.
【解析】∵A={0,1,2},,∴.故选D.
2.A
【命题意图】本题考查复数的除法运算、复数的几何意义,考查数形结合思想、转化与化归思想,体现了数学运算、直观想象等核心素养.
多法解题
方法一
.由复数的几何意义可知在复平面内,复数z2对应的点的轨迹是以原点为圆心的单位圆.如图,z1对应的向量为,z2对应的向量为,则.∴当B取单位圆与OA的交点时,有最小值,为.故选A.
方法二
z1=2-i.由复数的几何意义可知在复平面内,复数z1对应的向量,z2对应的向量,则
,其中,.当sin(θ-φ)=-1时,|z1-z2|取得最小值,为.故选A.
方法总结
关于两个复数之差的模的最值问题,可结合复数的几何意义,将其转化为向量的模的问题.求向量之差的模的最值,有两种方法:(1)几何法,将复数z2在复平面内对应的向量与单位圆联系起来,通过向量的运算求其最值;(2)代数法,利用,通过向量的数量积运算,构造关于θ的三角函数,利用其性质求最值.
3.B
【命题意图】本题考查不等式的性质,对数函数的单调性,充分条件、必要条件的判断,体现了数学运算、逻辑推理等核心素养.
【解析】.故“a>b”是“log0.5(2a-1)<log0.5(2b-1)”的必要不充分条件.故选B.
4.A
【命题意图】本题考查函数的单调性、奇偶性,利用函数的单调性解不等式,考查转化与化归思想,体现了数学运算、逻辑推理等核心素养.
【解析】由函数解析式可知,函数f(x)是定义在R上的奇函数,且单调递增,于是原不等式可化为f(2x-1)<-f(3)=f(-3),所以2x-1<-3,解得x<-1.故选A.
方法总结
用常规方法解答与函数的奇偶性、单调性有关的不等式问题,需要将不等式转化为f(g(x))≤f(h(x))的形式,再利用函数的单调性“脱去”最外层函数,转化为一般不等式.
名师评题
解本题时要撇开函数解析式的表象,抓住函数隐含的性质,如奇偶性和单调性(本题所给的函数既是奇函数又是增函数),然后利用性质巧妙解题,能很好地考查学生的数学功底和数学素养.本题如果解题方法选择不当,会耗时过多且容易出错.
5.B
【命题意图】本题考查函数图像的识别,体现了直观想象、逻辑推理等核心素养.
【解析】当x=0时,f(x)=0,排除A.
当0<x<π时,f(x)>0,排除D.
因为t>0,所以et>1.根据指数函数的性质,对于x0>0,.又因为|sin
x0|=|sin(-x0)|,所以|f(x0)|>|f(-x0)|,排除C.故选B.
6.B
【命题意图】本题考查抛物线的方程及其简单的几何性质、向量的数乘,体现了数学运算、直观想象等核心素养.
【解析】将点的坐标代入y2=2px(p>0),解得p=3,即抛物线C的方程为y2=6x.设准线l与x轴交于点A,则|AF|=3.过点Q作QQ1⊥l于点Q1,则|QQ1|=|FQ|.因为AF∥QQ1,,所以,所以,即.故选B.
7.C
【命题意图】本题考查三角函数的图像与性质,体现了逻辑推理、数学运算等核心素养.
【解析】由题意可知当时,取得最大值或最小值,所以
,k∈Z,所以,k∈Z.因为ω>0,所以当k=0时,ω取得最小值,此时f(x)的最小正周期.故选C.
8.B
【命题意图】本题考查平面向量的数量积、向量模的最大值、余弦定理的应用,考查数形结合思想、转化与化归思想,体现了数学运算、逻辑推理等核心素养.
【解析】由,得,∴PA⊥BC.又∵点P在线段BC上,∴△ABC为锐角三角形.设BC=x(x>3),则由余弦定理,得,解得x=4或x=2(舍去).如图,设BC的中点为H,连接AH,QH,则
,∴点Q在以AH为直径的圆上,如图,作出该圆.又∵AP⊥HP,∴点P也在以AH为直径的圆上,∴的最大值为该圆的直径,即AH.由余弦定理,得
,∴的最大值为.故选B.
二、9.ABC
【命题意图】本题考查回归方程、相关系数,体现了数学运算、数据分析等核心素养.
【解析】由r1>0或散点图(图略)可以得出y与x不呈负相关关系,A不正确.
是非线性回归方程,它的图像过样本中心点(6,172),B不正确.
注意表格中时间的单位是天而不是时(h),不能直接将x=10代入求解,C不正确.
这两个回归方程的相关系数均大于0.75,所以用这两个回归模型描述x和y之间的相关关系都有很好的效果,D正确.故选ABC.
10.ACD
【命题意图】本题考查函数的奇偶性、单调性、周期性,函数图像的对称性,体现了数学运算、逻辑推理等核心素养.
【解析】由题意得f(-x)=-f(x),g(-x)=-g(x).又g(x)=f(x-2),所以f(-x-2)=-f(x-2),即f(x+2)=f(x-2),所以函数f(x)是周期为4的周期函数,故A正确.因为f(x)的图像关于点(0,0)对称,周期为4,所以函数f(x)的图像关于点(4,0)对称,故C正确.由g(x)=f(x-2),得g(x+4)=f(x+2)=f(x+2-4)=f(x-2)=g(x),即函数g(x)是周期为4的周期函数,故B错误.由g(2)=f(2-2)=f(0),,g(5)=f(5-2)=f(3)=f(-1),且f(x)在(-2,2)上单调递增,得,所以,故D正确.选ACD.
11.AB
【命题意图】本题考查线线、线面、面面之间的位置关系,考查转化与化归思想,体现了逻辑推理、直观想象等核心素养.
【解析】如图,分别取棱AC,A1C1的中点D,E,连接DE,DM,ME,则DE∥CC1,DM∥BC.又DE∩DM=D,DE?平面MDE,DM?平面MDE,CC1?平面BCC1B1,BC?平面BCC1B1,所以平面MDE∥平面BCC1B1.要使MN∥平面BCC1B1,只需MN?平面MDE.又点N在侧面ACC1A1内(含边界),所以点N的轨迹就是线段DE,其长度等于侧棱长,故B正确.
易得直线MN与CC1是异面直线,故A正确.
因为不知道三棱柱ABC-A1B1C1是否为直三棱柱,且并不知其底面三角形ABC的具体形状,无法判断C,D是否正确.故选AB.
易错警示
棱柱上、下底面相互平行,侧面为平行四边形,故其侧面不一定垂直于底面.而直棱柱的侧面都垂直于底面,需注意区分.
12.ABD
【命题意图】本题考查与数列有关的新定义问题,考查转化与化归思想,体现了数学运算、逻辑推理等核心素养.
【解析】若{an}为等差数列,则an+2+an=2an+1,∴取A=2,B=-1即可,故A正确.
若{an}为等比数列,设公比为q,则由an+2=Aan+1+Ban,得anq2=Aq·an+Ban,则Aq+B=q2,∴对任意一个确定的等比数列{an},任取满足上述二元一次方程的A,B(AB≠0)均可,故B正确.
任取一周期大于2的周期数列(如1,2,3,1,2,3,…),易得A,B不存在,故C错误.
将A=B-1代入an+2=Aan+1+Ban,得an+2=(B-1)an+1+Ban,即an+2+an+1=B(an+1+an),∴.而,∴.∵A=B-1>0,∴B>1,∴,∴2S2n<T2n,故D正确.选ABD.
名师评题
本题设问新颖,具有一定的创新性.前3个选项熟悉而不俗套,以3个基本数列为背景,考查学生对概念、性质的深刻理解以及灵活运用的能力.第4个选项在计算S2n时要用到“并项法”,考查学生的灵活应变能力和创新能力,对计算方法和计算能力有着较高的要求,符合高考对运算能力的考查要求,不是进行繁难的运算,而是通过增加思维考核的深度,使学生去想怎么算,关键是“想”而不是“算”.
三、13.2
【命题意图】本题考查同角三角函数的基本关系、二倍角公式,体现了数学运算、逻辑推理等核心素养.
【解析】由,得,所以,于是
,解得tan
α=±2.又因为α是第三象限角,所以tan
α=2.
14.384
【命题意图】本题考查排列知识,体现了数学运算、逻辑推理等核心素养.
【解析】先排乙,有4个位置(不能排第一和第六的位置),再排甲,有4个位置(不能排乙所在的位置和第一的位置),剩下的四名同学随意排.故可能的情况数为.
技巧点拨
解本题的关键是注意“你们都没有获得冠军”这一条件,以及排甲、乙位置的顺序.
15.π
【命题意图】本题考查三棱锥及三棱锥的外接球的表面积,体现了数学运算、逻辑推理、直观想象等核心素养.
【解析】如图(1),设PP′与平面A′B′C′交于点H,则P′H为三棱锥P′-A′B′C′的高.由题意知PP′=1.设P′H=a(0<a<1),则△A′B′C′与△ABC的相似比为1-a,∴两者面积之比为(1-a)2.∴
,当且仅当2a=1-a,即时,取等号.易知,正四面体PABC的棱长为,∴当三棱锥P′-A′B′C′的体积最大时,正三角形A′B′C′的边长为.连接C′H,易知.设三棱锥P′-A′B′C′的外界球半径为r,球心为O,如图(2),取截面P′C′H分析.易知点O在直线P′H上,连接OC′,则,解得,∴三棱锥P′-A′B′C′的外接球的表面积S=4πr2=π.
方法总结
此类题目应分两步,首先确定三棱锥的体积何时最大,之后通过几何关系求出其外接球的半径.在求三棱锥体积函数V(a)的最值时,可利用基本不等式(需要巧妙地“凑”),也可求函数的导数,进而求出其体积最大时a的值.在求该三棱锥的外接球的半径时,需充分挖掘其几何关系,构造出直角三角形,利用勾股定理,建立关于r的方程.
知识拓展
在边长为a的正四面体PABC中,顶点P在底面正三角形ABC上的射影P′即为△ABC的重心(三边中线的交点),AP在底面上的射影AP′的长度为,正四面体的高PP′的长度为.掌握这些比例关系,可大大提高解题效率.
16.4
【命题意图】本题考查双曲线的定义、渐近线,圆的方程,直线与圆的位置关系,线段和的最值问题,考查转化与化归思想、数形结合思想,体现了数学运算、逻辑推理、直观想象等核心素养.
【解析】连接MF2,根据双曲线的定义,可知|MF1|=|MF2|+2a.圆E的标准方程为x2+(y-4)2=1,圆心E(0,4),半径为1,圆心E到直线,即的距离
,故该圆与双曲线的渐近线相离.于是|MF1|+|MN|=|MF2|+2a+|MN|≥|MF2|+2a+|ME|-1≥|EF2|+2a-1,所以当E,M,F2三点共线时,|MF1|+|MN|取到最小值,最小值为|EF2|+2a-1.由双曲线的渐近线方程为,不妨设a=2m(m>0),则,c=3m,所以
,所以,解得m=1,于是a=2,所以实轴长2a=4.
名师评题
高考对解析几何的考查十分注重对圆锥曲线的定义及性质的考查.本题考查了双曲线的定义、圆的性质以及平面几何中的最短距离问题,重点考查学生灵活运用定义和平面几何知识解决问题的能力.“解过无数问题,其实都是转化.”本题就是要把焦半径|MF1|转化到焦半径|MF2|,把点M到圆上动点的距离转化为到圆心(定点)的距离,很好地考查了学生的逻辑推理、直观想象、数学运算等核心素养.
四、17.【命题意图】本题考查等差数列、等比数列的性质,体现了逻辑推理、数学运算等核心素养.
【解】设等差数列{an}的公差为d,
则
整理,得解得
所以an=a1+(n-1)d=1+(n-1)×2=2n-1.
方案一:选条件①.
假设数列{bn}中存在某项bt使得b1,b3,bt成等比数列,则,即(λa3)2=λa1·λat.
因为λ≠0,所以.
又因为a3=2×3-1=5,a1=2×1-1=1,at=2t-1,
所以52=1·(2t-1),解得t=13.
所以存在正整数t=13使得b1,b3,bt成等比数列.
方案二:选条件②.
假设数列{bn}中存在某项bt使得b1,b3,bt成等比数列,则,即.
因为λ≠0,所以.
又因为a3=2×3-1=5,a1=2×1-1=1,at=2t-1,
所以52=1·(2t-1),解得t=13.
所以存在正整数t=13使得b1,b3,bt成等比数列.
方案三:选条件③.
假设数列{bn}中存在某项bt使得b1,b3,bt成等比数列,则,即(λ+a3)2=(λ+a1)·(λ+at),
若λ=2,则(2+a3)2=(2+a1)·(2+at),
将a3=2×3-1=5,a1=2×1-1=1,at=2t-1代入并整理,得3t=23,所以.
又t∈N
,所以不存在满足条件的正整数t.
18.【命题意图】本题考查正弦定理、余弦定理的应用,体现了数学运算、逻辑推理等核心素养.
【解】(1)∵,∴,即
,∴,∴.∵a<b,∴A<B,∴,∴.
(2)方法一
由正弦定理,得
,a=2Rsin
A=4sin
A.
设AB的中点为D,则在△BDC中,由余弦定理,得
CD2=BC2+BD2-2BC·BD·cos
B
.
由解得
.∴,∴,∴CD2∈(7,9),∴.∴AB边上的中线的取值范围为.
方法二
以△ABC的外接圆圆心O为坐标原点,建立如图的平面直角坐标系,使x轴与AB平行.
设AB的中点为D,连接OA,OB,OC,CD.
由正弦定理,得
,∴,∴,∴D(0,-1).
设C(2cos
θ,2sin
θ)(θ为射线OC与x轴非负半轴的夹角).
由题意,得
解得.∴.∵,∴7<5+4sin
θ<9,∴,∴AB边上的中线的取值范围为.
19.【命题意图】本题考查线面平行、利用空间向量求线面所成角的正弦值,考查转化与化归思想,体现了数学运算、逻辑推理、直观想象等核心素养.
(1)【证明】如图,连接BD,交AC于点O,连接OM,则O为BD的中点.
又∵M为PD的中点,∴OM为△PBD的中位线,∴OM∥PB.∵OM?平面ACM,PB?平面ACM,∴PB∥平面ACM.
(2)【解】取CP的中点N,连接ON.∵△PAB,△PAD均是以A为顶角的等腰直角三角形,∴PA⊥AB,PA⊥AD.
又∵AB∩AD=A,AB,AD?平面ABCD,∴PA⊥平面ABCD.∵O,N分别为AC,PC的中点,∴ON∥AP,∴ON⊥平面ABCD.
如图,以O为坐标原点,分别以直线OC,OB,ON为x轴、y轴、z轴建立空间直角坐标系O-xyz.
设AP=AB=2.∵∠ABC=60°,∴△ABC为等边三角形,∴OC=1,,,∴C(1,0,0),P(-1,0,2),.∴,,
.
设平面ACM的法向量为.
由得
令y=2,则.∴.
设PM与平面ACM所成的角为θ,与所成的角为α,则.∴PM与平面ACM所成角的正弦值为.
20.【命题意图】本题考查独立性检验、离散型随机变量的分布列及期望,体现了数学运算、数据分析等核心素养.
【解】(1)2×2列联表如下:
了解情况性别
了解
不了解
合计
男生
50
10
60
女生
25
15
40
合计
75
25
100
,∴没有99%的把握认为学生对服贸会的了解情况与性别有关.
(2)根据题意,抽取的5人中男生有3人,女生有2人.
从这5人中随机抽取3人,则男生人数ξ的所有可能取值为1,2,3,
则,
,
.∴ξ的分布列为
ξ
1
2
3
P
∴.
21.【命题意图】本题考查直线与椭圆的位置关系、轨迹方程的求解、向量数量积的坐标表示,体现了数学运算、直观想象、逻辑推理等核心素养.
【解】(1)由,得a=2,b=1.
设P(x1,y1),Q(x2,y2),则,且
①-②,得.
化简,得,∴,∴直线OM的方程为.
将代入椭圆C的方程,得.解得.∵点M的轨迹在椭圆C内,∴点M的轨迹方程为.
(2)设l:.
将代入椭圆方程并化简,得x2+2mx+2m2-2=0.
当Δ=4m2-4(2m2-2)=4(2-m2)>0时,
有
又∵,,∴
.∴为定值,且定值为-1.
方法总结
设而不求是指在解题过程中根据需要设出变量,但并不直接求出其具体值,而是利用某种关系(如和、差、积)来表示变量之间的关系.在解决圆锥曲线的有关问题时,能够达到“化难为易、化繁为简”的效果.
22.【命题意图】本题考查函数的极值问题、构造函数解答不等式的证明问题,考查转化与化归思想、方程思想,体现了数学运算、逻辑推理等核心素养.
(1)【解】由题意,得f(x)的定义域为(0,+∞).
.
由f(x)在其定义域内有两个极值点,可得方程f′(x)=0在x>0时有两个不相等的实数根,
即方程在x>0时有两个不相等的实数根.
设,则
.
令g′(x)=0,得,∴当时,g(x)单调递减;当时,g(x)单调递增.∴.
又∵当x→0时,g(x)→+∞;当x→+∞时,g(x)→0,∴.
综上可知,a的取值范围为.
(2)【证明】由题意,知∴
.∴要证,即证,即证x1x2>e.
不妨设,则即证.∵,g(x)在上单调递减,∴即证.
又∵g(x1)=g(x2)=a,∴即证,即证
,即证.
设,即证.
设
,
则,∴h(x)在[e2,+∞)上为增函数,∴.
综上可知,成立.
名师评题
导数题作为高考压轴题都有一定难度,对学生思维的深度有较高要求,学生除掌握必要的基础知识外,还需要有较强的观察力、想象力、应变力和逻辑推理能力.本题第(1)问比较常规,第(2)问除考查了分析法、消元法、换元法,方程思想、转化与划归思想,解法“简约而不简单”,需要步步为营、层层深入、随机应变,考查学生的数学素养,有着较高的区分度.
