19.2 第1课时 平面直角坐标系 课件(22张PPT)
文档属性
| 名称 | 19.2 第1课时 平面直角坐标系 课件(22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 700.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 16:35:24 | ||
图片预览




文档简介
导入新课
讲授新课
当堂练习
课堂小结
19.2 平面直角坐标系
第十九章 平面直角坐标系
第1课时 平面直角坐标系
学习目标
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标
等概念;(重点)
2.能在给定的直角坐标系中,由点的位置写出它的坐
标.(难点)
导入新课
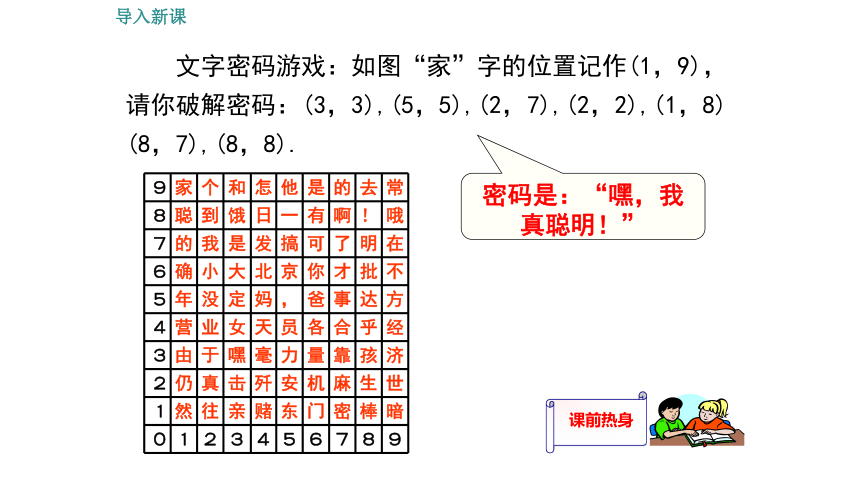
文字密码游戏:如图“家”字的位置记作(1,9),请你破解密码:(3,3),(5,5),(2,7),(2,2),(1,8)
(8,7),(8,8).
9
家
个
和
怎
他
是
的
去
常
8
聪
到
饿
日
一
有
啊
!
哦
7
的
我
是
发
搞
可
了
明
在
6
确
小
大
北
京
你
才
批
不
5
年
没
定
妈
,
爸
事
达
方
4
营
业
女
天
员
各
合
乎
经
3
由
于
嘿
毫
力
量
靠
孩
济
2
仍
真
击
歼
安
机
麻
生
世
1
然
往
亲
赌
东
门
密
棒
暗
0
1
2
3
4
5
6
7
8
9
密码是:“嘿,我真聪明!”
课前热身
导入新课
在平面内,确定物体位置方式主要有两种:
一般记作(a ,b)
(横 + 纵)
(方位角+距离)
在平面内,确定物体位置,需 _____ 数据
两个
思考:(a ,b)从何而来呢?
讲授新课
认识平面直角坐标系与平面内点的坐标
一
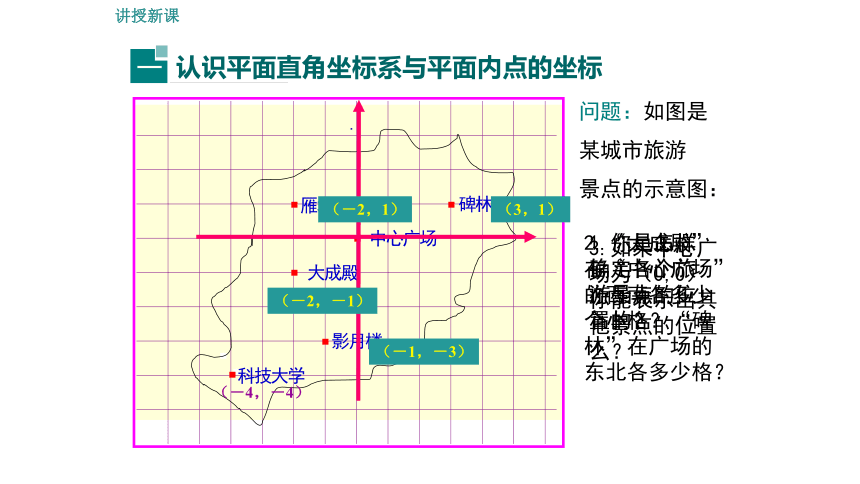
问题:如图是某城市旅游
景点的示意图:
(1) 你是怎样确定各个景点位置的?
(3,1)
(-2,1)
(-2,-1)
(-1,-3)
(-4,-4)
1.你是怎样确定各个旅游景点的位置的?
2.“大成殿”在“中心广场”的西南各多少个小格?“碑林”在广场的东北各多少格?
3.如果中心广场为(0,0)你能表示出其他景点的位置么?
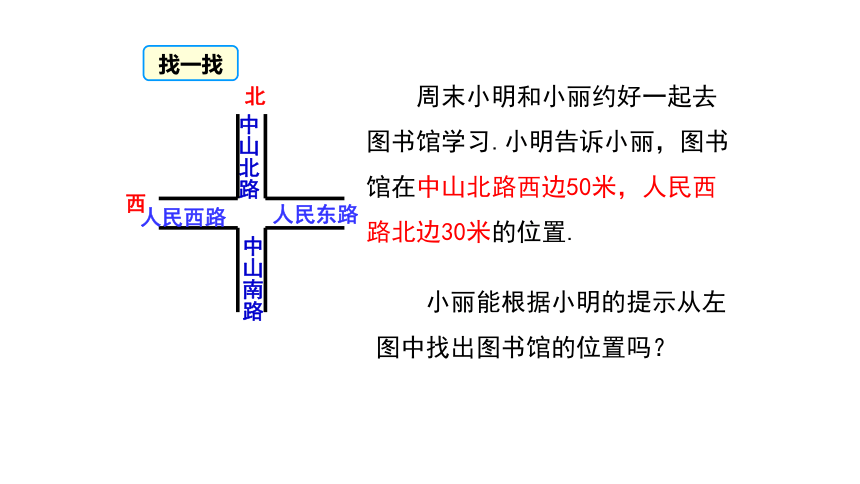
小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
中山南路
人民东路
中山北路
人民西路
北
西
找一找
中山南路
人民东路
中山北路
人民西路
北
西
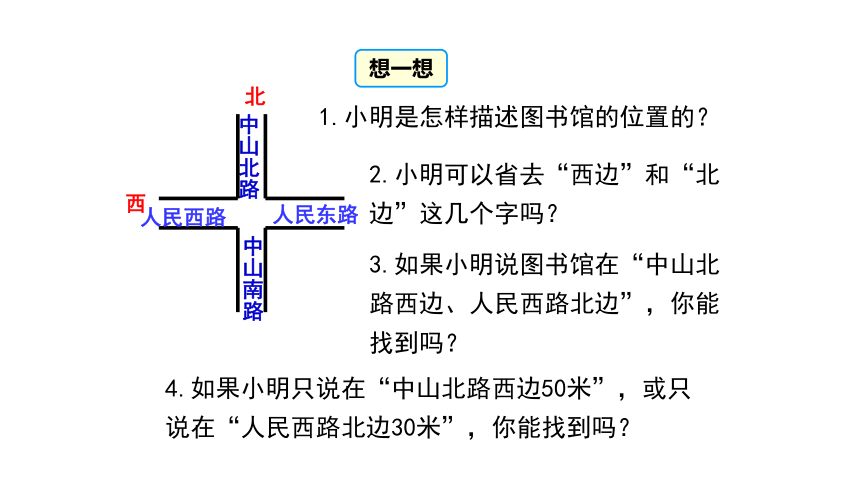
想一想
4.如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
1.小明是怎样描述图书馆的位置的?
2.小明可以省去“西边”和“北边”这几个字吗?
3.如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
若将中山路与人民路看着两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
3
1
4
2
5
-2
-4
-1
-3
O
y
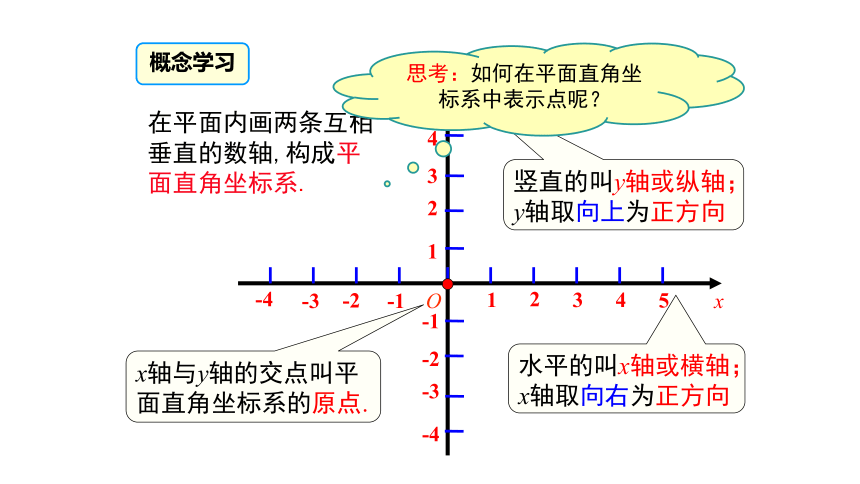
在平面内画两条互相垂直的数轴,构成平面直角坐标系.
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
概念学习
思考:如何在平面直角坐标系中表示点呢?
x
O
练一练:下面四个图形中,是平面直角坐标系的是( )
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3 2 1 -1 -2 -3
x
y
(B)
2
1
-1
-2
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上的坐标是3, 称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上的坐标是是-2,称为P点的横坐标.
P
N
M
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
O
A
(4,3)
x
y
1. 找出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
试一试
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
2. 在平面直角坐标系中
找点A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
典例精析
A
B
C
E
F
D
例:写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
在直角坐标系中描出下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
练一练
思考:坐标平面内的点与有序数对(坐标)是什么关系?
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
当堂练习
1.如图,点A的坐标为( )
A. ( -2,3)
B. ( 2,-3)
C . ( -2,-3)
D . ( 2,3)
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
A
2.如图,点A的坐标为 ,
点B的坐标为 .
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
B
(-2,0)
(0,-2)
3.某邮递员投递区域街道如图所示.现在,他要把一封邮件从邮政局所在地O处尽快送到A地.他选择的一条路径是
(0,0)→(0,3) →(4,3) →(4,8) →(7,8)
(1)用彩笔在图中标出邮递员走的这条路径.
(2)用坐标写出由点O到点A的其他最短的路径.
(1)图中黄线所示
(2)路径1:图中红线所示,坐标为(0,0) →(4,0) →(4,3) →(4,8) →(7,8);
路径2:图中蓝线所示,坐标为(0,0) →(4,0) →(7,0) →(7,8).
(2)用坐标写出由点O到点A的其他最短的路径.
A
B
C
D
E
4.下图是某植物园的平面示意图,A是大门,B、C、D、E分别表示梅、兰、菊、竹四个花圃.
请建立平面直角坐标系,写出各花圃的坐标.
hm
hm
解:以A点为原点,以水平方向为坐标轴建立直角坐标系,则
B(2,3),C(5,10),
D(8,8),E(11,9).
课堂小结
平面直角坐标系
平面直角坐标系的概念
在平面直角坐标系中描点
表示平面直角坐标系中点的坐标
讲授新课
当堂练习
课堂小结
19.2 平面直角坐标系
第十九章 平面直角坐标系
第1课时 平面直角坐标系
学习目标
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标
等概念;(重点)
2.能在给定的直角坐标系中,由点的位置写出它的坐
标.(难点)
导入新课
文字密码游戏:如图“家”字的位置记作(1,9),请你破解密码:(3,3),(5,5),(2,7),(2,2),(1,8)
(8,7),(8,8).
9
家
个
和
怎
他
是
的
去
常
8
聪
到
饿
日
一
有
啊
!
哦
7
的
我
是
发
搞
可
了
明
在
6
确
小
大
北
京
你
才
批
不
5
年
没
定
妈
,
爸
事
达
方
4
营
业
女
天
员
各
合
乎
经
3
由
于
嘿
毫
力
量
靠
孩
济
2
仍
真
击
歼
安
机
麻
生
世
1
然
往
亲
赌
东
门
密
棒
暗
0
1
2
3
4
5
6
7
8
9
密码是:“嘿,我真聪明!”
课前热身
导入新课
在平面内,确定物体位置方式主要有两种:
一般记作(a ,b)
(横 + 纵)
(方位角+距离)
在平面内,确定物体位置,需 _____ 数据
两个
思考:(a ,b)从何而来呢?
讲授新课
认识平面直角坐标系与平面内点的坐标
一
问题:如图是某城市旅游
景点的示意图:
(1) 你是怎样确定各个景点位置的?
(3,1)
(-2,1)
(-2,-1)
(-1,-3)
(-4,-4)
1.你是怎样确定各个旅游景点的位置的?
2.“大成殿”在“中心广场”的西南各多少个小格?“碑林”在广场的东北各多少格?
3.如果中心广场为(0,0)你能表示出其他景点的位置么?
小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
中山南路
人民东路
中山北路
人民西路
北
西
找一找
中山南路
人民东路
中山北路
人民西路
北
西
想一想
4.如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
1.小明是怎样描述图书馆的位置的?
2.小明可以省去“西边”和“北边”这几个字吗?
3.如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
若将中山路与人民路看着两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
3
1
4
2
5
-2
-4
-1
-3
O
y
在平面内画两条互相垂直的数轴,构成平面直角坐标系.
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
概念学习
思考:如何在平面直角坐标系中表示点呢?
x
O
练一练:下面四个图形中,是平面直角坐标系的是( )
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3 2 1 -1 -2 -3
x
y
(B)
2
1
-1
-2
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上的坐标是3, 称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上的坐标是是-2,称为P点的横坐标.
P
N
M
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
O
A
(4,3)
x
y
1. 找出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
试一试
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
2. 在平面直角坐标系中
找点A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
典例精析
A
B
C
E
F
D
例:写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
在直角坐标系中描出下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
练一练
思考:坐标平面内的点与有序数对(坐标)是什么关系?
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
当堂练习
1.如图,点A的坐标为( )
A. ( -2,3)
B. ( 2,-3)
C . ( -2,-3)
D . ( 2,3)
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
A
2.如图,点A的坐标为 ,
点B的坐标为 .
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
B
(-2,0)
(0,-2)
3.某邮递员投递区域街道如图所示.现在,他要把一封邮件从邮政局所在地O处尽快送到A地.他选择的一条路径是
(0,0)→(0,3) →(4,3) →(4,8) →(7,8)
(1)用彩笔在图中标出邮递员走的这条路径.
(2)用坐标写出由点O到点A的其他最短的路径.
(1)图中黄线所示
(2)路径1:图中红线所示,坐标为(0,0) →(4,0) →(4,3) →(4,8) →(7,8);
路径2:图中蓝线所示,坐标为(0,0) →(4,0) →(7,0) →(7,8).
(2)用坐标写出由点O到点A的其他最短的路径.
A
B
C
D
E
4.下图是某植物园的平面示意图,A是大门,B、C、D、E分别表示梅、兰、菊、竹四个花圃.
请建立平面直角坐标系,写出各花圃的坐标.
hm
hm
解:以A点为原点,以水平方向为坐标轴建立直角坐标系,则
B(2,3),C(5,10),
D(8,8),E(11,9).
课堂小结
平面直角坐标系
平面直角坐标系的概念
在平面直角坐标系中描点
表示平面直角坐标系中点的坐标
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
