湘教版七年级数学上册2.3代数式的值(共26张ppt)
文档属性
| 名称 | 湘教版七年级数学上册2.3代数式的值(共26张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 18:01:33 | ||
图片预览







文档简介
(共26张PPT)
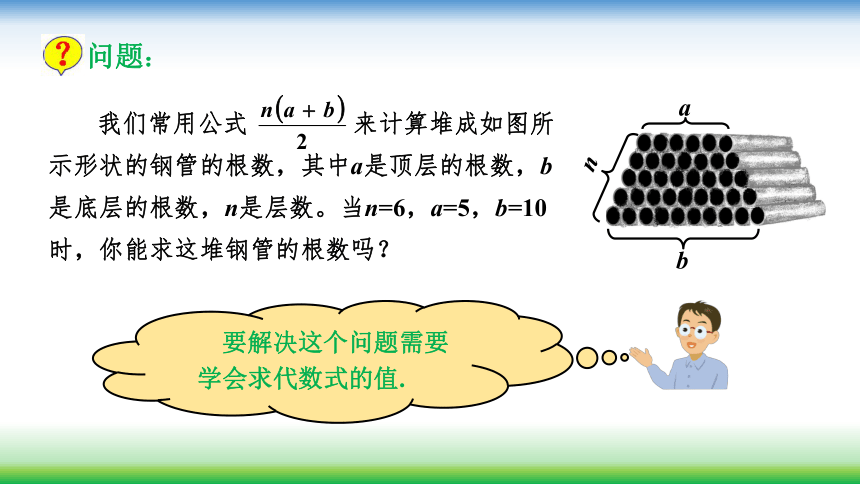
2.3
代
数
式
的
值
a=2
3a-1
3×2-1
5
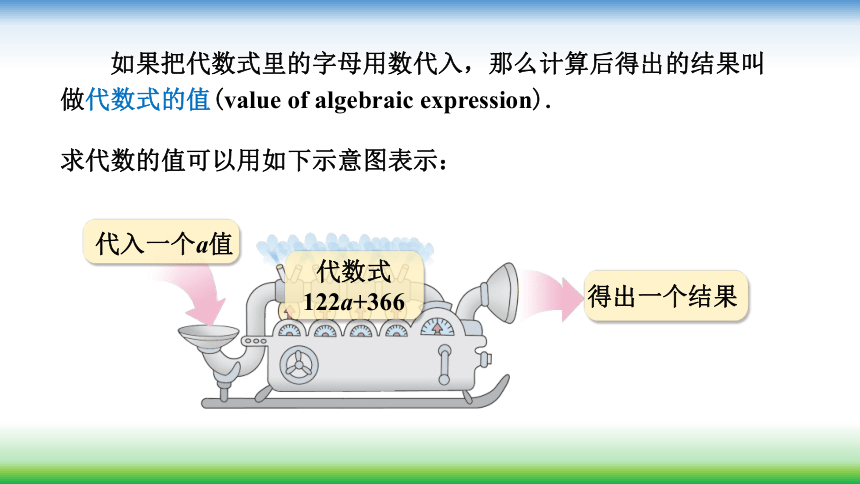
问题:
我们常用公式
来计算堆成如图所示形状的钢管的根数,其中a是顶层的根数,b是底层的根数,n是层数。当n=6,a=5,b=10时,你能求这堆钢管的根数吗?
n
a
b
要解决这个问题需要
学会求代数式的值.
学习目标
1.理解什么叫做代数式的值;
2.学会把代数式里的字母用数代入,把含字母的代数式转化为算式;
3.能正确地求出代数式的值;
4.体会特殊与一般的数学思维方法,提高数学应用能力;
5.通过解决生活中的数学问题,体验数学的价值,增强学习数学的动力.
动脑筋
今年植树节时,某校有305名同学参加了植
树活动,其中有
的同学每人植树a棵,其余同学每人植树2棵.
你能用代数式表示他们植树的总棵数吗?
如果a=3,他们共植树多少棵?
如果a=4,他们共植树多少棵?
=122a+366(棵).
他们共植树
他们植树的总棵数包括其中
的同学植树的棵数和其余同学植树的棵数,请你列出代数式并化简.
求当a=3时,他们共植树多少棵,可以把代数式122a+366中的字母a用数3代入,计算出结果。过程是:
a=3
122a+366
122×3+366
732(棵).
求当a=4时,他们共植树多少棵,可以把代数式122a+366中的字母a用数4代入,计算出结果。过程是:
a=4
122a+366
122×4+366
854(棵).
代入一个a值
代数式
122a+366
得出一个结果
如果把代数式里的字母用数代入,那么计算后得出的结果叫做代数式的值(value
of
algebraic
expression).
求代数的值可以用如下示意图表示:
代数式里的字母可以取各种不同的数值,但所取的数值必须使代数式和它表示的实际数量有意义,如上例
122a
+
366中的字母a不能取负数,又如
中的v不能取零.
解
(1)当x=-3时,
x2-3x+5
=(-3)2-3×(-3)+
5
=23
;
(2)当a=
0.5,
b=-2时,
(1)
当x=-3时,求
x2
-3x+5
的值;
(2)
当a=0.5,b=-2时,求
的值.
例1
我们在计算不规则图形的面积时,有时采用“方格
法”来计算.计算方法如下:假定每个小方格的边长为1个单位长,S为图形的面积,L是边界上的格数,N是内部格点数,则有
.
请根据此方法计算图中四边形ABCD的面积.
例2
解
由可知,边界上的格点数L=8,内部个点数N=12,所以四边形ABCD的面积为:
1.
填空:输入a的值
输出结果.
-2a+1
-4
4
0
-7
9
1
2.
当x=0.5,y=
0.79时,求代数式4x2+2y的值。
解
当x=0.5,y=
0.79时,
4x2+2y=4×0.5?+2×0.79=4×0.25+1.58=1+1.58=2.58.
3.
请用例2的方法求下图中图形的面积.
解
由可知,边界上的格点数L=14,内部格点数N=42,所以四边形ABCD的面积为:
4.请你查阅有关资料找出两个公式,再取适当的数值代入公式,求出结果.
提示:例如,初中数学中图形面积的计算公式;又如物理中电流的计算公式等.可查有关书籍,也可上网搜索.先写出公式,再取适当的数值代入公式,求出结果.
反思交流
1.什么叫做代数式的值?怎样求代数式的值?
2.你认为求代数式值要注意哪些细节?
3.怎样在实际问题中求代数式的值?
把代数式里的字母用数代入,计算后得出的结果叫做代数式的值.
把字母用数代入,注意在相同的位置把字母换成数,不改变原来的运算和运算顺序.
把代数式的字母用数代入,注意以下细节:
①恢复“×”号;
②负数加括号;
③分数的乘方把分数加括号.
解决实际问题要注意:
①根据数量关系列出正确的代数式,并化简;
②写出代数式中各字母的数值.
概括起来,求代数式的值需注意以下几点:
①写对代数式,明确字母的值;
②恢复“×”号;
③代入负数,分数(算乘方时)加括号;
④准确计算,运算和运算顺序不变.
1.填表:
a
-2
-1
0
0.5
3
4
3a-1
(3a-1)?
-7
-4
-2.5
-1
0.5
3.5
8
11
49
16
1
64
121
作业
习题2.3
=1-9+12-4
=
0.
2.当a=-1,b=-2,c=3时,求下列各式的值:
(1)
(2)
(3)
解
(1)
(2)
(3)
3.我们常用公式
来计算堆成如图所示形状的钢管的根数,其中a是顶层的根数,b是底层的根数,n是层数。当n=6,a=5,b=10时,你能求这堆钢管的根数吗?
解
当n=6,a=5,b=10时,
答:这堆钢管有45根.
4.根据一项科学研究,一个10岁至50岁的人每天所需的睡眠时间t(h)可用公式
计算出来,其中n代表这个人的岁数。根据这个公式,一个15岁的未成年人每天所需的睡眠时间是多少?
解:
=
9.5(h).
答:一个15岁的未成年人每天所需的睡眠时间是9.5h.
=3×1+2
=5.
5.
已知a?+2a=1,求3(a?+2a)+2的值.
解
把a?+2a=1代入3(a?+2a)+2,得
3(a?+2a)+2
把已知代数式看作一个整体,将它的值代入要求值的代数式,计算结果.
6.
如图,在一个边长为bcm的正方形的四角
各剪去一个半径为acm
的
圆。请用代数式表示红色部分的面积,并求当a=2,
b=6时红色部分的面积(结果保留π).
a
b
解
红色部分的面积是
,
当
a=2,b=6时,
答:红色部分的面积为(36-4π)cm.
同学们真是太棒了,加油!
2.3
代
数
式
的
值
a=2
3a-1
3×2-1
5
问题:
我们常用公式
来计算堆成如图所示形状的钢管的根数,其中a是顶层的根数,b是底层的根数,n是层数。当n=6,a=5,b=10时,你能求这堆钢管的根数吗?
n
a
b
要解决这个问题需要
学会求代数式的值.
学习目标
1.理解什么叫做代数式的值;
2.学会把代数式里的字母用数代入,把含字母的代数式转化为算式;
3.能正确地求出代数式的值;
4.体会特殊与一般的数学思维方法,提高数学应用能力;
5.通过解决生活中的数学问题,体验数学的价值,增强学习数学的动力.
动脑筋
今年植树节时,某校有305名同学参加了植
树活动,其中有
的同学每人植树a棵,其余同学每人植树2棵.
你能用代数式表示他们植树的总棵数吗?
如果a=3,他们共植树多少棵?
如果a=4,他们共植树多少棵?
=122a+366(棵).
他们共植树
他们植树的总棵数包括其中
的同学植树的棵数和其余同学植树的棵数,请你列出代数式并化简.
求当a=3时,他们共植树多少棵,可以把代数式122a+366中的字母a用数3代入,计算出结果。过程是:
a=3
122a+366
122×3+366
732(棵).
求当a=4时,他们共植树多少棵,可以把代数式122a+366中的字母a用数4代入,计算出结果。过程是:
a=4
122a+366
122×4+366
854(棵).
代入一个a值
代数式
122a+366
得出一个结果
如果把代数式里的字母用数代入,那么计算后得出的结果叫做代数式的值(value
of
algebraic
expression).
求代数的值可以用如下示意图表示:
代数式里的字母可以取各种不同的数值,但所取的数值必须使代数式和它表示的实际数量有意义,如上例
122a
+
366中的字母a不能取负数,又如
中的v不能取零.
解
(1)当x=-3时,
x2-3x+5
=(-3)2-3×(-3)+
5
=23
;
(2)当a=
0.5,
b=-2时,
(1)
当x=-3时,求
x2
-3x+5
的值;
(2)
当a=0.5,b=-2时,求
的值.
例1
我们在计算不规则图形的面积时,有时采用“方格
法”来计算.计算方法如下:假定每个小方格的边长为1个单位长,S为图形的面积,L是边界上的格数,N是内部格点数,则有
.
请根据此方法计算图中四边形ABCD的面积.
例2
解
由可知,边界上的格点数L=8,内部个点数N=12,所以四边形ABCD的面积为:
1.
填空:输入a的值
输出结果.
-2a+1
-4
4
0
-7
9
1
2.
当x=0.5,y=
0.79时,求代数式4x2+2y的值。
解
当x=0.5,y=
0.79时,
4x2+2y=4×0.5?+2×0.79=4×0.25+1.58=1+1.58=2.58.
3.
请用例2的方法求下图中图形的面积.
解
由可知,边界上的格点数L=14,内部格点数N=42,所以四边形ABCD的面积为:
4.请你查阅有关资料找出两个公式,再取适当的数值代入公式,求出结果.
提示:例如,初中数学中图形面积的计算公式;又如物理中电流的计算公式等.可查有关书籍,也可上网搜索.先写出公式,再取适当的数值代入公式,求出结果.
反思交流
1.什么叫做代数式的值?怎样求代数式的值?
2.你认为求代数式值要注意哪些细节?
3.怎样在实际问题中求代数式的值?
把代数式里的字母用数代入,计算后得出的结果叫做代数式的值.
把字母用数代入,注意在相同的位置把字母换成数,不改变原来的运算和运算顺序.
把代数式的字母用数代入,注意以下细节:
①恢复“×”号;
②负数加括号;
③分数的乘方把分数加括号.
解决实际问题要注意:
①根据数量关系列出正确的代数式,并化简;
②写出代数式中各字母的数值.
概括起来,求代数式的值需注意以下几点:
①写对代数式,明确字母的值;
②恢复“×”号;
③代入负数,分数(算乘方时)加括号;
④准确计算,运算和运算顺序不变.
1.填表:
a
-2
-1
0
0.5
3
4
3a-1
(3a-1)?
-7
-4
-2.5
-1
0.5
3.5
8
11
49
16
1
64
121
作业
习题2.3
=1-9+12-4
=
0.
2.当a=-1,b=-2,c=3时,求下列各式的值:
(1)
(2)
(3)
解
(1)
(2)
(3)
3.我们常用公式
来计算堆成如图所示形状的钢管的根数,其中a是顶层的根数,b是底层的根数,n是层数。当n=6,a=5,b=10时,你能求这堆钢管的根数吗?
解
当n=6,a=5,b=10时,
答:这堆钢管有45根.
4.根据一项科学研究,一个10岁至50岁的人每天所需的睡眠时间t(h)可用公式
计算出来,其中n代表这个人的岁数。根据这个公式,一个15岁的未成年人每天所需的睡眠时间是多少?
解:
=
9.5(h).
答:一个15岁的未成年人每天所需的睡眠时间是9.5h.
=3×1+2
=5.
5.
已知a?+2a=1,求3(a?+2a)+2的值.
解
把a?+2a=1代入3(a?+2a)+2,得
3(a?+2a)+2
把已知代数式看作一个整体,将它的值代入要求值的代数式,计算结果.
6.
如图,在一个边长为bcm的正方形的四角
各剪去一个半径为acm
的
圆。请用代数式表示红色部分的面积,并求当a=2,
b=6时红色部分的面积(结果保留π).
a
b
解
红色部分的面积是
,
当
a=2,b=6时,
答:红色部分的面积为(36-4π)cm.
同学们真是太棒了,加油!
同课章节目录
