湘教版七年级数学上册2.5整式的加法和减法第1课时(共23张ppt)
文档属性
| 名称 | 湘教版七年级数学上册2.5整式的加法和减法第1课时(共23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 57.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
找朋友,找朋友,
找到朋友手拉手。
不是朋友不聚首,
真心朋友一起走。
在多项式中,有些项也是朋友。
找到它们放一起,几项合并成一项。
__________
__________
2.5
整式的加减法
第1课时
合并同类项
复
习
我能答
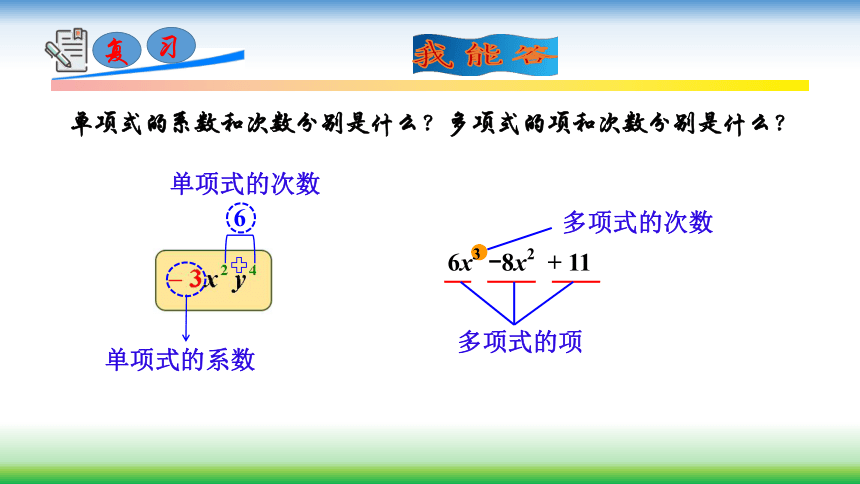
单项式的系数和次数分别是什么?多项式的项和次数分别是什么?
单项式的系数
6
单项式的次数
多项式的项
多项式的次数
6x3
-8x2
+
11
我
会
填
1.单项式4x?y的系数是
,次数是
;
2.单项式
的系数是
,次数是
;
3.多项式
是
次
项式,常数项是
;
4.多项式
中只有系数不同的项是
.
4
3
2
三
四
-1
ab和-2ab
7.运用乘法交换律计算:2a+3a=(
+
)a=5a.
6.用加法交换律和结合律计算:-4+11-7=
+11=-11+11=0;
5.用字母表示加法结合律:a+b+c=(
+
)+c=a+(
+
);
a
b
b
c
-4-7
2
3
学习目标
1.理解什么叫作同类项,并能正确找出多项式中的同类项;
2.掌握合并同类项的方法,能正确地合并同类项;
3.感知类比的数学思想,学会用类比的方法从旧知识抽象概括出新知识,
不断推动知识更新,提高学习数学的能力.
新
课
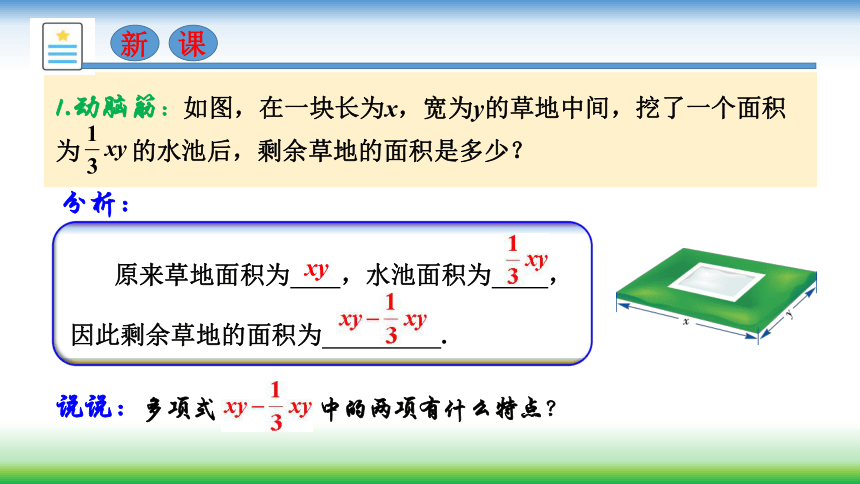
1.动脑筋:如图,在一块长为x,宽为y的草地中间,挖了一个面积为
的水池后,剩余草地的面积是多少?
原来草地面积为
,水池面积为
,
因此剩余草地的面积为
.
xy
分析:
说说:多项式
中的两项有什么特点?
像多项式
中的项xy、
,它们含有的字母相同,并且相同字母的指数也分别相同,称它们为同类项(like
term).
规定:
例如在多项式x2y+3x+1-4x-5x2y
-5中,同类项有x2y与-5x2y,3x与-4x,1与-5.
火
眼
金
睛
C
1.
下列每组中的两个单项式是同类项的是
(
)
A.
a与b
B.
-2xy?与3x?y
C.
4ab与ba
D.
与
.
同类项与字母的先后顺序无关.
2.下面多项式中与ab?是同类项的是
.
3.已知
是同类项,则x=
。
4ab?
1
因为字母表示数,所以可以利用交换律和结合律,先把3x和-4x调到一起,再逆向利用分配律,得
3x-4x=[3+(-4)]x=-x.
把x2y看作一个整体,那么利用上述方法可得,x2y-5x2y=[1+(-5)]x2y=-4x2y.
2.议一议:多项式
x2y+3x+1-4x-5x2y-5中的同类项可以合并吗?
利用交换律、结合律先将多项式中的同类项放在一起,再利用乘法分配律把同类项的系数相加,这样多项式中的同类项就合并了.
x2y+3x+1-4x-5x2y-5
=
x2y-5x2y+3x-4x+1-5
(交换律)
=
(1-5)x2y
+
(3-4)x
+(-4)(分配律)
=
(x2y
-
5x2y)+
(3x
-
4x)+(1
-
5)(结合律)
=
-4x2y-x-4
.
你能合并
吗?
合并同类项的过程如下:
把多项式的同类项合并成一项,叫作合并同类项(unite
like
terms).
例1
合并同类项:
(1)
(2)
解
(1)
(2)
注意:
x4的系数是1;
-x2y的系数是-1。
例2
合并同类项:
(1)
(2)
解
(1)
注意:
1.找出所有的同类项,不遗漏;
2.把同类项放到一起时,符号
必须随项搬。
(2)
标出同类项
将同类项放在一起
=
(1-2)xy3+(1+5)x3y+9
=
xy3-2xy3+x3y+5x3y+9
=
-xy3+6x3y+9.
把系数相加
合并同类项的方法:
像例2这样,先分别用不同的线标出不同的同类项,然后运用加法交换律和结合律,把同类项放在一起,最后把同类项的系数相加合并同类项.
熟练以后,可以不必把同类项调到一起而直接合并同类项.
小结:
议一议
多项式x?-4x?+7x?-2x-5与多项式x?+3x?-6x+4x-5相等吗?
两个式子合并同类项后都等于x?+3x?-2x-5.
两个多项式分别经过合并同类项后,如果它们的对应系数都相等,那么称这两个多项式相等.
1.请将下面的同类项用线连接起来:
2x3
xy2
-5x
-7xy2
3x
-4x3
作业
1.字母和字母的个数相同;
2.相同字母的指数相同.
同类项的特征:
3.常数项是同类项.
2.
合并同类项:
(1)
6x5-x5+9x5
;
(2)
-xy-4xy-7xy
;
(3)
8x4y
-6x4y
+15xy+9-2x4y;
(4)
5a?b+3ab?-11a?b-8ab?.
合并同类项三部曲:
①标出同类项(画线);
②把同类项放一起(分类放);
③合并同类项(把系数相加).
答案:(1)
14x5;
(2)
-12xy;
(3)
15xy+9;(3)
-6a?b-5ab?.
3.下列两个多项式是否相等?
x3-5x2+3x2-7x+2
,
x3-2x2+5x-12x+2
.
解:因为
x3-5x2+3x2-7x+2
=x3-2x2-7x+2,
x3-2x2+5x-12x+2
=x3-2x2-7x+2
.
化简后两个多项式对应项的系数相等,所以这两个多项式相等.
已知:A=3x?+2x-4+6x-2x?-8,B=ax?+bx-c,且A=B.
求:3a+2b-c的值。
题
思
考
反思总结
■
同类项的概念:
所含字母相同,并且相同字母的指数也相同的项.
一找二调,系数相加,字母及指数不变.
■
合并同类项的方法:
(系数可以不同,字母的顺序也可以不同.)
(熟练后:一找二并,直奔结果.)
找朋友,找朋友,
找到朋友手拉手。
不是朋友不聚首,
真心朋友一起走。
在多项式中,有些项也是朋友。
找到它们放一起,几项合并成一项。
__________
__________
2.5
整式的加减法
第1课时
合并同类项
复
习
我能答
单项式的系数和次数分别是什么?多项式的项和次数分别是什么?
单项式的系数
6
单项式的次数
多项式的项
多项式的次数
6x3
-8x2
+
11
我
会
填
1.单项式4x?y的系数是
,次数是
;
2.单项式
的系数是
,次数是
;
3.多项式
是
次
项式,常数项是
;
4.多项式
中只有系数不同的项是
.
4
3
2
三
四
-1
ab和-2ab
7.运用乘法交换律计算:2a+3a=(
+
)a=5a.
6.用加法交换律和结合律计算:-4+11-7=
+11=-11+11=0;
5.用字母表示加法结合律:a+b+c=(
+
)+c=a+(
+
);
a
b
b
c
-4-7
2
3
学习目标
1.理解什么叫作同类项,并能正确找出多项式中的同类项;
2.掌握合并同类项的方法,能正确地合并同类项;
3.感知类比的数学思想,学会用类比的方法从旧知识抽象概括出新知识,
不断推动知识更新,提高学习数学的能力.
新
课
1.动脑筋:如图,在一块长为x,宽为y的草地中间,挖了一个面积为
的水池后,剩余草地的面积是多少?
原来草地面积为
,水池面积为
,
因此剩余草地的面积为
.
xy
分析:
说说:多项式
中的两项有什么特点?
像多项式
中的项xy、
,它们含有的字母相同,并且相同字母的指数也分别相同,称它们为同类项(like
term).
规定:
例如在多项式x2y+3x+1-4x-5x2y
-5中,同类项有x2y与-5x2y,3x与-4x,1与-5.
火
眼
金
睛
C
1.
下列每组中的两个单项式是同类项的是
(
)
A.
a与b
B.
-2xy?与3x?y
C.
4ab与ba
D.
与
.
同类项与字母的先后顺序无关.
2.下面多项式中与ab?是同类项的是
.
3.已知
是同类项,则x=
。
4ab?
1
因为字母表示数,所以可以利用交换律和结合律,先把3x和-4x调到一起,再逆向利用分配律,得
3x-4x=[3+(-4)]x=-x.
把x2y看作一个整体,那么利用上述方法可得,x2y-5x2y=[1+(-5)]x2y=-4x2y.
2.议一议:多项式
x2y+3x+1-4x-5x2y-5中的同类项可以合并吗?
利用交换律、结合律先将多项式中的同类项放在一起,再利用乘法分配律把同类项的系数相加,这样多项式中的同类项就合并了.
x2y+3x+1-4x-5x2y-5
=
x2y-5x2y+3x-4x+1-5
(交换律)
=
(1-5)x2y
+
(3-4)x
+(-4)(分配律)
=
(x2y
-
5x2y)+
(3x
-
4x)+(1
-
5)(结合律)
=
-4x2y-x-4
.
你能合并
吗?
合并同类项的过程如下:
把多项式的同类项合并成一项,叫作合并同类项(unite
like
terms).
例1
合并同类项:
(1)
(2)
解
(1)
(2)
注意:
x4的系数是1;
-x2y的系数是-1。
例2
合并同类项:
(1)
(2)
解
(1)
注意:
1.找出所有的同类项,不遗漏;
2.把同类项放到一起时,符号
必须随项搬。
(2)
标出同类项
将同类项放在一起
=
(1-2)xy3+(1+5)x3y+9
=
xy3-2xy3+x3y+5x3y+9
=
-xy3+6x3y+9.
把系数相加
合并同类项的方法:
像例2这样,先分别用不同的线标出不同的同类项,然后运用加法交换律和结合律,把同类项放在一起,最后把同类项的系数相加合并同类项.
熟练以后,可以不必把同类项调到一起而直接合并同类项.
小结:
议一议
多项式x?-4x?+7x?-2x-5与多项式x?+3x?-6x+4x-5相等吗?
两个式子合并同类项后都等于x?+3x?-2x-5.
两个多项式分别经过合并同类项后,如果它们的对应系数都相等,那么称这两个多项式相等.
1.请将下面的同类项用线连接起来:
2x3
xy2
-5x
-7xy2
3x
-4x3
作业
1.字母和字母的个数相同;
2.相同字母的指数相同.
同类项的特征:
3.常数项是同类项.
2.
合并同类项:
(1)
6x5-x5+9x5
;
(2)
-xy-4xy-7xy
;
(3)
8x4y
-6x4y
+15xy+9-2x4y;
(4)
5a?b+3ab?-11a?b-8ab?.
合并同类项三部曲:
①标出同类项(画线);
②把同类项放一起(分类放);
③合并同类项(把系数相加).
答案:(1)
14x5;
(2)
-12xy;
(3)
15xy+9;(3)
-6a?b-5ab?.
3.下列两个多项式是否相等?
x3-5x2+3x2-7x+2
,
x3-2x2+5x-12x+2
.
解:因为
x3-5x2+3x2-7x+2
=x3-2x2-7x+2,
x3-2x2+5x-12x+2
=x3-2x2-7x+2
.
化简后两个多项式对应项的系数相等,所以这两个多项式相等.
已知:A=3x?+2x-4+6x-2x?-8,B=ax?+bx-c,且A=B.
求:3a+2b-c的值。
题
思
考
反思总结
■
同类项的概念:
所含字母相同,并且相同字母的指数也相同的项.
一找二调,系数相加,字母及指数不变.
■
合并同类项的方法:
(系数可以不同,字母的顺序也可以不同.)
(熟练后:一找二并,直奔结果.)
同课章节目录
