湘教版七年级数学上册2.5整式的加法和减法第3课时课件(15张)
文档属性
| 名称 | 湘教版七年级数学上册2.5整式的加法和减法第3课时课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
2.5
整式的加减(第3课时)
整式加减法的应用
名言警句
有了知识而不运用,如同一个农民耕地而不播种。——萨迪
1.能够熟练地求出多项式的和与差,能进行整式的化简并求值;
2.能够根据实际问题或几何图形的数量关系列出多项式解决一
些简单问题;
3.体会数形结合思想、整体思想在数学中的应用.
学
标
目
习
复
习
1.回答问题:
(1)
怎样合并同类项?
;
(2)
去括号的法则是什么?
;
(3)
如何进行整式的加减运算?
.
把系数相加,字母连同它的指数不变.
括号前是“+”,符号相同;括号前是“-”,符号相反.
先去括号,再合并同类项,结果按某个字母降(升)幂排列.
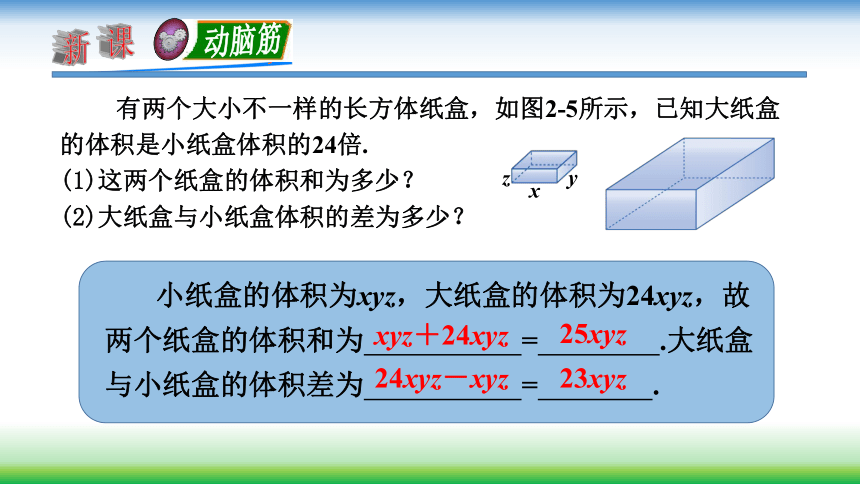
有两个大小不一样的长方体纸盒,如图2-5所示,已知大纸盒的体积是小纸盒体积的24倍.
(1)这两个纸盒的体积和为多少?
(2)大纸盒与小纸盒体积的差为多少?
x
y
z
新
课
动脑筋
小纸盒的体积为xyz,大纸盒的体积为24xyz,故两个纸盒的体积和为
=
.大纸盒
与小纸盒的体积差为
=
.
xyz+24xyz
25xyz
24xyz-xyz
23xyz
上面的例子告诉我们:在解决实际问题的时候,有时需要列出整式加减算式,求几个单项式或多项式的和或差。那么我们要怎样做呢?请看下面的例题。
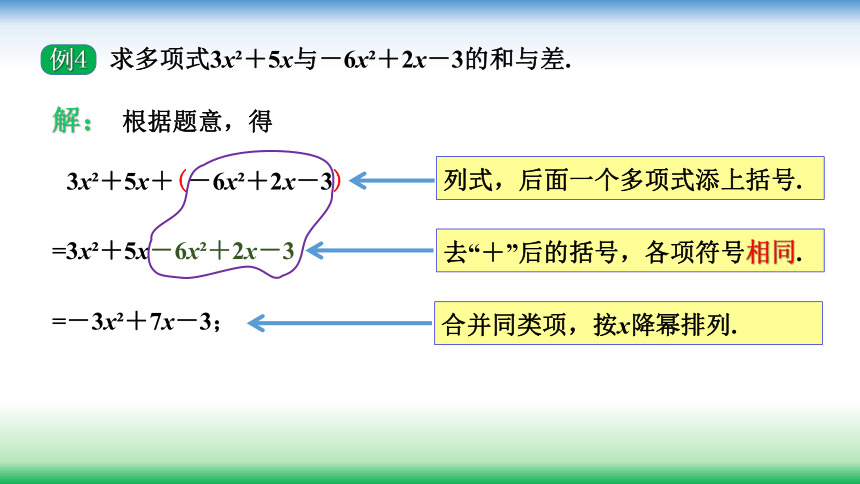
例4
求多项式3x?+5x与-6x?+2x-3的和与差.
3x?+5x+(-6x?+2x-3)
列式,后面一个多项式添上括号.
=3x?+5x-6x?+2x-3
去“+”后的括号,各项符号相同.
=-3x?+7x-3;
合并同类项,按x降幂排列.
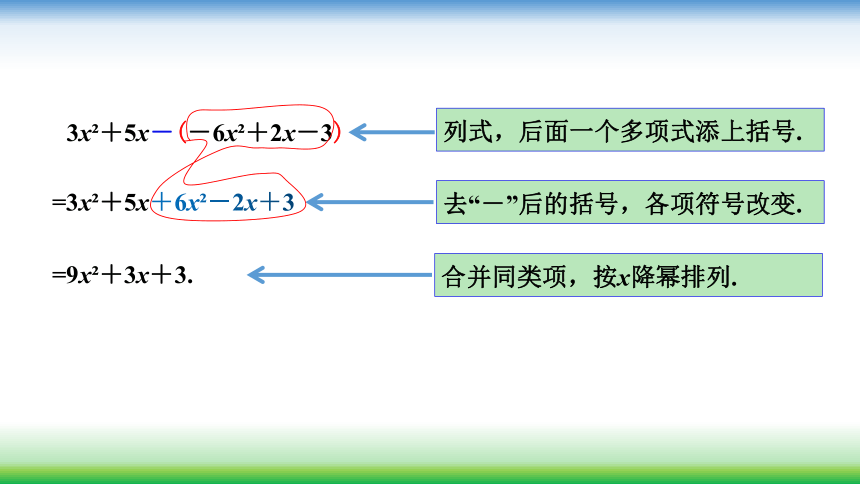
解:
根据题意,得
3x?+5x-(-6x?+2x-3)
列式,后面一个多项式添上括号.
=3x?+5x+6x?-2x+3
去“-”后的括号,各项符号改变.
=9x?+3x+3.
合并同类项,按x降幂排列.
例5
先化简,再求值:
5xy-(4x?+2xy)-2(2.5xy+10),其中x=1,y=-2.
解:
5xy-(4x?+2xy)-2(2.5xy+10)
=
5xy-4x?-2xy-5xy-20
=
-4x?-2xy-20.
当
x=1,y=-2时,
-4x?-2xy-20=-4×1?-2×1×(-2)-20=-20.
×
利用分配律:
把“-2”与括号内的每一项相乘.
一般地,求整式的值时,我们可以先将整式通过去括号、合并同类项将整式化简,再把字母的值代入化简后的多项式,计算比较简便。如果字母的值比较简单,如字母的值为0,1,-1等,也可以直接代入求值.
例6
如图,正方形的边长为x,用整式表示图中的阴影部分面积,并计算当x=4m时,阴影部分的面积(π取3.14).
x
x
解:
阴影部分的面积为
当x=4m时,
交流总结
1.列式计算多项式的和或差要注意些什么?
列式时要注意后面的多项式要添加括号;计算时,先去括号,再合并同类项.
特别注意括号前是“-”,去掉括号,每一项都要变号;还要注意不漏乘括号里面的项.
2.
怎样列出与图形有关的多项式?
根据每个图形的特点,以及图形的周长、面积、体积等计算公式分别列出多项式.
课堂练习
1.当
x=-3时,求7x2-3x2+(5x2-2)的值.
解
7x2-3x2+(5x2-2)
=7x2-3x2+5x2-2
=9x2-2.
当
x=-3时,
9x2×2=9×(-3)?
-2=9×9-2=79.
3.先化简,再求值.
3xy2-4x2-2(2xy2-3x2)-x2,其中x=0.5,
y=-0.5.
解:3xy2-4x2-2(2xy2-3x2)-x2
=3xy2-4x2-4xy2
+6x2-x2
=-xy2+x2.
当
x=0.5,
y=-0.5时,
-xy2+x2=-0.5×(-0.5)
?
+0.5?=-0.125+0.25=0.125.
题
思
考
美美在“计算多项式M加上2a?b-a?+4的和”时,不小心列成了减法算式,得出结果为4a?b。
请你写出多项式M,并帮美美计算出正确的结果。
2.5
整式的加减(第3课时)
整式加减法的应用
名言警句
有了知识而不运用,如同一个农民耕地而不播种。——萨迪
1.能够熟练地求出多项式的和与差,能进行整式的化简并求值;
2.能够根据实际问题或几何图形的数量关系列出多项式解决一
些简单问题;
3.体会数形结合思想、整体思想在数学中的应用.
学
标
目
习
复
习
1.回答问题:
(1)
怎样合并同类项?
;
(2)
去括号的法则是什么?
;
(3)
如何进行整式的加减运算?
.
把系数相加,字母连同它的指数不变.
括号前是“+”,符号相同;括号前是“-”,符号相反.
先去括号,再合并同类项,结果按某个字母降(升)幂排列.
有两个大小不一样的长方体纸盒,如图2-5所示,已知大纸盒的体积是小纸盒体积的24倍.
(1)这两个纸盒的体积和为多少?
(2)大纸盒与小纸盒体积的差为多少?
x
y
z
新
课
动脑筋
小纸盒的体积为xyz,大纸盒的体积为24xyz,故两个纸盒的体积和为
=
.大纸盒
与小纸盒的体积差为
=
.
xyz+24xyz
25xyz
24xyz-xyz
23xyz
上面的例子告诉我们:在解决实际问题的时候,有时需要列出整式加减算式,求几个单项式或多项式的和或差。那么我们要怎样做呢?请看下面的例题。
例4
求多项式3x?+5x与-6x?+2x-3的和与差.
3x?+5x+(-6x?+2x-3)
列式,后面一个多项式添上括号.
=3x?+5x-6x?+2x-3
去“+”后的括号,各项符号相同.
=-3x?+7x-3;
合并同类项,按x降幂排列.
解:
根据题意,得
3x?+5x-(-6x?+2x-3)
列式,后面一个多项式添上括号.
=3x?+5x+6x?-2x+3
去“-”后的括号,各项符号改变.
=9x?+3x+3.
合并同类项,按x降幂排列.
例5
先化简,再求值:
5xy-(4x?+2xy)-2(2.5xy+10),其中x=1,y=-2.
解:
5xy-(4x?+2xy)-2(2.5xy+10)
=
5xy-4x?-2xy-5xy-20
=
-4x?-2xy-20.
当
x=1,y=-2时,
-4x?-2xy-20=-4×1?-2×1×(-2)-20=-20.
×
利用分配律:
把“-2”与括号内的每一项相乘.
一般地,求整式的值时,我们可以先将整式通过去括号、合并同类项将整式化简,再把字母的值代入化简后的多项式,计算比较简便。如果字母的值比较简单,如字母的值为0,1,-1等,也可以直接代入求值.
例6
如图,正方形的边长为x,用整式表示图中的阴影部分面积,并计算当x=4m时,阴影部分的面积(π取3.14).
x
x
解:
阴影部分的面积为
当x=4m时,
交流总结
1.列式计算多项式的和或差要注意些什么?
列式时要注意后面的多项式要添加括号;计算时,先去括号,再合并同类项.
特别注意括号前是“-”,去掉括号,每一项都要变号;还要注意不漏乘括号里面的项.
2.
怎样列出与图形有关的多项式?
根据每个图形的特点,以及图形的周长、面积、体积等计算公式分别列出多项式.
课堂练习
1.当
x=-3时,求7x2-3x2+(5x2-2)的值.
解
7x2-3x2+(5x2-2)
=7x2-3x2+5x2-2
=9x2-2.
当
x=-3时,
9x2×2=9×(-3)?
-2=9×9-2=79.
3.先化简,再求值.
3xy2-4x2-2(2xy2-3x2)-x2,其中x=0.5,
y=-0.5.
解:3xy2-4x2-2(2xy2-3x2)-x2
=3xy2-4x2-4xy2
+6x2-x2
=-xy2+x2.
当
x=0.5,
y=-0.5时,
-xy2+x2=-0.5×(-0.5)
?
+0.5?=-0.125+0.25=0.125.
题
思
考
美美在“计算多项式M加上2a?b-a?+4的和”时,不小心列成了减法算式,得出结果为4a?b。
请你写出多项式M,并帮美美计算出正确的结果。
同课章节目录
