湘教版七年级上册数学第2章代数式复习知识要点及复习题解析(44张)
文档属性
| 名称 | 湘教版七年级上册数学第2章代数式复习知识要点及复习题解析(44张) |  | |
| 格式 | zip | ||
| 文件大小 | 20.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 20:36:42 | ||
图片预览










文档简介
(共44张PPT)
1.
理解代数式、整式、单项式、多项式等概念;
2.
进一步熟悉列代数式、求代数式的值的方法;
3.
掌握合并同类项、去括号法则,能正确地进行整
式的加、减法运算;
4.
能用整式解决实际中或图形中的有关问题;
5.
体会数学与生活的联系,感悟数学的博大精深。
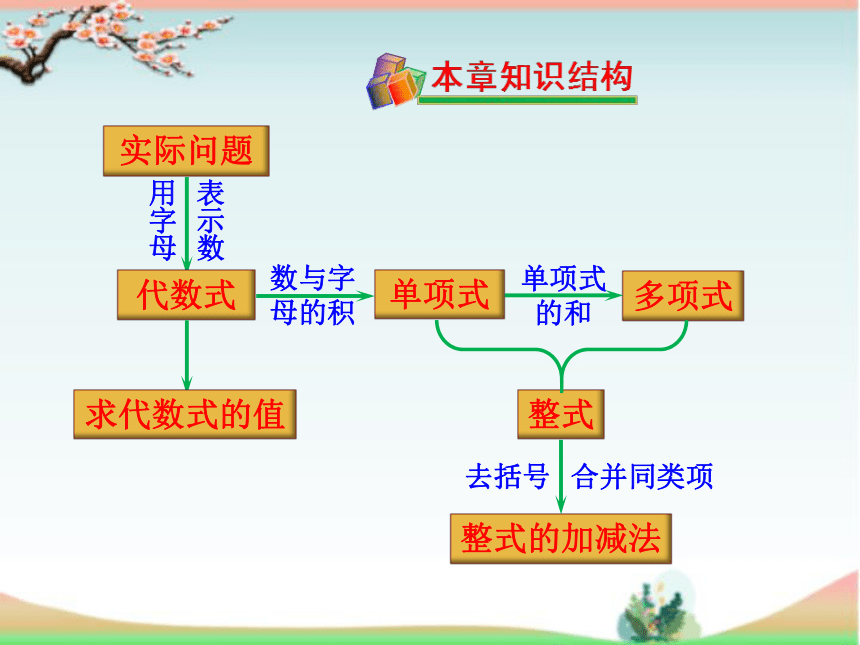
实际问题
用字母
代数式
整式
单项式
多项式
求代数式的值
数与字母的积
表示数
单项式的和
整式的加减法
去括号
合并同类项
把
用运算符号(加、减、乘、除、乘方等)连接起来的式子叫作代数式。
1.什么叫作代数式?什么叫作代数式的值?
把代数式里的字母用
代入,计算后所得的结果叫做代数式的值。
单独的
或者
也称代数式。
数和字母
一个数
一个字母
数
2.书写代数式要注意什么?
②数与字母相乘,数写在前面,省略乘号;
①字母与字母相乘,省略乘号;
③系数为带分数化成假分数;
④当系数是1或-1,1省略不写;
⑤整式相除,除号写成分数线;
⑥多项式后接单位,填上括号,如(2a+3b)元。
①实际问题:分析数量关系。
②图形:根据图形性质,运用相关公式。
①步骤:化简→代入→计算。
②注意:代入数时恢复乘号,代入的负数、有分
数的乘方添加括号,计算时不错数的符号。
3.如何列代数式?
4.怎样求代数式的值?
①
叫做单项式;
②单项式中的数字因数叫做这个单项的
;
③单项式中所有字母的指数的和叫做这个单项式
的
。
数与字母相乘的积
系数
次数
单独一个数或一个字母也是单项式。
6.什么叫作单项式?什么叫做单项式的系数和次数?
①
叫做多项式。
②组成多项式的单项式叫做多项式的
;
其中不含字母的项叫做
。
③多项式中
的次数和叫做多项式
的次数。
④单项式和多项式统称为
。
几个单项式的和
项
次数最高的项
整式
常数项
7.什么叫作多项式?什么叫做多项式的项和次数?
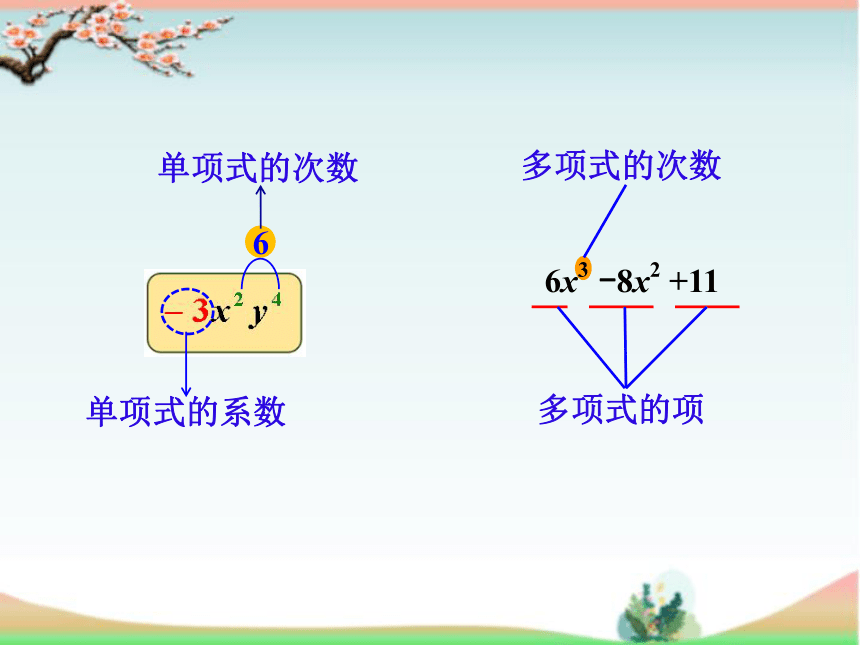
单项式的系数
6
多项式的项
多项式的次数
6x3
-8x2
+11
单项式的次数
①字母连同它的指数也相同的项叫做
。
②合并同类项:把
,字母连同指数
不变。
①括号前是“+”:去掉括号和“+”号,括号内各项
符号不变。
②括号前是“-”:去掉括号和“-”号,括号内各项
符号改变。
同类项
系数相加
8.什么叫作同类项?怎样合并同类项?
9.怎样去掉多项式中的括号?
10.怎样进行整式的加、减法运算?
①整式加减法的运算步骤:
先去括号,再合并同类项。
②降幂排列与升幂排列:
把多项式中的各项按某一个字母的次数从高到低排列叫做降幂排列,从低到高排列叫做升幂排列。
③两个多项式相等:
把多项式中去括号、合并同类项,并进行降幂或升幂排列,如果各项系数相等,则两多项式相等。
1.
括号前是“-”号,每项变号不漏项。
2.
括号外的数与括号内的项相乘,不漏乘。
下列运算错在哪里?请更正。
用代数式填空:
(1)某工厂的产量每年增长25%,如果第一年的产量是m,那么第二年、第三年的产量分别是
。
(2)已知x与y之间的关系如下表:
x
1
2
3
4
…
y
10
20+3
30+6
40+9
…
写出用x表示y的式子是
.
(1+25%)m,(1+25%)?m
y=10x+3(x-1)
【变式】观察下面一列单项式:
(1)直接写出第6个单项式:
.
(2)根据规律写出第n个单项式:
.
-6x64
n(-1)n+1x2n
D
4
2
若
,则
等于
(
)
B
【变式】已知
=0,则代数式
的值为
。
4
下列计算正确的是
(
)
【变式】已知a-c=4,b-c=6,则a-b等于
(
)
D
A
已知A=ab?-ab,A+B=2ab?-2.
⑴
直接写出B=
;
⑵
若ab=1,求A-B的值.
解:⑴
B=2ab?-2-(ab?-ab)
=2ab?-2-ab?+ab=ab?+ab-2.
⑵
A-B=ab?-ab-(ab?+ab-2)
=ab?-ab-ab?-ab+2
=-2ab+2.
当ab=1时,A-B=-2ab+2=-2×1+2=-2+2=2.
已知代数式:
(3a2–ab+2b2)–(a2–5ab+b2)–2(a2+2ab+b2)。
(1)试说明这个代数式的值与
a
的取值无关;
(2)若b=-2求这个代数式的值。
解:(1)(3a2–ab+2b2)–(a2–5ab+b2)–2(a2+2ab+b2)
=3a2–ab+2b2–a2+5ab–b2–2a2–4ab–2b2=–b2.
因为结果中不含的项,所以代数式的值与a的值无关。
(2)当b=-2
时,原式=-(-2)2
=-4
。
●A组基础题
1、用代数式填空:
(1)若圆的周长为2πrcm
,则圆的面积为
.
(2)某洗衣机厂原来库存洗衣机m台,现每天又生产n台存入库内,x
天后该厂库存洗衣机
台.
πr?cm?
(m+nx)
(3)如果b千克面粉售价n元,那么3kg面粉售价为
元.
(4)教室的后墙上贴满了长方形的壁纸。若后墙的面积为Sm?,每张壁纸长am
,宽bm,那么所贴壁纸的最少张数n=
(假定壁纸可以剪裁拼补).
(5)一辆汽车行驶akm后,又以vkm的速度行驶了th,那么这辆汽车所行驶的全部路程S=
km.
(a+vt)
2.列代数式:
(1)x的4倍与y的立方的差;
(2)x的相反数与y的倒数的和;
(3)a减去b的差的平方,再加上a与b的和的平方。
解:(1)4x-y?
(2)
(3)
3.写出下列代数式表示的实际意义:
(1)一个等边三角形的边长为a
,一个正方形的边长为
b,则3a+4b表示
;
这个等边三角形与这个正方形的周长的和
(2)若苹果每千克p元,橘子每千克q元,则代数式
50-(6p+4q)表示
.
用50元买6千克苹果和4千克橘子后剩下多少元
x
-3
-2
-1
0
1
2
3
y
18
7
0
-3
-2
3
12
4.设y=2x?﹣x﹣3,填写下表:
5.
当x=5,y=3时,求代数式
的值.
解:
6.某种濒危动物的数量每年以10%的速度减少,n年后该动物数量p与现有数量m之间的关系式是p=m(1-10%)n.如果该动物现有数量为8000只,那么3年后该动物还有多少只?
解:p=8000×(1-10%)3=5832(只)
7.说出下列单项式的系数和次数:
8.说出下列多项式的次数和常数项:
9.
写出3个多项式,要求每个多项式的次数不小于
3,项数不少于4项,其中至少有2项是同类项。
10.
计算:
(1)
(2)
(3)
解:(1)
(2)
(3)
(1)
3A-B;
(2)
A-3B.
解:(1)
3A-B
12、先化简,再求值:
(1)
(2)
(3)
其中
解:
(1)
当
x=-2时,原式=x=-2.
(2)
当
x=5,y=3时,原式=-4y=-4×3=-12.
本题结果与y值无关
(3)
当
时,
原式=
●B组提高题
13.先化简,再求值:
其中
当
时,
解:
14.燕尾槽的截面如图所示.
(1)用代数式表示图中红色部分的面积;
(2)若x=6,y=2,求红色部分的面积。
(1)y(x-y)
解:
(2)当x
=6
,y
=2时,
y(x-y)
=2×(6–2)=8.
15.从176.4m高处有一石头由静止开始自由下落,石头下落的高度h与时间t(0≤t≦6)有下面的关系:
时间t(s)
1
2
3
4
5
6
高度h(m)
4.9×1
4.9×4
4.9×9
4.9×16
4.9×25
4.9×36
(1)写出用时间t表示下落的高度h的公式;
(2)当t=3.5s时,求石头下落的高度。
解:
(1)
h=4.9t?
(0≤t≤6)
(2)
当
t=3.5时,h=4.9×3.5?=55.125(m).
●C组综合题
16.
如果-0.5mx
n?与5m4ny是同类项,求代数式的值:
题中代数式的项数较多,而且有括号,有同类项,直接求值比较复杂,先化简再求值比较简便。而根据同类项的定义,可以求出x、y的值。解答过程为:化简→求x、y的值→求代数式的值.
●C组综合题
解:
由-0.5mx
n?与5m4ny是同类项,得x=4,y=3.
原式=
所以,
17.
据有关资料统计,两个城市间每天的电话通话次数T与这两个城市的人口数a,b(单位:万人)及两城市间的距离d(单位:km)之间有下面关系式:
已知A
,B,C三个
城市的人口数及它们之
间的距离如图所示.如果A,B两个城市间每天的电话通话次数为t,求B
,C两个城市间每天的电话通话次数(用含t的代数式表示).
(k为常数)
先将A、B两个城市的人口数a=50,b=80,距离d=160及A、B两个城市每天的通话次数t,代入公式中,求出k。
再将B、C两个城市的人口数a=80,b=100,距离d=320及求得的用t表示k的式子,代入公式中,求出B、C两个城市每天的通话次数T.
解:由A、B两个城市之间每天的通话次数:
所以,B
、C两个城市间每天的电话通话次数为:
得
1.
理解代数式、整式、单项式、多项式等概念;
2.
进一步熟悉列代数式、求代数式的值的方法;
3.
掌握合并同类项、去括号法则,能正确地进行整
式的加、减法运算;
4.
能用整式解决实际中或图形中的有关问题;
5.
体会数学与生活的联系,感悟数学的博大精深。
实际问题
用字母
代数式
整式
单项式
多项式
求代数式的值
数与字母的积
表示数
单项式的和
整式的加减法
去括号
合并同类项
把
用运算符号(加、减、乘、除、乘方等)连接起来的式子叫作代数式。
1.什么叫作代数式?什么叫作代数式的值?
把代数式里的字母用
代入,计算后所得的结果叫做代数式的值。
单独的
或者
也称代数式。
数和字母
一个数
一个字母
数
2.书写代数式要注意什么?
②数与字母相乘,数写在前面,省略乘号;
①字母与字母相乘,省略乘号;
③系数为带分数化成假分数;
④当系数是1或-1,1省略不写;
⑤整式相除,除号写成分数线;
⑥多项式后接单位,填上括号,如(2a+3b)元。
①实际问题:分析数量关系。
②图形:根据图形性质,运用相关公式。
①步骤:化简→代入→计算。
②注意:代入数时恢复乘号,代入的负数、有分
数的乘方添加括号,计算时不错数的符号。
3.如何列代数式?
4.怎样求代数式的值?
①
叫做单项式;
②单项式中的数字因数叫做这个单项的
;
③单项式中所有字母的指数的和叫做这个单项式
的
。
数与字母相乘的积
系数
次数
单独一个数或一个字母也是单项式。
6.什么叫作单项式?什么叫做单项式的系数和次数?
①
叫做多项式。
②组成多项式的单项式叫做多项式的
;
其中不含字母的项叫做
。
③多项式中
的次数和叫做多项式
的次数。
④单项式和多项式统称为
。
几个单项式的和
项
次数最高的项
整式
常数项
7.什么叫作多项式?什么叫做多项式的项和次数?
单项式的系数
6
多项式的项
多项式的次数
6x3
-8x2
+11
单项式的次数
①字母连同它的指数也相同的项叫做
。
②合并同类项:把
,字母连同指数
不变。
①括号前是“+”:去掉括号和“+”号,括号内各项
符号不变。
②括号前是“-”:去掉括号和“-”号,括号内各项
符号改变。
同类项
系数相加
8.什么叫作同类项?怎样合并同类项?
9.怎样去掉多项式中的括号?
10.怎样进行整式的加、减法运算?
①整式加减法的运算步骤:
先去括号,再合并同类项。
②降幂排列与升幂排列:
把多项式中的各项按某一个字母的次数从高到低排列叫做降幂排列,从低到高排列叫做升幂排列。
③两个多项式相等:
把多项式中去括号、合并同类项,并进行降幂或升幂排列,如果各项系数相等,则两多项式相等。
1.
括号前是“-”号,每项变号不漏项。
2.
括号外的数与括号内的项相乘,不漏乘。
下列运算错在哪里?请更正。
用代数式填空:
(1)某工厂的产量每年增长25%,如果第一年的产量是m,那么第二年、第三年的产量分别是
。
(2)已知x与y之间的关系如下表:
x
1
2
3
4
…
y
10
20+3
30+6
40+9
…
写出用x表示y的式子是
.
(1+25%)m,(1+25%)?m
y=10x+3(x-1)
【变式】观察下面一列单项式:
(1)直接写出第6个单项式:
.
(2)根据规律写出第n个单项式:
.
-6x64
n(-1)n+1x2n
D
4
2
若
,则
等于
(
)
B
【变式】已知
=0,则代数式
的值为
。
4
下列计算正确的是
(
)
【变式】已知a-c=4,b-c=6,则a-b等于
(
)
D
A
已知A=ab?-ab,A+B=2ab?-2.
⑴
直接写出B=
;
⑵
若ab=1,求A-B的值.
解:⑴
B=2ab?-2-(ab?-ab)
=2ab?-2-ab?+ab=ab?+ab-2.
⑵
A-B=ab?-ab-(ab?+ab-2)
=ab?-ab-ab?-ab+2
=-2ab+2.
当ab=1时,A-B=-2ab+2=-2×1+2=-2+2=2.
已知代数式:
(3a2–ab+2b2)–(a2–5ab+b2)–2(a2+2ab+b2)。
(1)试说明这个代数式的值与
a
的取值无关;
(2)若b=-2求这个代数式的值。
解:(1)(3a2–ab+2b2)–(a2–5ab+b2)–2(a2+2ab+b2)
=3a2–ab+2b2–a2+5ab–b2–2a2–4ab–2b2=–b2.
因为结果中不含的项,所以代数式的值与a的值无关。
(2)当b=-2
时,原式=-(-2)2
=-4
。
●A组基础题
1、用代数式填空:
(1)若圆的周长为2πrcm
,则圆的面积为
.
(2)某洗衣机厂原来库存洗衣机m台,现每天又生产n台存入库内,x
天后该厂库存洗衣机
台.
πr?cm?
(m+nx)
(3)如果b千克面粉售价n元,那么3kg面粉售价为
元.
(4)教室的后墙上贴满了长方形的壁纸。若后墙的面积为Sm?,每张壁纸长am
,宽bm,那么所贴壁纸的最少张数n=
(假定壁纸可以剪裁拼补).
(5)一辆汽车行驶akm后,又以vkm的速度行驶了th,那么这辆汽车所行驶的全部路程S=
km.
(a+vt)
2.列代数式:
(1)x的4倍与y的立方的差;
(2)x的相反数与y的倒数的和;
(3)a减去b的差的平方,再加上a与b的和的平方。
解:(1)4x-y?
(2)
(3)
3.写出下列代数式表示的实际意义:
(1)一个等边三角形的边长为a
,一个正方形的边长为
b,则3a+4b表示
;
这个等边三角形与这个正方形的周长的和
(2)若苹果每千克p元,橘子每千克q元,则代数式
50-(6p+4q)表示
.
用50元买6千克苹果和4千克橘子后剩下多少元
x
-3
-2
-1
0
1
2
3
y
18
7
0
-3
-2
3
12
4.设y=2x?﹣x﹣3,填写下表:
5.
当x=5,y=3时,求代数式
的值.
解:
6.某种濒危动物的数量每年以10%的速度减少,n年后该动物数量p与现有数量m之间的关系式是p=m(1-10%)n.如果该动物现有数量为8000只,那么3年后该动物还有多少只?
解:p=8000×(1-10%)3=5832(只)
7.说出下列单项式的系数和次数:
8.说出下列多项式的次数和常数项:
9.
写出3个多项式,要求每个多项式的次数不小于
3,项数不少于4项,其中至少有2项是同类项。
10.
计算:
(1)
(2)
(3)
解:(1)
(2)
(3)
(1)
3A-B;
(2)
A-3B.
解:(1)
3A-B
12、先化简,再求值:
(1)
(2)
(3)
其中
解:
(1)
当
x=-2时,原式=x=-2.
(2)
当
x=5,y=3时,原式=-4y=-4×3=-12.
本题结果与y值无关
(3)
当
时,
原式=
●B组提高题
13.先化简,再求值:
其中
当
时,
解:
14.燕尾槽的截面如图所示.
(1)用代数式表示图中红色部分的面积;
(2)若x=6,y=2,求红色部分的面积。
(1)y(x-y)
解:
(2)当x
=6
,y
=2时,
y(x-y)
=2×(6–2)=8.
15.从176.4m高处有一石头由静止开始自由下落,石头下落的高度h与时间t(0≤t≦6)有下面的关系:
时间t(s)
1
2
3
4
5
6
高度h(m)
4.9×1
4.9×4
4.9×9
4.9×16
4.9×25
4.9×36
(1)写出用时间t表示下落的高度h的公式;
(2)当t=3.5s时,求石头下落的高度。
解:
(1)
h=4.9t?
(0≤t≤6)
(2)
当
t=3.5时,h=4.9×3.5?=55.125(m).
●C组综合题
16.
如果-0.5mx
n?与5m4ny是同类项,求代数式的值:
题中代数式的项数较多,而且有括号,有同类项,直接求值比较复杂,先化简再求值比较简便。而根据同类项的定义,可以求出x、y的值。解答过程为:化简→求x、y的值→求代数式的值.
●C组综合题
解:
由-0.5mx
n?与5m4ny是同类项,得x=4,y=3.
原式=
所以,
17.
据有关资料统计,两个城市间每天的电话通话次数T与这两个城市的人口数a,b(单位:万人)及两城市间的距离d(单位:km)之间有下面关系式:
已知A
,B,C三个
城市的人口数及它们之
间的距离如图所示.如果A,B两个城市间每天的电话通话次数为t,求B
,C两个城市间每天的电话通话次数(用含t的代数式表示).
(k为常数)
先将A、B两个城市的人口数a=50,b=80,距离d=160及A、B两个城市每天的通话次数t,代入公式中,求出k。
再将B、C两个城市的人口数a=80,b=100,距离d=320及求得的用t表示k的式子,代入公式中,求出B、C两个城市每天的通话次数T.
解:由A、B两个城市之间每天的通话次数:
所以,B
、C两个城市间每天的电话通话次数为:
得
同课章节目录
