北师大版九年级上册 第四章图形的相似复习(共18张ppt)
文档属性
| 名称 | 北师大版九年级上册 第四章图形的相似复习(共18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 343.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 18:37:51 | ||
图片预览






文档简介
第四章 图形的相似(复习)
复习目标:(1分钟)
1.巩固比例的有关性质,会用设k值的方法解题;
2.巩固黄金分割有关知识;
3.能熟练利用相似三角形的性质和判定解题.
1.若a、b、c、b成比例线段,则比例式为____________,或___________;
复习指导1:(2分钟)
结合所学知识点,完成下列填空:
a:b=c:d
ad=bc
_
或
(a,b,c,d都不为0)
那么____;
②若ad=bc,
则
_
①若 ,
3.比例的基本性质:
2.若a:b=b:c,或b?=ac,则b叫做a,c的________;
比例中项
检测1:(3分钟)
2.已知线段a=15 mm,b=3 cm,则线段a与b的比为 ;
4.若数a=1,b=4,则a、b的比例中项c= .
变式:若a=2m,d=8m,则a、d的比例中项b= .
3.已知a,b,c,d是成比例线段,其中a=4cm,b=2cm,c=8cm,则线段d的长为 cm
1.已知3x=4y(x≠0),则下列式子成立的是( )
B
1:2
4
±2
4m
b,c,a,d
16
---设k法
复习指导(二):(1分钟)
例
-5
检测(二):(3分钟)
1、已知
2、已知x:y:z=1:3:5,求
3.(2013?牡丹江)若2a=3b=4c,且abc≠0,
则 =___
14
-2
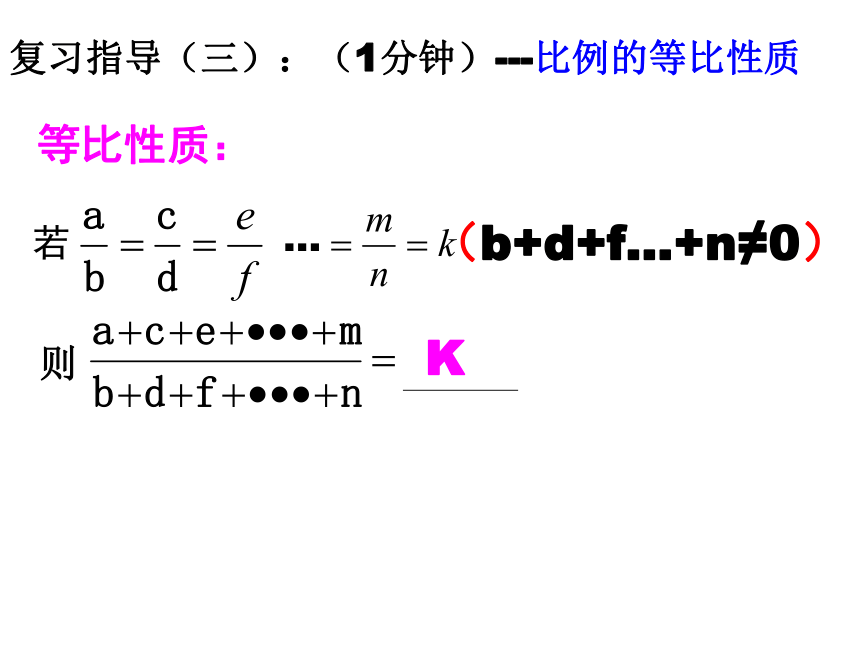
等比性质:
若
…
则
K
(b+d+f…+n≠0)
复习指导(三):(1分钟)---比例的等比性质
变:若
=k,则k=_______
2.如果
,那么
1.若
=6(b+d≠0),则
=______
6
2
-1
2或-1
检测(三):(3分钟)
复习指导(四):(2分钟)---黄金分割
1.如何判定点C是线段AB黄金分割点?
法1:
C
A
B
若 ,
则点C是线段AB黄金分割点
法2:
若 ,
则点C是线段AB黄金分割点
2.若点C是线段AB黄金分割点,
C
A
B
则AC= __ AB
BC= ___ AB
1.已知线段AB的长度为2,C是线段AB的黄金分割点,则AC= .
或
2.如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,AD>DE,BE交DC于点F,已知AB= ,则CF的长为 .
检测(四):(3分钟)
2
3.如图,△ABC中,AB=AC,∠BAC=108°,在BC边上取一点D,使BD=BA,连接AD.
求证:(1)△ADC∽△BAC;
(2)点D是BC的黄金分割点.
复习指导(五):(3分钟)---相似三角形的应用
例1小青同学想利用影长测量学校旗杆AB的高度.某一时刻他测得长1米的标杆的影长为1.4米,与此同时他发现旗杆AB的一部分影子BD落在地面上,另一部分影子CD落在楼房的墙壁上,分别测得其长度为11.2米和2米,如图所示.请你帮他求出旗杆AB的高度.
E
如图,某同学想测量旗杆的高度,他在某一时
刻测得1米长的竹竿竖直放置时影长1.5米,在
同时刻测量旗杆的影长时,因旗杆靠近一楼房,
影子不全落在地面上,有一部分落在墙上,他
测得落在地面上影长为21米,留在墙上的影高
为2米,求旗杆的高度.
变式:2分钟
E
例2如图,△ABC是一块锐角三角形材料,BC=120mm,高AD=80mm,要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
(1)设PN=x,PQ为y,求y关于x函数表达式
(2)当x为何值时,四边形PQMN为正方形.
(3分钟)
(3分钟) 变式: △ABC是一块锐角三角形材料,BC=120mm,高AD=80mm,要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
(1)设PN=x,矩形PQMN的面积为S,求S关于x的函数表达式,并指出x的取值范围.
(2)当x为何值时,矩形PQMN的面积最大?最大值是多少?
1.已知a,b, c是△ABC的三边长,周长为12,
且满足
(1)求a,b,c的值
(2)判断△ABC的形状
当堂训练(10分钟)
5,3,4
设 =k,
则a=3k-4,b=2k-3,c=4k-8
代入,求得k=3
k
则
K=3
2.Rt△ABC两条直角边AB=4cm,AC=3cm,点D沿AB从A向B运动,速度是1cm/秒,同时, 点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.
(1)当动点运动几秒时,△BDE与△ABC相似?
(2)设动点运动t秒时△ADE的面积为s,求s与t函数解析式;
(3)是否存在某一时刻t,使CD⊥DE?
F
复习目标:(1分钟)
1.巩固比例的有关性质,会用设k值的方法解题;
2.巩固黄金分割有关知识;
3.能熟练利用相似三角形的性质和判定解题.
1.若a、b、c、b成比例线段,则比例式为____________,或___________;
复习指导1:(2分钟)
结合所学知识点,完成下列填空:
a:b=c:d
ad=bc
_
或
(a,b,c,d都不为0)
那么____;
②若ad=bc,
则
_
①若 ,
3.比例的基本性质:
2.若a:b=b:c,或b?=ac,则b叫做a,c的________;
比例中项
检测1:(3分钟)
2.已知线段a=15 mm,b=3 cm,则线段a与b的比为 ;
4.若数a=1,b=4,则a、b的比例中项c= .
变式:若a=2m,d=8m,则a、d的比例中项b= .
3.已知a,b,c,d是成比例线段,其中a=4cm,b=2cm,c=8cm,则线段d的长为 cm
1.已知3x=4y(x≠0),则下列式子成立的是( )
B
1:2
4
±2
4m
b,c,a,d
16
---设k法
复习指导(二):(1分钟)
例
-5
检测(二):(3分钟)
1、已知
2、已知x:y:z=1:3:5,求
3.(2013?牡丹江)若2a=3b=4c,且abc≠0,
则 =___
14
-2
等比性质:
若
…
则
K
(b+d+f…+n≠0)
复习指导(三):(1分钟)---比例的等比性质
变:若
=k,则k=_______
2.如果
,那么
1.若
=6(b+d≠0),则
=______
6
2
-1
2或-1
检测(三):(3分钟)
复习指导(四):(2分钟)---黄金分割
1.如何判定点C是线段AB黄金分割点?
法1:
C
A
B
若 ,
则点C是线段AB黄金分割点
法2:
若 ,
则点C是线段AB黄金分割点
2.若点C是线段AB黄金分割点,
C
A
B
则AC= __ AB
BC= ___ AB
1.已知线段AB的长度为2,C是线段AB的黄金分割点,则AC= .
或
2.如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,AD>DE,BE交DC于点F,已知AB= ,则CF的长为 .
检测(四):(3分钟)
2
3.如图,△ABC中,AB=AC,∠BAC=108°,在BC边上取一点D,使BD=BA,连接AD.
求证:(1)△ADC∽△BAC;
(2)点D是BC的黄金分割点.
复习指导(五):(3分钟)---相似三角形的应用
例1小青同学想利用影长测量学校旗杆AB的高度.某一时刻他测得长1米的标杆的影长为1.4米,与此同时他发现旗杆AB的一部分影子BD落在地面上,另一部分影子CD落在楼房的墙壁上,分别测得其长度为11.2米和2米,如图所示.请你帮他求出旗杆AB的高度.
E
如图,某同学想测量旗杆的高度,他在某一时
刻测得1米长的竹竿竖直放置时影长1.5米,在
同时刻测量旗杆的影长时,因旗杆靠近一楼房,
影子不全落在地面上,有一部分落在墙上,他
测得落在地面上影长为21米,留在墙上的影高
为2米,求旗杆的高度.
变式:2分钟
E
例2如图,△ABC是一块锐角三角形材料,BC=120mm,高AD=80mm,要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
(1)设PN=x,PQ为y,求y关于x函数表达式
(2)当x为何值时,四边形PQMN为正方形.
(3分钟)
(3分钟) 变式: △ABC是一块锐角三角形材料,BC=120mm,高AD=80mm,要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
(1)设PN=x,矩形PQMN的面积为S,求S关于x的函数表达式,并指出x的取值范围.
(2)当x为何值时,矩形PQMN的面积最大?最大值是多少?
1.已知a,b, c是△ABC的三边长,周长为12,
且满足
(1)求a,b,c的值
(2)判断△ABC的形状
当堂训练(10分钟)
5,3,4
设 =k,
则a=3k-4,b=2k-3,c=4k-8
代入,求得k=3
k
则
K=3
2.Rt△ABC两条直角边AB=4cm,AC=3cm,点D沿AB从A向B运动,速度是1cm/秒,同时, 点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.
(1)当动点运动几秒时,△BDE与△ABC相似?
(2)设动点运动t秒时△ADE的面积为s,求s与t函数解析式;
(3)是否存在某一时刻t,使CD⊥DE?
F
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
