初中数学人教版八年级上册 14.1.1同底数幂的乘法课件(共20张ppt)
文档属性
| 名称 | 初中数学人教版八年级上册 14.1.1同底数幂的乘法课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1005.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 18:28:21 | ||
图片预览







文档简介
第十四章 整式的乘法与因式分解
14.1 整式的乘法
14.1.1同底数幂的乘法
人教版数学八年级上册
-----八年级29班全体师生欢迎各位老师的到来
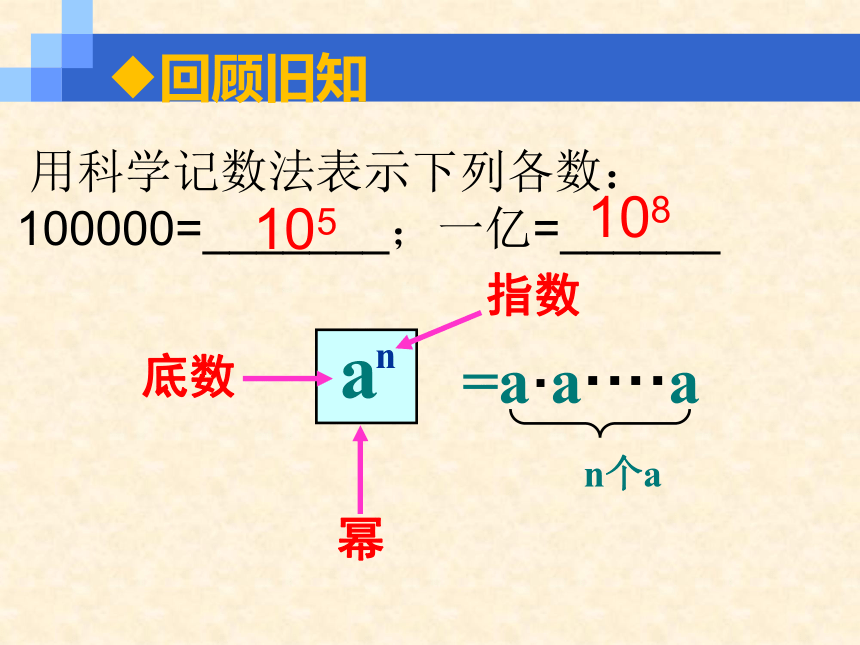
用科学记数法表示下列各数:100000=_______;一亿=______
回顾旧知
105
108
a
n
指数
幂
底数
=a·a····a
n个a
问题 观察算式107 ×105,两个因式有何特点?
观察可以发现,107 和105这两个因数底数相同,是同底数的幂的形式.
概念: 我们把形如107 ×105这种运算叫作同底数幂的乘法.
视频引入
自主学习课本第95页内容,然后完成探究。
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2× 2×2
=27
(2)a3·a2=a( )
=(a﹒a﹒a) (a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
自主学习
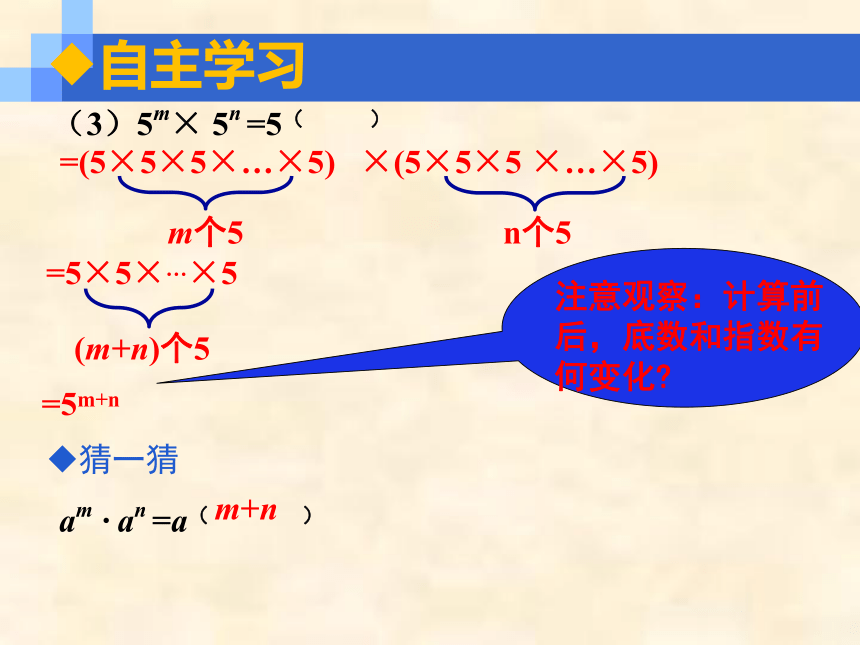
(3)5m× 5n =5( )
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
猜一猜
am · an =a( )
m+n
注意观察:计算前后,底数和指数有何变化?
自主学习
am·an
=(a·a·…a)
( 个a)
(a·a·…a)
( 个 a)
=(a·a·…a)
( __ 个a)
=a( )
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+ n
m+n
证一证
·
同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加
am · an = am+n (m、n都是正整数)
条件:①同底数的幂 ②乘法
结果:①底数不变 ②指数相加
要点归纳
自学检测
计算:
(1)x2·x5=__________________;
x2+5=x7
a1+6=a7
xm+3m+1
=x4m+1
(3)xm·x3m+1=__________________;
(2)a·a6=__________________;
a=a1
(1)a2· a6· a3 =(a2· a6) ·a3= ____
推广:am· an· ap =_____ (m,n,p都是正整数)
a11
(2)x· x2· x3 =(x· ____) ·___= ____
x2
x3
x6
am+n+p
(x+y)m·(x+y)n ______(x+y)m+n
=
合作探究
想一想
算一算
(-a)3=____
(x-y)3= - (y-x)3
(-2)8=256
a2
-a3
合作探究
算一算
(5)(x-y)2=(y-x)2
(4)(-a)2=__
(3)(-2)· (-2)4· (-2)3=____
(a+b)4·(a+b)7=(a+b)11
(x-y)2·(y-x)5= - (x-y)7
合作探究
例
想一想:am+n可以写成哪两个因式的积?
同底数幂乘法法则的逆用
am+n = am · an
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = · = × = ;
(2)x2m = · = × = ;
xm
xn
6
3
2
xm
xm
3
3
9
1.下列各式的结果等于26的是( )
A.2+25 B.2×25 C.23×25 D.0.22× 0.24
检测反馈
B
2.下列计算结果正确的是( )
A.a3·a3=a9 B.m2·n2=mn4
C.xm·x3=x3m D.y·yn=yn+1
检测反馈
D
3. 填空:x·x2·x( )=x7
4
4.计算:
(1) y4·y3·y2·y =_____.
(2)(a-b)2·(a-b)3=_____
(3) -a4·(-a)2=_____ ;
检测反馈
y10
(a-b)5
-a6
5.已知am=3,an=21,求am+n的值.
检测反馈
62
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
总结提升
作业布置
1.教材105页9、10.
2.配套练习一.
布置作业
谢谢大家!
14.1 整式的乘法
14.1.1同底数幂的乘法
人教版数学八年级上册
-----八年级29班全体师生欢迎各位老师的到来
用科学记数法表示下列各数:100000=_______;一亿=______
回顾旧知
105
108
a
n
指数
幂
底数
=a·a····a
n个a
问题 观察算式107 ×105,两个因式有何特点?
观察可以发现,107 和105这两个因数底数相同,是同底数的幂的形式.
概念: 我们把形如107 ×105这种运算叫作同底数幂的乘法.
视频引入
自主学习课本第95页内容,然后完成探究。
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2× 2×2
=27
(2)a3·a2=a( )
=(a﹒a﹒a) (a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
自主学习
(3)5m× 5n =5( )
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
猜一猜
am · an =a( )
m+n
注意观察:计算前后,底数和指数有何变化?
自主学习
am·an
=(a·a·…a)
( 个a)
(a·a·…a)
( 个 a)
=(a·a·…a)
( __ 个a)
=a( )
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+ n
m+n
证一证
·
同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加
am · an = am+n (m、n都是正整数)
条件:①同底数的幂 ②乘法
结果:①底数不变 ②指数相加
要点归纳
自学检测
计算:
(1)x2·x5=__________________;
x2+5=x7
a1+6=a7
xm+3m+1
=x4m+1
(3)xm·x3m+1=__________________;
(2)a·a6=__________________;
a=a1
(1)a2· a6· a3 =(a2· a6) ·a3= ____
推广:am· an· ap =_____ (m,n,p都是正整数)
a11
(2)x· x2· x3 =(x· ____) ·___= ____
x2
x3
x6
am+n+p
(x+y)m·(x+y)n ______(x+y)m+n
=
合作探究
想一想
算一算
(-a)3=____
(x-y)3= - (y-x)3
(-2)8=256
a2
-a3
合作探究
算一算
(5)(x-y)2=(y-x)2
(4)(-a)2=__
(3)(-2)· (-2)4· (-2)3=____
(a+b)4·(a+b)7=(a+b)11
(x-y)2·(y-x)5= - (x-y)7
合作探究
例
想一想:am+n可以写成哪两个因式的积?
同底数幂乘法法则的逆用
am+n = am · an
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = · = × = ;
(2)x2m = · = × = ;
xm
xn
6
3
2
xm
xm
3
3
9
1.下列各式的结果等于26的是( )
A.2+25 B.2×25 C.23×25 D.0.22× 0.24
检测反馈
B
2.下列计算结果正确的是( )
A.a3·a3=a9 B.m2·n2=mn4
C.xm·x3=x3m D.y·yn=yn+1
检测反馈
D
3. 填空:x·x2·x( )=x7
4
4.计算:
(1) y4·y3·y2·y =_____.
(2)(a-b)2·(a-b)3=_____
(3) -a4·(-a)2=_____ ;
检测反馈
y10
(a-b)5
-a6
5.已知am=3,an=21,求am+n的值.
检测反馈
62
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
总结提升
作业布置
1.教材105页9、10.
2.配套练习一.
布置作业
谢谢大家!
