沪教版(上海)初中数学八年级第一学期 19.2 证明举例 课件(22张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.2 证明举例 课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 964.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 20:40:56 | ||
图片预览





文档简介
1、判定两个三角形全等的方法有哪些?
复习
SAS ASA AAS SSS
2、如果已知两个三角形全等,我们能得到什么结论?
全等三角形的对应角、对应边相等
如图,在△ABC中,
(1)如果AB=AC,可得 ,
理由 .
(2)如果∠B=∠C,可得 ,
理由 .
复习
∠B=∠C
等边对等角
AB=AC
等角对等边
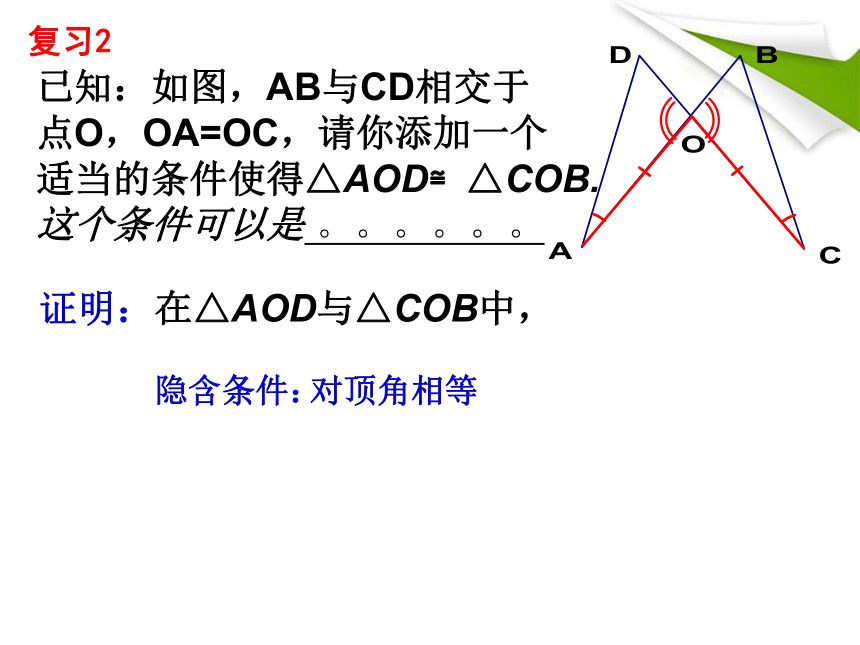
已知:如图,AB与CD相交于
点O,OA=OC,请你添加一个
适当的条件使得△AOD≌△COB.
这个条件可以是 。。。。。。
证明:在△AOD与△COB中,
复习2
隐含条件:
对顶角相等
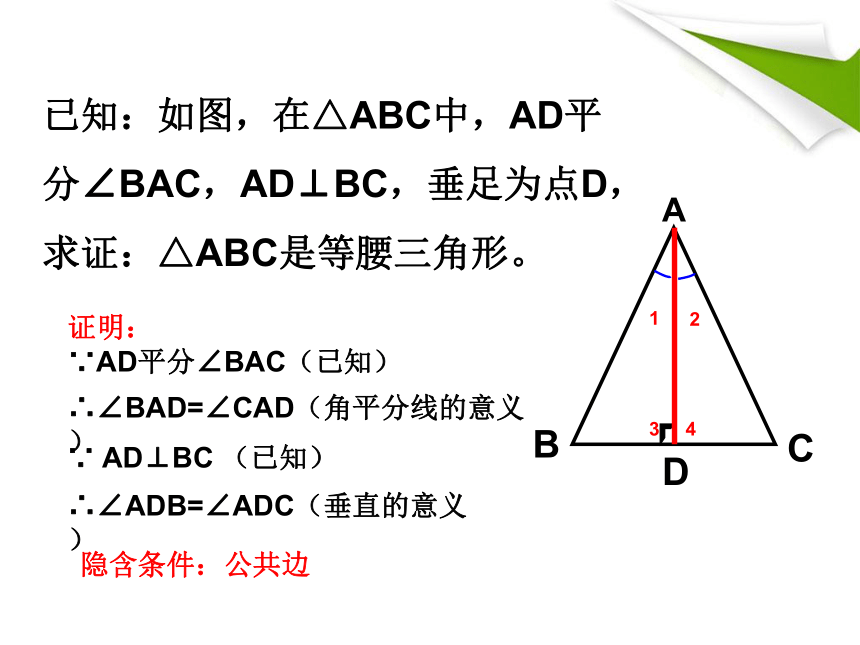
已知:如图,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,
求证:△ABC是等腰三角形。
A
B
C
D
证明:
∵AD平分∠BAC(已知)
∴∠BAD=∠CAD(角平分线的意义)
∴∠ADB=∠ADC(垂直的意义)
∵ AD⊥BC (已知)
隐含条件:公共边
1
2
3
4
例题1 已知:如图,AC与BD相交于点O,
OA=OD,∠OBC=∠OCB.
由条件你可以得到哪些结论?
求证:AB=DC.
A
C
B
D
O
1
2
C
A
B
D
O
1
2
练习1 已知:如图,AB=AC,∠B=∠C.
求证: DB=DC.
A
C
B
D
?
?
1
3
2
4
C
B
D
A
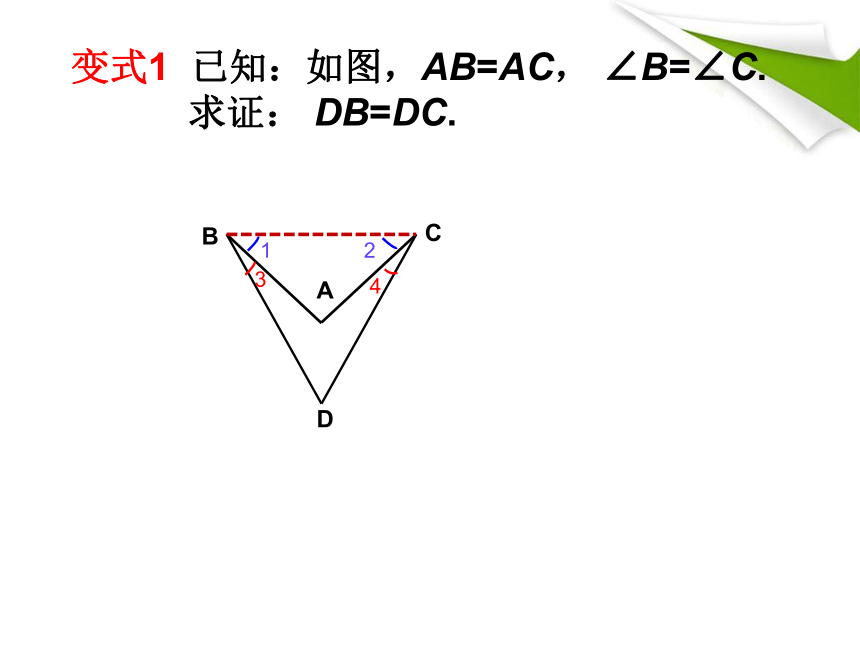
变式1 已知:如图,AB=AC, ∠B=∠C.
求证: DB=DC.
1
2
3
4
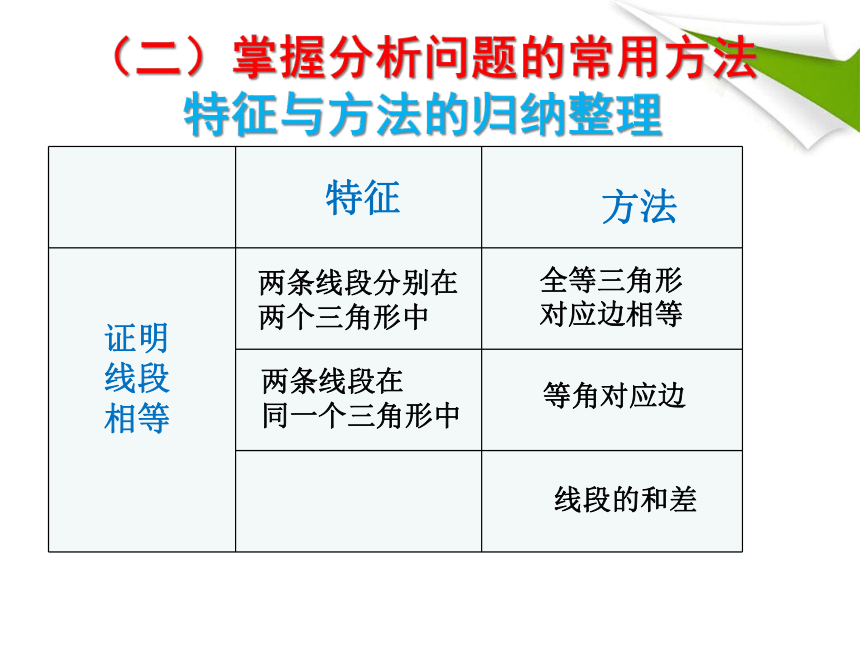
(二)掌握分析问题的常用方法
特征与方法的归纳整理
证明
线段
相等
特征
方法
两条线段分别在
两个三角形中
两条线段在
同一个三角形中
全等三角形
对应边相等
等角对应边
线段的和差
A
C
B
D
例题2 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.
例题2 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.
A
C
B
D
1
2
3
4
(三)掌握分析问题的常用方法
特征与方法的归纳整理
证明
角
相等
特征
方法
两条线段分别在
两个三角形中
两条线段在
同一个三角形中
全等三角形
对应边相等
等角对应边
角的和差
练习2 已知:如图,AB=AC, AD=AE,AB、DC相交于点M,AC、
BE相交于点N,∠DAB=∠EAC.
求证: ∠D = ∠E .
1
2
练习2 已知:如图,PB=PC,CE、BD相交于点P,∠BDA=∠CEA.
求证:AB=AC.
C
E
A
B
D
P
1
2
今天你学会了哪些知识?
(1)要证明两条线段相等、两个角相等,一般可以与两个全等三角形或者一个等腰三角形联系起来(也可以通过线段和差或角的和差来实现).
(2)有时全等三角形或等腰三角形并不存在,则需添置辅助线构造出相应的三角形.
小 结:
作业:
练习册19.2(2)
证明线段、角相等
线段、角分别在两个三角形中
证明(构造)全等三角形
线段、角在同一个三角形中
证明(构造)等腰三角形
与其它线段、角有无关联
利用中间线段、角代换
继续探究、尝试其它方法
是
是
是
否
否
否
小
结:
小 结:
今天你学会了哪些知识?
C
B
D
A
变式1 已知:如图,AB=AC, DB=DC.
求证: ∠B=∠C.
课外拓展1:小明特别喜欢做几何证明题,有一天他在研究等腰三角形时,有一个十分有趣的发现:
如图,在△ABC中,AB=AC,若在腰AB上取一点D,在腰AC的延长线上也取一点F,连结DF交BC于点E,只要满足BD=CF,则DE和EF之间始终有一个固定关系,你能猜出是什么关系吗?
D
C
B
A
E
F
欧几里德-人物简介
?欧几里得 Euclid? 约公元前 325年
—公元前 265年, 古希腊数学家,以
其所著的《几何原本》(简称《原本》)闻名于曾受业于柏拉图学园。后应埃及托勒密国王邀请,在雅典移居亚历山大,从事数学教学和研究工作。他一生治学严谨。所著《几何原本》13卷,是世界上最早公理化的教学著作,影响着历代科学文化的发展和科技人才培养。牛顿数学、物理学的研究,爱因斯坦相对论的创立,都是他们精通并善于应用几何学是分不开的。
课外拓展2:
已知:如图,AB=AC,BD=CD.
求证:△ABD≌△ACD.
证明:在△ABD与△ACD中,
∴ △ABD≌△ACD( ).
AB=AC
BD=CD
AD=AD
已知
已知
公共边
SSS
复习3
隐含条件:
公共边相等
复习
SAS ASA AAS SSS
2、如果已知两个三角形全等,我们能得到什么结论?
全等三角形的对应角、对应边相等
如图,在△ABC中,
(1)如果AB=AC,可得 ,
理由 .
(2)如果∠B=∠C,可得 ,
理由 .
复习
∠B=∠C
等边对等角
AB=AC
等角对等边
已知:如图,AB与CD相交于
点O,OA=OC,请你添加一个
适当的条件使得△AOD≌△COB.
这个条件可以是 。。。。。。
证明:在△AOD与△COB中,
复习2
隐含条件:
对顶角相等
已知:如图,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,
求证:△ABC是等腰三角形。
A
B
C
D
证明:
∵AD平分∠BAC(已知)
∴∠BAD=∠CAD(角平分线的意义)
∴∠ADB=∠ADC(垂直的意义)
∵ AD⊥BC (已知)
隐含条件:公共边
1
2
3
4
例题1 已知:如图,AC与BD相交于点O,
OA=OD,∠OBC=∠OCB.
由条件你可以得到哪些结论?
求证:AB=DC.
A
C
B
D
O
1
2
C
A
B
D
O
1
2
练习1 已知:如图,AB=AC,∠B=∠C.
求证: DB=DC.
A
C
B
D
?
?
1
3
2
4
C
B
D
A
变式1 已知:如图,AB=AC, ∠B=∠C.
求证: DB=DC.
1
2
3
4
(二)掌握分析问题的常用方法
特征与方法的归纳整理
证明
线段
相等
特征
方法
两条线段分别在
两个三角形中
两条线段在
同一个三角形中
全等三角形
对应边相等
等角对应边
线段的和差
A
C
B
D
例题2 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.
例题2 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.
A
C
B
D
1
2
3
4
(三)掌握分析问题的常用方法
特征与方法的归纳整理
证明
角
相等
特征
方法
两条线段分别在
两个三角形中
两条线段在
同一个三角形中
全等三角形
对应边相等
等角对应边
角的和差
练习2 已知:如图,AB=AC, AD=AE,AB、DC相交于点M,AC、
BE相交于点N,∠DAB=∠EAC.
求证: ∠D = ∠E .
1
2
练习2 已知:如图,PB=PC,CE、BD相交于点P,∠BDA=∠CEA.
求证:AB=AC.
C
E
A
B
D
P
1
2
今天你学会了哪些知识?
(1)要证明两条线段相等、两个角相等,一般可以与两个全等三角形或者一个等腰三角形联系起来(也可以通过线段和差或角的和差来实现).
(2)有时全等三角形或等腰三角形并不存在,则需添置辅助线构造出相应的三角形.
小 结:
作业:
练习册19.2(2)
证明线段、角相等
线段、角分别在两个三角形中
证明(构造)全等三角形
线段、角在同一个三角形中
证明(构造)等腰三角形
与其它线段、角有无关联
利用中间线段、角代换
继续探究、尝试其它方法
是
是
是
否
否
否
小
结:
小 结:
今天你学会了哪些知识?
C
B
D
A
变式1 已知:如图,AB=AC, DB=DC.
求证: ∠B=∠C.
课外拓展1:小明特别喜欢做几何证明题,有一天他在研究等腰三角形时,有一个十分有趣的发现:
如图,在△ABC中,AB=AC,若在腰AB上取一点D,在腰AC的延长线上也取一点F,连结DF交BC于点E,只要满足BD=CF,则DE和EF之间始终有一个固定关系,你能猜出是什么关系吗?
D
C
B
A
E
F
欧几里德-人物简介
?欧几里得 Euclid? 约公元前 325年
—公元前 265年, 古希腊数学家,以
其所著的《几何原本》(简称《原本》)闻名于曾受业于柏拉图学园。后应埃及托勒密国王邀请,在雅典移居亚历山大,从事数学教学和研究工作。他一生治学严谨。所著《几何原本》13卷,是世界上最早公理化的教学著作,影响着历代科学文化的发展和科技人才培养。牛顿数学、物理学的研究,爱因斯坦相对论的创立,都是他们精通并善于应用几何学是分不开的。
课外拓展2:
已知:如图,AB=AC,BD=CD.
求证:△ABD≌△ACD.
证明:在△ABD与△ACD中,
∴ △ABD≌△ACD( ).
AB=AC
BD=CD
AD=AD
已知
已知
公共边
SSS
复习3
隐含条件:
公共边相等
