沪教版(上海)初中数学八年级第一学期 19.2(2)证明举例 课件(19张PPT)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.2(2)证明举例 课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 865.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 17:15:39 | ||
图片预览




文档简介
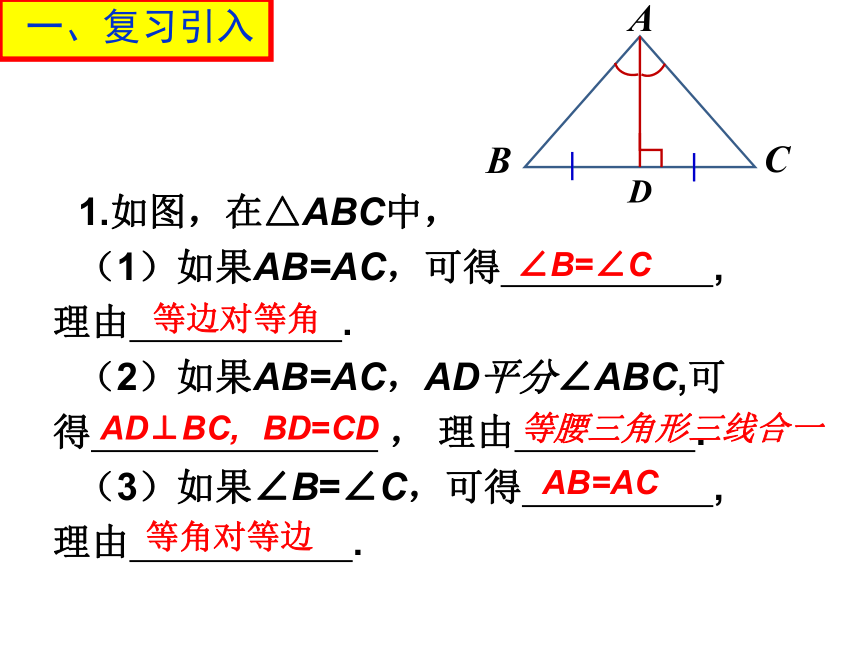
1.如图,在△ABC中,
(1)如果AB=AC,可得 ,
理由 .
(2)如果AB=AC,AD平分∠ABC,可 得 , 理由 .
(3)如果∠B=∠C,可得 ,
理由 .
∠B=∠C
等边对等角
AB=AC
等角对等边
一、复习引入
C
A
B
D
AD⊥BC,
BD=CD
等腰三角形三线合一
2.判定两个三角形全等的方法有哪些?
(S.A.S)
(A.S.A)
(A.A.S)
(S.S.S)
一、复习引入
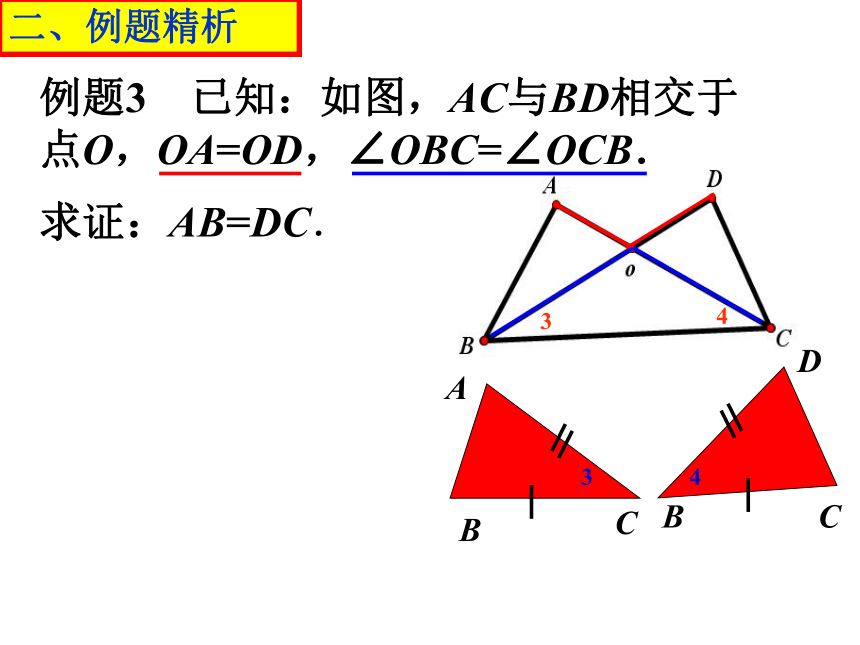
例题3 已知:如图,AC与BD相交于点O,OA=OD,∠OBC=∠OCB.
求证:AB=DC .
A
C
D
O
B
O
1
2
3
4
2
1
分析:根据题目还可以得到什么结论?
二、例题精析
例题3 已知:如图,AC与BD相交于点O,OA=OD,∠OBC=∠OCB.
求证:AB=DC.
3
4
A
B
C
C
B
D
3
4
二、例题精析
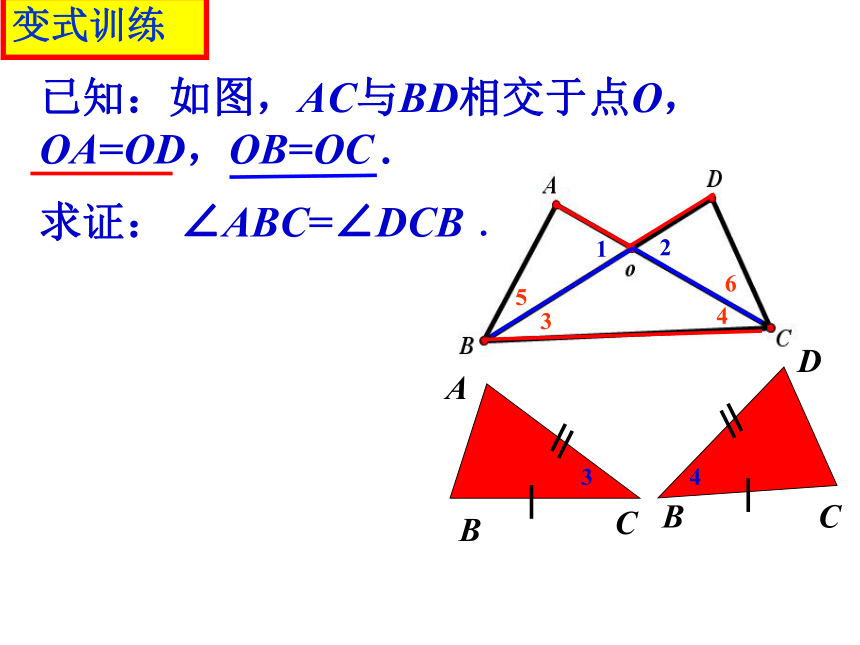
已知:如图,AC与BD相交于点O,OA=OD,OB=OC .
求证: ∠ABC=∠DCB .
3
4
变式训练
2
1
A
B
C
C
B
D
3
4
5
6
归纳:
证明线段和角相等的一般方法:
1.如果线段或角在一个三角形中,那么可用等腰三角形的判定和性质进行证明.
2.如果线段或角在两个三角形中,那么可用全等三角形的判定和性质进行证明.
3.利用线段的和差或角的和差也可以证明线段相等或角相等.
例题4 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.
D
B
A
C
问:如何证明两个角相等?
通过添加辅助线,构造全等三角形
或等腰三角形.
D
B
A
C
联结AD
△ABD≌△ACD
∠B=∠C
联结BC
AB=AC
1
3
2
4
∠1=∠2
∠3=∠4
DB=DC
∠ABD=∠ACD
注意角的表示方法
二、例题精析
例题4 已知:如图,AB=AC,DB=DC
求证:∠B=∠C.
D
B
A
C
变式训练
联结AD
△ABD≌△ACD
∠B=∠C
联结BC
AB=AC
∠ABC=∠ACB
∠DBC=∠DCB
DB=DC
∠ABD=∠ACD
SSA不能证明
两个三角形全等.
例题4 已知:如图, ,DB=DC
求证: .
D
B
A
C
变式训练
∠B=∠C
AB=AC
AB=AC
∠B=∠C
D
B
A
C
可以证明△ABD≌△ACD
吗?
1
3
4
2
联结BC
∠3=∠4
DB=DC
∠1=∠2
AB=AC
归纳
当“已知条件”与“待证结论”之间没有直接联系时,要架设沟通条件与结论的桥梁-----添置合理辅助线.
巩固练习
课本P92 练习19.2(2)
已知:如图,△ABC中,AD平分∠BAC, AD ⊥BC,
垂足为点D.
求证: △ABC 是等腰三角形.
1
2
∟
BD=CD
2.已知:如图,AB=AC,AD=AE, AB、DC相交于M ,
AC、BE相交于N,∠DAB=∠EAC.
求证:∠D=∠E.
2
1
AB=AC
∠D=∠E
已知:如图,E、F是线段BC上的两点, AB//CD,
AB=DC,CE=BF.
求证:AE=DF.
∠EAF=∠FDE
拓展练习
已知,如图,在△ABC中,AB=AC,点D为AB上的一点,点F为AC延长线上的一点, BD=CF,DF交BC于点E.你能判断出线段DE与EF有怎样的数量关系吗?如果能,请证明你的判断.
A
B
C
F
D
E
M
猜想: DE=EF
证明线段和角相等的一般方法:
1.如果线段或角在一个三角形中,那么可用等腰三
角形的判定和性质进行证明.
2.如果线段或角在两个三角形中,那么可用全等三
角形的判定和性质进行证明.
3.利用线段和差或角的和差也可以证明线段相等或
角相等.
4.当“已知条件”与“待证结论”之间没有直接联
系时,添置辅助线,构造基本图形.
三、课堂小结
四、故事了解
??欧几里得是公元前三世纪的希腊数学家,他是我们现在所学的欧氏几何的创始人,历史上称之为“几何学之父”。
?欧几里得把毕生的精力献给了科学事业。他一生刻苦钻研,治学严谨,他在科学事业上的伟大成就,正是通过自己的辛勤劳动换来的。因此,他始终反对那种不想付出辛勤劳动,而指望通过走捷径、投机取巧来取得成绩的治学态度。下面这个故事很好地反映了他的性格。
四、故事了解
??当时统治埃及的托勒密国王为了赶时髦,想学一点几何学。他自命“天赋圣明”,认为对于天下无论什么事情,他都能一看就懂,一学就会。可当他翻阅了十三卷《几何原本》之后,皱起了眉头来。他转念一想,又自作聪明地认为,这类“繁琐说教”乃是专为凡夫俗子而设的,像他这般富有的天子,肯定另有一条捷径。于是他问欧几里得:“学习几何学除了看《几何原本》之外,有没有其他的捷径?”欧几里得笑道:“陛下,很抱歉。在学习科学的时候,国王和百姓都是一样的。科学上没有专供国王走的捷径。学习几何学,人人都要独立思考,就像种庄稼一样,不耕耘就不会有收获的。”从此之后,“几何无王者之道”就成为学习数学的箴言而流传至今。
练习册习题19.2(2)
五、作业布置
(1)如果AB=AC,可得 ,
理由 .
(2)如果AB=AC,AD平分∠ABC,可 得 , 理由 .
(3)如果∠B=∠C,可得 ,
理由 .
∠B=∠C
等边对等角
AB=AC
等角对等边
一、复习引入
C
A
B
D
AD⊥BC,
BD=CD
等腰三角形三线合一
2.判定两个三角形全等的方法有哪些?
(S.A.S)
(A.S.A)
(A.A.S)
(S.S.S)
一、复习引入
例题3 已知:如图,AC与BD相交于点O,OA=OD,∠OBC=∠OCB.
求证:AB=DC .
A
C
D
O
B
O
1
2
3
4
2
1
分析:根据题目还可以得到什么结论?
二、例题精析
例题3 已知:如图,AC与BD相交于点O,OA=OD,∠OBC=∠OCB.
求证:AB=DC.
3
4
A
B
C
C
B
D
3
4
二、例题精析
已知:如图,AC与BD相交于点O,OA=OD,OB=OC .
求证: ∠ABC=∠DCB .
3
4
变式训练
2
1
A
B
C
C
B
D
3
4
5
6
归纳:
证明线段和角相等的一般方法:
1.如果线段或角在一个三角形中,那么可用等腰三角形的判定和性质进行证明.
2.如果线段或角在两个三角形中,那么可用全等三角形的判定和性质进行证明.
3.利用线段的和差或角的和差也可以证明线段相等或角相等.
例题4 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.
D
B
A
C
问:如何证明两个角相等?
通过添加辅助线,构造全等三角形
或等腰三角形.
D
B
A
C
联结AD
△ABD≌△ACD
∠B=∠C
联结BC
AB=AC
1
3
2
4
∠1=∠2
∠3=∠4
DB=DC
∠ABD=∠ACD
注意角的表示方法
二、例题精析
例题4 已知:如图,AB=AC,DB=DC
求证:∠B=∠C.
D
B
A
C
变式训练
联结AD
△ABD≌△ACD
∠B=∠C
联结BC
AB=AC
∠ABC=∠ACB
∠DBC=∠DCB
DB=DC
∠ABD=∠ACD
SSA不能证明
两个三角形全等.
例题4 已知:如图, ,DB=DC
求证: .
D
B
A
C
变式训练
∠B=∠C
AB=AC
AB=AC
∠B=∠C
D
B
A
C
可以证明△ABD≌△ACD
吗?
1
3
4
2
联结BC
∠3=∠4
DB=DC
∠1=∠2
AB=AC
归纳
当“已知条件”与“待证结论”之间没有直接联系时,要架设沟通条件与结论的桥梁-----添置合理辅助线.
巩固练习
课本P92 练习19.2(2)
已知:如图,△ABC中,AD平分∠BAC, AD ⊥BC,
垂足为点D.
求证: △ABC 是等腰三角形.
1
2
∟
BD=CD
2.已知:如图,AB=AC,AD=AE, AB、DC相交于M ,
AC、BE相交于N,∠DAB=∠EAC.
求证:∠D=∠E.
2
1
AB=AC
∠D=∠E
已知:如图,E、F是线段BC上的两点, AB//CD,
AB=DC,CE=BF.
求证:AE=DF.
∠EAF=∠FDE
拓展练习
已知,如图,在△ABC中,AB=AC,点D为AB上的一点,点F为AC延长线上的一点, BD=CF,DF交BC于点E.你能判断出线段DE与EF有怎样的数量关系吗?如果能,请证明你的判断.
A
B
C
F
D
E
M
猜想: DE=EF
证明线段和角相等的一般方法:
1.如果线段或角在一个三角形中,那么可用等腰三
角形的判定和性质进行证明.
2.如果线段或角在两个三角形中,那么可用全等三
角形的判定和性质进行证明.
3.利用线段和差或角的和差也可以证明线段相等或
角相等.
4.当“已知条件”与“待证结论”之间没有直接联
系时,添置辅助线,构造基本图形.
三、课堂小结
四、故事了解
??欧几里得是公元前三世纪的希腊数学家,他是我们现在所学的欧氏几何的创始人,历史上称之为“几何学之父”。
?欧几里得把毕生的精力献给了科学事业。他一生刻苦钻研,治学严谨,他在科学事业上的伟大成就,正是通过自己的辛勤劳动换来的。因此,他始终反对那种不想付出辛勤劳动,而指望通过走捷径、投机取巧来取得成绩的治学态度。下面这个故事很好地反映了他的性格。
四、故事了解
??当时统治埃及的托勒密国王为了赶时髦,想学一点几何学。他自命“天赋圣明”,认为对于天下无论什么事情,他都能一看就懂,一学就会。可当他翻阅了十三卷《几何原本》之后,皱起了眉头来。他转念一想,又自作聪明地认为,这类“繁琐说教”乃是专为凡夫俗子而设的,像他这般富有的天子,肯定另有一条捷径。于是他问欧几里得:“学习几何学除了看《几何原本》之外,有没有其他的捷径?”欧几里得笑道:“陛下,很抱歉。在学习科学的时候,国王和百姓都是一样的。科学上没有专供国王走的捷径。学习几何学,人人都要独立思考,就像种庄稼一样,不耕耘就不会有收获的。”从此之后,“几何无王者之道”就成为学习数学的箴言而流传至今。
练习册习题19.2(2)
五、作业布置
