沪教版(上海)初中数学八年级第一学期 19.2平行线的判定与性质 课件(共16张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.2平行线的判定与性质 课件(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 526.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 18:33:32 | ||
图片预览





文档简介
(1)∵∠BDE=∠______(已知)
∴DE∥AC
( )
(2)∵∠A+∠______=180°(已知)
∴DF∥AB ( )
(3)∵∠DFC=∠______(已知)
∴DE∥AC ( )
同位角相等,两直线平行。
C
AFD
同旁内角互补,两直线平行。
内错角相等,两直线平行。
EDF
1.填空
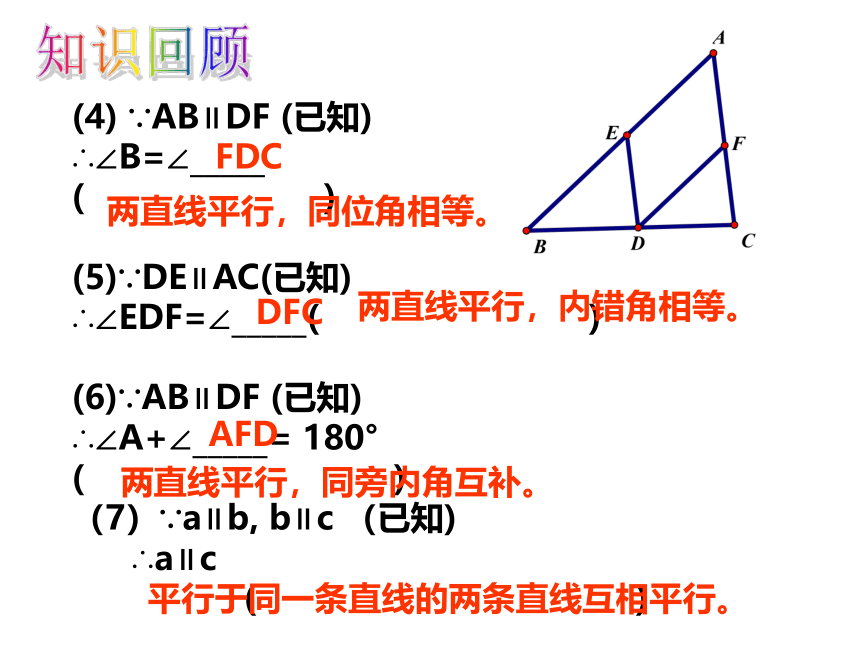
(4) ∵AB∥DF (已知)
∴∠B=∠_____
( )
(5)∵DE∥AC(已知)
∴∠EDF=∠_____( )
(6)∵AB∥DF (已知)
∴∠A+∠_____= 180°
( )
(7)∵a∥b, b∥c (已知)
∴a∥c
( )
两直线平行,同位角相等。
FDC
DFC
两直线平行,内错角相等。
AFD
两直线平行,同旁内角互补。
平行于同一条直线的两条直线互相平行。
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
(数量关系)
(位置关系)
(数量关系)
数形转化
平行线的判定与性质的关系图
判定:已知角的关系得平行的关系.证平行,用判定.
性质:已知平行的关系得角的关系.知平行,用性质.
知
识
梳
理
∠1= ∠2
∠2= ∠4
∠2+∠3=180°
a∥b
a∥b
∠1= ∠2
∠2= ∠4
∠2+ ∠3=180°
若a∥c , b ∥c,
则a∥b
1
2
3
4
a
b
c
1.如图,不能判定AB∥CD的条件是( )
A. ∠B+ ∠BCD=180° B. ∠1= ∠2
C. ∠3= ∠4 D. ∠B= ∠5
B
AD∥BC
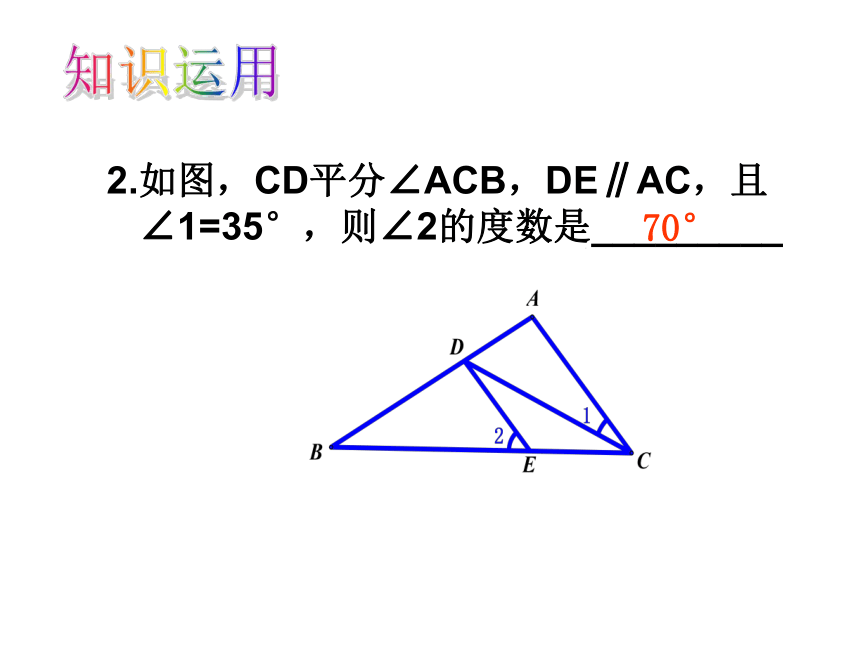
2.如图,CD平分∠ACB,DE∥AC,且∠1=35°,则∠2的度数是_________
70°
3.如图,∠1=820, ∠2=980,∠3=800,
求∠4的度数。
解 ∵ ∠1=820, ∠2=980 ( )
∴∠1+∠2= 0 ( )
又∵ +∠5=1800 ( )
∴ ∠1=∠5 ( )
∴ a//b ( )
∴ =∠4 ( )
又∵ ∠3=800 ( )
∴ ( )
a
b
c
d
1
5
2
4
3
已知
180
等式性质
∠2
邻补角的意义
同角的补角相等
同位角相等,两直线平行
∠3
两直线平行,内错角相等
已知
∠4=800
等量代换
4.如图:已知∠E=∠F ,∠A=∠C,试说明AB ∥DC.
A
E
D
F
B
C
变式:如上图请在① ∠E=∠F ,② ∠A=∠C ,
③ AB ∥ DC这三条信息中,选择其中的两条信息
作为条件,剩下的一条信息作为结论,再编制一道
不同的试题.
5.如图:AB∥CD,∠A=50°,
∠C=40°,求∠APC的度数 .
(你能用不同的方法解题吗?)
变式: 如图:AB∥CD,∠A=100°,
∠C=120°,求∠APC的度数
平行线的性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
平行线的判定:
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
平行线的判定,性质
平行于同一条直线的两条直线互相平行。
如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
(你可以用不同的方法解本题吗?)
?
?
如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
M
N
如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
O
如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
O
∴DE∥AC
( )
(2)∵∠A+∠______=180°(已知)
∴DF∥AB ( )
(3)∵∠DFC=∠______(已知)
∴DE∥AC ( )
同位角相等,两直线平行。
C
AFD
同旁内角互补,两直线平行。
内错角相等,两直线平行。
EDF
1.填空
(4) ∵AB∥DF (已知)
∴∠B=∠_____
( )
(5)∵DE∥AC(已知)
∴∠EDF=∠_____( )
(6)∵AB∥DF (已知)
∴∠A+∠_____= 180°
( )
(7)∵a∥b, b∥c (已知)
∴a∥c
( )
两直线平行,同位角相等。
FDC
DFC
两直线平行,内错角相等。
AFD
两直线平行,同旁内角互补。
平行于同一条直线的两条直线互相平行。
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
(数量关系)
(位置关系)
(数量关系)
数形转化
平行线的判定与性质的关系图
判定:已知角的关系得平行的关系.证平行,用判定.
性质:已知平行的关系得角的关系.知平行,用性质.
知
识
梳
理
∠1= ∠2
∠2= ∠4
∠2+∠3=180°
a∥b
a∥b
∠1= ∠2
∠2= ∠4
∠2+ ∠3=180°
若a∥c , b ∥c,
则a∥b
1
2
3
4
a
b
c
1.如图,不能判定AB∥CD的条件是( )
A. ∠B+ ∠BCD=180° B. ∠1= ∠2
C. ∠3= ∠4 D. ∠B= ∠5
B
AD∥BC
2.如图,CD平分∠ACB,DE∥AC,且∠1=35°,则∠2的度数是_________
70°
3.如图,∠1=820, ∠2=980,∠3=800,
求∠4的度数。
解 ∵ ∠1=820, ∠2=980 ( )
∴∠1+∠2= 0 ( )
又∵ +∠5=1800 ( )
∴ ∠1=∠5 ( )
∴ a//b ( )
∴ =∠4 ( )
又∵ ∠3=800 ( )
∴ ( )
a
b
c
d
1
5
2
4
3
已知
180
等式性质
∠2
邻补角的意义
同角的补角相等
同位角相等,两直线平行
∠3
两直线平行,内错角相等
已知
∠4=800
等量代换
4.如图:已知∠E=∠F ,∠A=∠C,试说明AB ∥DC.
A
E
D
F
B
C
变式:如上图请在① ∠E=∠F ,② ∠A=∠C ,
③ AB ∥ DC这三条信息中,选择其中的两条信息
作为条件,剩下的一条信息作为结论,再编制一道
不同的试题.
5.如图:AB∥CD,∠A=50°,
∠C=40°,求∠APC的度数 .
(你能用不同的方法解题吗?)
变式: 如图:AB∥CD,∠A=100°,
∠C=120°,求∠APC的度数
平行线的性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
平行线的判定:
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
平行线的判定,性质
平行于同一条直线的两条直线互相平行。
如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
(你可以用不同的方法解本题吗?)
?
?
如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
M
N
如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
O
如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
O
