沪教版(上海)初中数学八年级第一学期 19.4 线段的垂直平分线 课件(共25张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.4 线段的垂直平分线 课件(共25张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 696.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 18:29:43 | ||
图片预览








文档简介
实际问题1
计划在张杨路附近建立一个大型的图书馆.试问,该图书馆应建于何处,才能使得它到“建平中学”和“建平实验”两个学校的距离相等?
张 杨 路
19.4 线段的垂直平分线
A
B
PA=PB
P1A=P1B
……
命题:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
M
N
作线段AB的垂直平分线MN,垂足为C
由此你能得到什么规律?
PA、PB有什么数量关系?
CA=CB
P
P1
C
∟
在MN上任取一点P,联结PA、PB;
如图, 直线MN垂直平分AB,垂
足为C, 点P直线MN上
命题:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
A
B
P
M
N
C
PA=PB
已知:
求证:
证明:∵直线MN垂直平分AB(已知)
∴ ∠ PCA= ∠ PCB=90o AC=BC
(垂直平分线的定义)
在 ΔPAC和ΔPBC中,
AC=BC (已证)
∠ PCA= ∠ PCB (已证)
PC=PC (公共边)
∴ ΔPAC ≌Δ PBC(S.A.S)
∴PA=PB(全等三角形的对应边相等)
如果点P在C点, 结论成立吗?
定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
A
B
P
M
N
C
∵点P在线段AB的垂直平分线上 (已知)
∴PA=PB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)
例题1 已知:如图,△ABC中, AB= AC= 8 , AB的垂直平分线MN分别交 AB于D,交 AC于E, BC = 3 .求:
△BEC的周长.
∵点P在线段AB的垂直平分线上 (已知)
∴PA=PB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)
你能把这个命题的逆命题写出来吗?
A
B
P
M
N
定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
A
B
P
C
定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
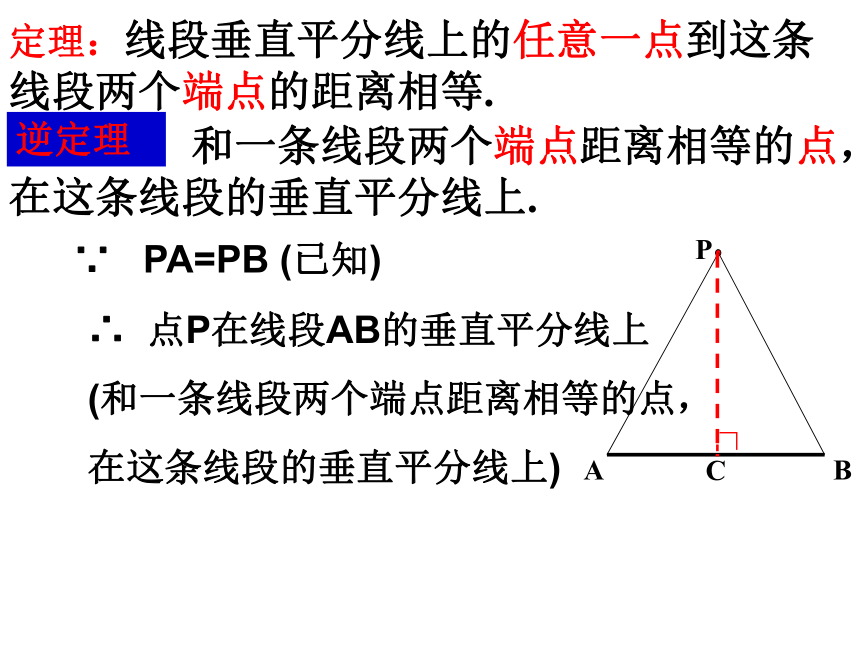
逆命题: 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
已知:PA=PB
求证:点P在线段AB的垂直平分线上
∟
如果点P在C点, 结论成立吗?
逆定理
A
B
P
C
定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
逆命题: 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∟
∴ 点P在线段AB的垂直平分线上
(和一条线段两个端点距离相等的点,
在这条线段的垂直平分线上)
逆定理
∵ PA=PB (已知)
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是
的所有点的集合.
和线段两个端点距离相等
A
B
P
M
N
C
1、如下图直线MN垂直平分线段AB,则AD=AE.
判断题
M
N
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
2、如图线段MN被直线AB垂直平分,则ME=NE.
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
A
B
3、如图EM=EN,则直线AB是线段MN的垂直平分线.
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
A
B
3、如图EM=EN,则直线AB是线段MN的垂直平分线.
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
A
B
4、若MA=MB,NA=NB,则MN垂直平分AB.
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
例2 已知:如图,在ΔABC中,边AB,BC的垂直平分线PM、PN交于P.
求证:
点P在AC的垂直平分线上
证明: 联结PA、PB、PC
∵ 点P在边AB的垂直平分线上(已知)
∴PA=PB
(线段垂直平分线上的任意一点到这条线段两端的距离相等)
同理:PB=PC
∴ PA=PC(等量代换)
∴ 点P在线段AC的垂直平分线上
(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
实际问题1
计划在张杨路附近建立一个大型的图书馆.试问,该图书馆应建于何处,才能使得它到“建平中学”和“建平实验”两个学校的距离相等?
张 杨 路
建平中学
建平实验
实际问题
数学问题
A
B
l
如图,在直线 l
上求作一点P,
使PA=PB.
P
·
实际问题2
计划在建平中学、建平实验、进才中学之间建立一个大型的图书馆. 试问,该图书馆应建于何处,才能使得它到三个学校的距离相等?
B
A
C
求作一点P,使它和△ABC的三个顶点距离相等.
实际问题
数学问题
p
PA=PB=PC
实际问题3
计划在张杨路附近建立一个大型的图书馆. 试问,该图书馆应建于何处,才能使得它到“建平中学”和“建平实验” 的距离之和最短?
张 杨 路
拓 展:
谈谈你这节课的收获……
作业
练习册 19.4
从军行——唐 李维
白日登山望烽火,
黄昏饮马傍交河。
从军行——唐 李维
白日登山望烽火,
黄昏饮马傍交河。
营地A
观望台B
河
P饮马地点
计划在张杨路附近建立一个大型的图书馆.试问,该图书馆应建于何处,才能使得它到“建平中学”和“建平实验”两个学校的距离相等?
张 杨 路
19.4 线段的垂直平分线
A
B
PA=PB
P1A=P1B
……
命题:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
M
N
作线段AB的垂直平分线MN,垂足为C
由此你能得到什么规律?
PA、PB有什么数量关系?
CA=CB
P
P1
C
∟
在MN上任取一点P,联结PA、PB;
如图, 直线MN垂直平分AB,垂
足为C, 点P直线MN上
命题:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
A
B
P
M
N
C
PA=PB
已知:
求证:
证明:∵直线MN垂直平分AB(已知)
∴ ∠ PCA= ∠ PCB=90o AC=BC
(垂直平分线的定义)
在 ΔPAC和ΔPBC中,
AC=BC (已证)
∠ PCA= ∠ PCB (已证)
PC=PC (公共边)
∴ ΔPAC ≌Δ PBC(S.A.S)
∴PA=PB(全等三角形的对应边相等)
如果点P在C点, 结论成立吗?
定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
A
B
P
M
N
C
∵点P在线段AB的垂直平分线上 (已知)
∴PA=PB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)
例题1 已知:如图,△ABC中, AB= AC= 8 , AB的垂直平分线MN分别交 AB于D,交 AC于E, BC = 3 .求:
△BEC的周长.
∵点P在线段AB的垂直平分线上 (已知)
∴PA=PB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)
你能把这个命题的逆命题写出来吗?
A
B
P
M
N
定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
A
B
P
C
定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
逆命题: 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
已知:PA=PB
求证:点P在线段AB的垂直平分线上
∟
如果点P在C点, 结论成立吗?
逆定理
A
B
P
C
定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
逆命题: 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∟
∴ 点P在线段AB的垂直平分线上
(和一条线段两个端点距离相等的点,
在这条线段的垂直平分线上)
逆定理
∵ PA=PB (已知)
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是
的所有点的集合.
和线段两个端点距离相等
A
B
P
M
N
C
1、如下图直线MN垂直平分线段AB,则AD=AE.
判断题
M
N
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
2、如图线段MN被直线AB垂直平分,则ME=NE.
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
A
B
3、如图EM=EN,则直线AB是线段MN的垂直平分线.
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
A
B
3、如图EM=EN,则直线AB是线段MN的垂直平分线.
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
A
B
4、若MA=MB,NA=NB,则MN垂直平分AB.
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
例2 已知:如图,在ΔABC中,边AB,BC的垂直平分线PM、PN交于P.
求证:
点P在AC的垂直平分线上
证明: 联结PA、PB、PC
∵ 点P在边AB的垂直平分线上(已知)
∴PA=PB
(线段垂直平分线上的任意一点到这条线段两端的距离相等)
同理:PB=PC
∴ PA=PC(等量代换)
∴ 点P在线段AC的垂直平分线上
(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
实际问题1
计划在张杨路附近建立一个大型的图书馆.试问,该图书馆应建于何处,才能使得它到“建平中学”和“建平实验”两个学校的距离相等?
张 杨 路
建平中学
建平实验
实际问题
数学问题
A
B
l
如图,在直线 l
上求作一点P,
使PA=PB.
P
·
实际问题2
计划在建平中学、建平实验、进才中学之间建立一个大型的图书馆. 试问,该图书馆应建于何处,才能使得它到三个学校的距离相等?
B
A
C
求作一点P,使它和△ABC的三个顶点距离相等.
实际问题
数学问题
p
PA=PB=PC
实际问题3
计划在张杨路附近建立一个大型的图书馆. 试问,该图书馆应建于何处,才能使得它到“建平中学”和“建平实验” 的距离之和最短?
张 杨 路
拓 展:
谈谈你这节课的收获……
作业
练习册 19.4
从军行——唐 李维
白日登山望烽火,
黄昏饮马傍交河。
从军行——唐 李维
白日登山望烽火,
黄昏饮马傍交河。
营地A
观望台B
河
P饮马地点
