沪教版(上海)初中数学八年级第一学期 19.4线段的垂直平分线 课件 (1)(17张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.4线段的垂直平分线 课件 (1)(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 880.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览




文档简介
如果一个点在一条线段的垂直平分线上,那么分别联结这点与线段两个端点所得的两条线段相等.
学习新知
1、画图,2、写已知,求证,3、证明.
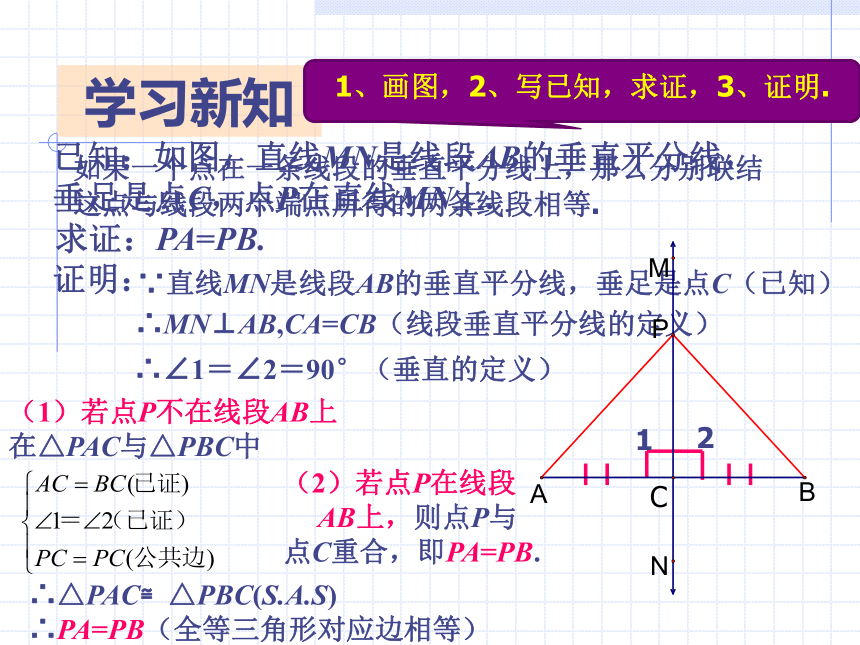
已知:如图,直线MN是线段AB的垂直平分线,
垂足是点C,点P在直线MN上.
求证:PA=PB.
证明:
∵直线MN是线段AB的垂直平分线,垂足是点C(已知)
∴MN⊥AB,CA=CB(线段垂直平分线的定义)
∴∠1=∠2=90°(垂直的定义)
(1)若点P不在线段AB上
在△PAC与△PBC中
∴△PAC≌△PBC(S.A.S)
∴PA=PB(全等三角形对应边相等)
(2)若点P在线段
AB上,则点P与
点C重合,即PA=PB.
1
2
C
B
A
M
N
P
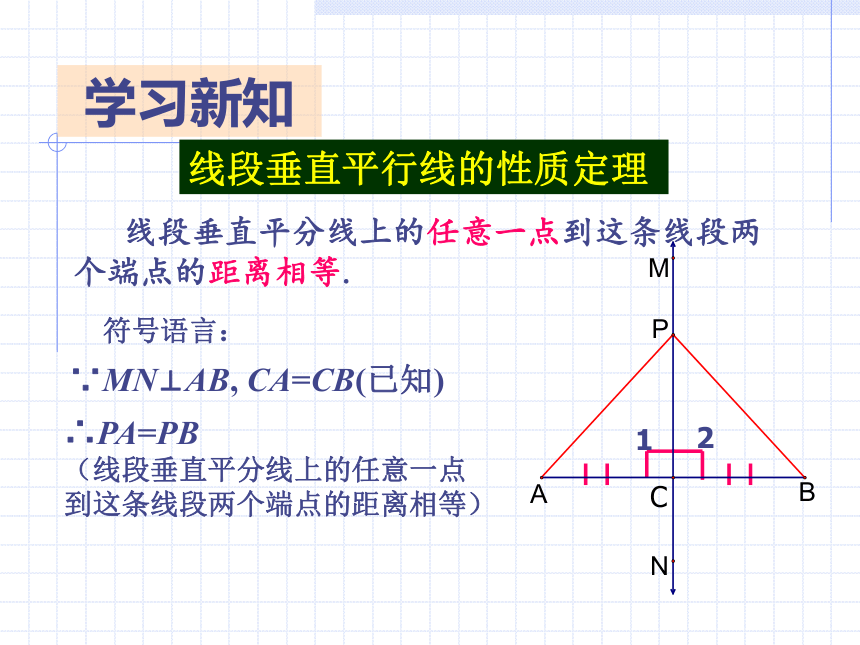
线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
学习新知
线段垂直平行线的性质定理
∵MN⊥AB, CA=CB(已知)
∴PA=PB
(线段垂直平分线上的任意一点
到这条线段两个端点的距离相等)
1
2
C
B
A
M
N
P
符号语言:
学习新知
线段垂直平行线的性质定理
线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
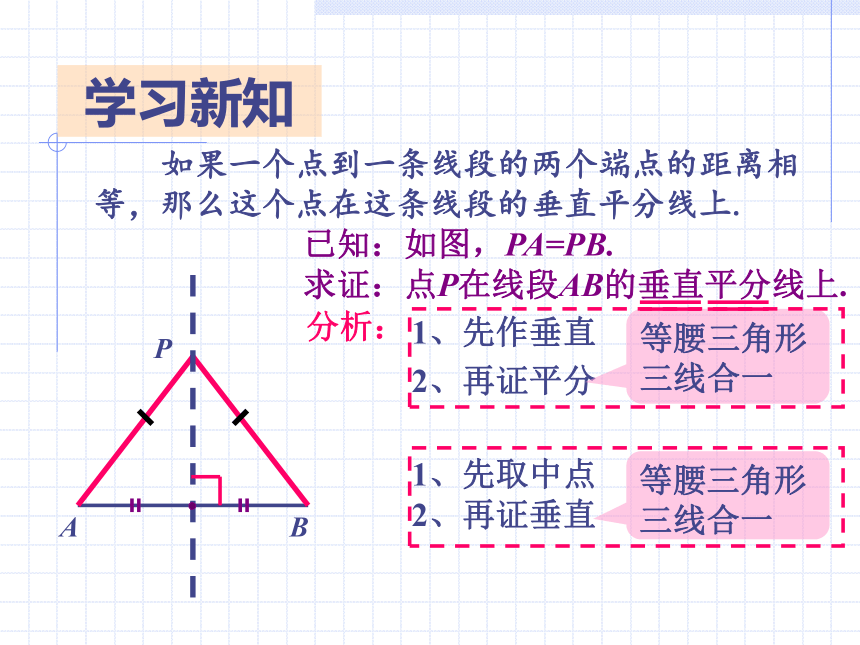
如果一个点到一条线段的两个端点的距离相
等,那么这个点在这条线段的垂直平分线上.
逆命题
学习新知
如果一个点到一条线段的两个端点的距离相
等,那么这个点在这条线段的垂直平分线上.
学习新知
如果一个点到一条线段的两个端点的距离相
等,那么这个点在这条线段的垂直平分线上.
A
B
P
已知:如图,PA=PB.
求证:点P在线段AB的垂直平分线上.
分析:
1、先作垂直
2、再证平分
等腰三角形三线合一
1、先取中点
2、再证垂直
等腰三角形三线合一
学习新知
如果一个点到一条线段的两个端点的距离相等,
那么这个点在这条线段的垂直平分线上.
已知:如图,PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:
(1)如果点P在线段AB上,那么点P就是线段AB的中点,即在线段AB的垂直平分线上.
A
B
P
(2)如果点P不在线段AB上,过点P作PD⊥AB,垂足为点D.
∵PA=PB(已知),PD⊥AB(已作).
D
∴AD=BD(等腰三角形三线合一).
∴点P在线段AB的垂直平分线上.
学习新知
线段垂直平行线的性质定理的逆定理
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
符号语言:
∵AB=AC(已知)
∴点A在线段BC的垂直平分线上
(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
图形语言:
过点A的直线一定是已知线段的垂直平分线吗?
学习新知
任何图形都是由点组成的,因此我们可以把图形看成点的集合.
组成线段BC的垂直平分线的所有点和B、C两点的距离都相等;
线段的垂直平分线可以看作是和这条线段两个端点的距离相等的点的集合.
反过来,和B、C两点距离相等的所有的点组成线段AB的垂直平分线.
B
C
综合运用
例1、已知:如图,AB=AC,DB=DC,点E是直线AD上一点.
求证:BE=CE.
证明:
∵AB=AC(已知)
∴点A在线段BC的垂直平分线上
(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
∴BE=CE(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)
同理点D也在线段BC的垂直平分线上
∴直线AD是线段BC的垂直平分线
综合运用
例2、已知:如图,在△ABC中,OM、ON分别是AB、AC的垂直平分线,OM与ON相交与点O.
求证:点O在BC的垂直平分线上.
M
N
O
C
B
A
OA=OB
OA=OC
OB=OC
M
N
O
C
B
A
综合运用
例2、已知:如图,在△ABC中,OM、ON分别是AB、AC的垂直平分线,OM与ON相交与点O.
求证:点O在BC的垂直平分线上.
证明:分别联结OB、OA、OC.
∵OM是AB的垂直平分线(已知)
∴OA=OB
(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)
同理,OA=OC.
∴OB=OC(等量代换)
∴点O在BC的垂直平分线上
(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
三角形的三条边的垂直平分线交于一点,且这点到三个顶点的距离相等.
适时小结
C
B
A
M
N
C
B
A
M
N
P
性质定理
点A在线段BC的
垂直平分线上
逆定理
课堂练习
(1)如图,已知在△ABC中, AB= AC=12cm,AB的垂直平分线分别交AB、 AC于点E、D ,且△BCD的周长为17cm,求底边BC的长.
A
D
E
C
B
解:∵ED是AC的垂直平分线(已知),
∴AD=DB
(线段垂直平分线上的任意一点到这
条线段两个端点的距离相等).
∴AC=AD+DC=BD+CD(等量代换).
∵C △BCD =BD+DC+BC=17cm(已知),
又∵ AC= 12cm (已知),
∴BC=5cm(等式性质) .
课堂练习
(1)已知,如图,CD垂直平分AB, AB平分∠CAD.求证:AD∥BC.
解:∵CD是AB的垂直平分线(已知),
∴CA=CB
(线段垂直平分线上的任意一点
到这条线段两个端点的距离相等).
A
D
C
B
1
2
∴ ∠1= ∠B(等边对等角)
∵ AB平分∠CAD (已知),
∴ ∠ 1= ∠2(角的平分线的意义).
∴ ∠ 2= ∠B(等量代换).
∴ AD∥BC
(内错角相等,两直线平行).
课堂小结
线段垂直平行线的性质定理
线段垂直平行线的性质定理逆定理
C
B
A
M
N
C
B
A
M
N
P
点A在线段BC的
垂直平分线上
已知垂直平分线
已知线段相等
布置作业
练习册19.4
书本课后练习P105.3
学习新知
1、画图,2、写已知,求证,3、证明.
已知:如图,直线MN是线段AB的垂直平分线,
垂足是点C,点P在直线MN上.
求证:PA=PB.
证明:
∵直线MN是线段AB的垂直平分线,垂足是点C(已知)
∴MN⊥AB,CA=CB(线段垂直平分线的定义)
∴∠1=∠2=90°(垂直的定义)
(1)若点P不在线段AB上
在△PAC与△PBC中
∴△PAC≌△PBC(S.A.S)
∴PA=PB(全等三角形对应边相等)
(2)若点P在线段
AB上,则点P与
点C重合,即PA=PB.
1
2
C
B
A
M
N
P
线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
学习新知
线段垂直平行线的性质定理
∵MN⊥AB, CA=CB(已知)
∴PA=PB
(线段垂直平分线上的任意一点
到这条线段两个端点的距离相等)
1
2
C
B
A
M
N
P
符号语言:
学习新知
线段垂直平行线的性质定理
线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
如果一个点到一条线段的两个端点的距离相
等,那么这个点在这条线段的垂直平分线上.
逆命题
学习新知
如果一个点到一条线段的两个端点的距离相
等,那么这个点在这条线段的垂直平分线上.
学习新知
如果一个点到一条线段的两个端点的距离相
等,那么这个点在这条线段的垂直平分线上.
A
B
P
已知:如图,PA=PB.
求证:点P在线段AB的垂直平分线上.
分析:
1、先作垂直
2、再证平分
等腰三角形三线合一
1、先取中点
2、再证垂直
等腰三角形三线合一
学习新知
如果一个点到一条线段的两个端点的距离相等,
那么这个点在这条线段的垂直平分线上.
已知:如图,PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:
(1)如果点P在线段AB上,那么点P就是线段AB的中点,即在线段AB的垂直平分线上.
A
B
P
(2)如果点P不在线段AB上,过点P作PD⊥AB,垂足为点D.
∵PA=PB(已知),PD⊥AB(已作).
D
∴AD=BD(等腰三角形三线合一).
∴点P在线段AB的垂直平分线上.
学习新知
线段垂直平行线的性质定理的逆定理
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
符号语言:
∵AB=AC(已知)
∴点A在线段BC的垂直平分线上
(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
图形语言:
过点A的直线一定是已知线段的垂直平分线吗?
学习新知
任何图形都是由点组成的,因此我们可以把图形看成点的集合.
组成线段BC的垂直平分线的所有点和B、C两点的距离都相等;
线段的垂直平分线可以看作是和这条线段两个端点的距离相等的点的集合.
反过来,和B、C两点距离相等的所有的点组成线段AB的垂直平分线.
B
C
综合运用
例1、已知:如图,AB=AC,DB=DC,点E是直线AD上一点.
求证:BE=CE.
证明:
∵AB=AC(已知)
∴点A在线段BC的垂直平分线上
(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
∴BE=CE(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)
同理点D也在线段BC的垂直平分线上
∴直线AD是线段BC的垂直平分线
综合运用
例2、已知:如图,在△ABC中,OM、ON分别是AB、AC的垂直平分线,OM与ON相交与点O.
求证:点O在BC的垂直平分线上.
M
N
O
C
B
A
OA=OB
OA=OC
OB=OC
M
N
O
C
B
A
综合运用
例2、已知:如图,在△ABC中,OM、ON分别是AB、AC的垂直平分线,OM与ON相交与点O.
求证:点O在BC的垂直平分线上.
证明:分别联结OB、OA、OC.
∵OM是AB的垂直平分线(已知)
∴OA=OB
(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)
同理,OA=OC.
∴OB=OC(等量代换)
∴点O在BC的垂直平分线上
(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
三角形的三条边的垂直平分线交于一点,且这点到三个顶点的距离相等.
适时小结
C
B
A
M
N
C
B
A
M
N
P
性质定理
点A在线段BC的
垂直平分线上
逆定理
课堂练习
(1)如图,已知在△ABC中, AB= AC=12cm,AB的垂直平分线分别交AB、 AC于点E、D ,且△BCD的周长为17cm,求底边BC的长.
A
D
E
C
B
解:∵ED是AC的垂直平分线(已知),
∴AD=DB
(线段垂直平分线上的任意一点到这
条线段两个端点的距离相等).
∴AC=AD+DC=BD+CD(等量代换).
∵C △BCD =BD+DC+BC=17cm(已知),
又∵ AC= 12cm (已知),
∴BC=5cm(等式性质) .
课堂练习
(1)已知,如图,CD垂直平分AB, AB平分∠CAD.求证:AD∥BC.
解:∵CD是AB的垂直平分线(已知),
∴CA=CB
(线段垂直平分线上的任意一点
到这条线段两个端点的距离相等).
A
D
C
B
1
2
∴ ∠1= ∠B(等边对等角)
∵ AB平分∠CAD (已知),
∴ ∠ 1= ∠2(角的平分线的意义).
∴ ∠ 2= ∠B(等量代换).
∴ AD∥BC
(内错角相等,两直线平行).
课堂小结
线段垂直平行线的性质定理
线段垂直平行线的性质定理逆定理
C
B
A
M
N
C
B
A
M
N
P
点A在线段BC的
垂直平分线上
已知垂直平分线
已知线段相等
布置作业
练习册19.4
书本课后练习P105.3
