19.10 两点的距离公式 课件(共13张PPT)
文档属性
| 名称 | 19.10 两点的距离公式 课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 20:22:26 | ||
图片预览




文档简介
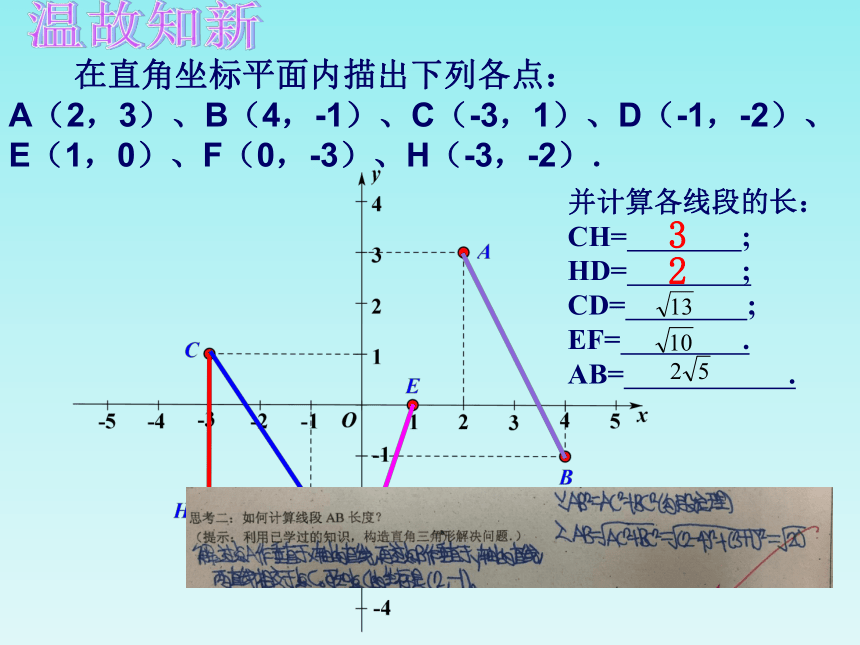
在直角坐标平面内描出下列各点:
A(2,3)、B(4,-1)、C(-3,1)、D(-1,-2)、E(1,0)、F(0,-3)、H(-3,-2).
并计算各线段的长:
CH= ;
HD= ;
CD= ;
EF= .
AB= .
3
2
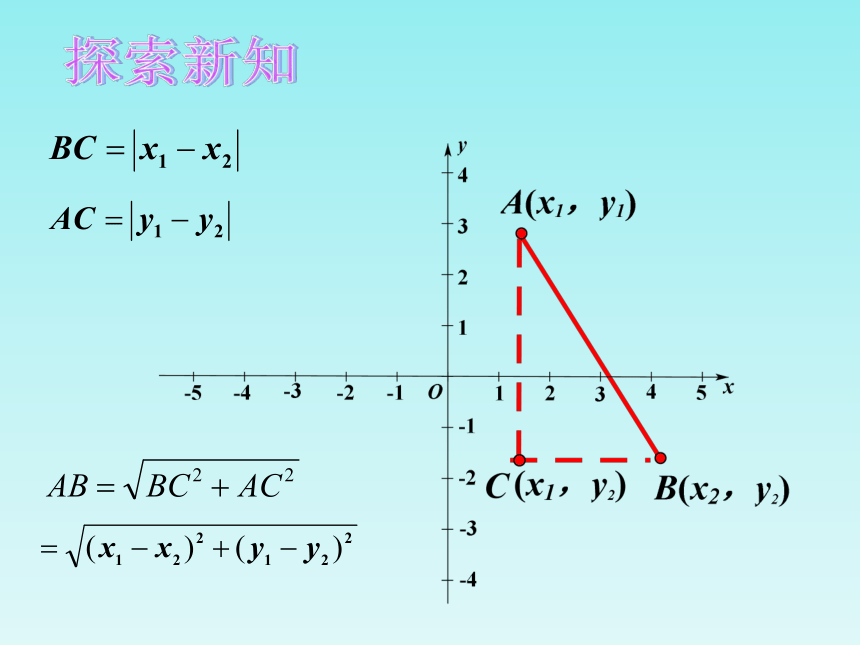
在直角坐标平面内,
两点间的距离公式:
例题1 已知直角坐标平面内A、B的两点的坐标分别为A(-3,2),B(1,-1). 求A、B两点的距离.
例题1 已知直角坐标平面内A、B的两点的坐标分别为A(-3,2),B(1,-1). 求A、B两点的距离.
练一练 A组1、求下列两点的距离:
(2) C (-3,5) D (4,-2)
(3) E(-5,0) F(-3,-4)
(1) A(0,0) B(-3,-4)
例题2 已知直角坐标平面内三个点A、B、C的坐标分别为(-1,4)、(-4,-2)、(2,-5).试判断以A、B、C为顶点的△ABC的形状.
A
B
-5
C
例题2 已知直角坐标平面内三个点A、B、C的坐标分别为(-1,4)、(-4,-2)、(2,-5).试判断以A、B、C为顶点的△ABC的形状.
在直角坐标平面内判断三角形的形状:
第一步:利用两点的距离公式求出三角形的三边的长度;
第二步:依据三角形分类的标准来判断三角形的形状.
A
B
-5
C
例题3
已知直角坐标平面内,点A在坐标轴上,且到点B(4,1)的距离为5.求点A坐标.
坐标轴
到点B(4,1)的距离为5
小组讨论:
1、坐标轴上的点有何特征?
2、符合题意的点A有多少个?
并把符合题意的点A画出来。
3、如何求点A的坐标?
1、直角坐标平面内两点A(x1,y1)、B(x2,y2)的距离公式
2、在直角坐标平面内判断三角形的形状。
回家作业:1、达标反馈B组 2、练习册19.10
3、达标反馈C组选做
A(2,3)、B(4,-1)、C(-3,1)、D(-1,-2)、E(1,0)、F(0,-3)、H(-3,-2).
并计算各线段的长:
CH= ;
HD= ;
CD= ;
EF= .
AB= .
3
2
在直角坐标平面内,
两点间的距离公式:
例题1 已知直角坐标平面内A、B的两点的坐标分别为A(-3,2),B(1,-1). 求A、B两点的距离.
例题1 已知直角坐标平面内A、B的两点的坐标分别为A(-3,2),B(1,-1). 求A、B两点的距离.
练一练 A组1、求下列两点的距离:
(2) C (-3,5) D (4,-2)
(3) E(-5,0) F(-3,-4)
(1) A(0,0) B(-3,-4)
例题2 已知直角坐标平面内三个点A、B、C的坐标分别为(-1,4)、(-4,-2)、(2,-5).试判断以A、B、C为顶点的△ABC的形状.
A
B
-5
C
例题2 已知直角坐标平面内三个点A、B、C的坐标分别为(-1,4)、(-4,-2)、(2,-5).试判断以A、B、C为顶点的△ABC的形状.
在直角坐标平面内判断三角形的形状:
第一步:利用两点的距离公式求出三角形的三边的长度;
第二步:依据三角形分类的标准来判断三角形的形状.
A
B
-5
C
例题3
已知直角坐标平面内,点A在坐标轴上,且到点B(4,1)的距离为5.求点A坐标.
坐标轴
到点B(4,1)的距离为5
小组讨论:
1、坐标轴上的点有何特征?
2、符合题意的点A有多少个?
并把符合题意的点A画出来。
3、如何求点A的坐标?
1、直角坐标平面内两点A(x1,y1)、B(x2,y2)的距离公式
2、在直角坐标平面内判断三角形的形状。
回家作业:1、达标反馈B组 2、练习册19.10
3、达标反馈C组选做
