沪教版(上海)初中数学八年级第一学期 本章小结 直角三角形复习 课件(共13张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 本章小结 直角三角形复习 课件(共13张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 438.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 19:00:17 | ||
图片预览




文档简介
直角三角形复习
教学目标:
1、掌握直角三角形的性质定理和判定定理,并会简单应用。
2、掌握直角三角形全等的判定定理并会简单的应用。
一、直角三角形的性质:
知识点回顾
直角三角形:有一个角是直角的三角形
1.直角三角形的两个锐角互余;
2.直角三角形斜边上的中线等于斜边的一半;
4.直角三角形两条直角边的平方和等于斜边的平方;
(勾股定理)
3.直角三角形中,30O角所对直角边是斜边的一半;
熟记以下几组勾股数: 3、4、5; 5、12、13;
7、24、25;8、15、17
二、直角三角形的判定:
1.定义:有一个角是直角的三角形是直角三角形
2. 有两个角是互余的三角形是直角三角形
3. 若三角形中,较小两边的平方和等于较大边的平方,
则这个三角形是直角三角形(勾股定理的逆定理)
三、直角三角形全等的判定:
AAS、ASA、SAS、SSS、HL
斜边和一条直角边对应相等的两个直角三角形全等.
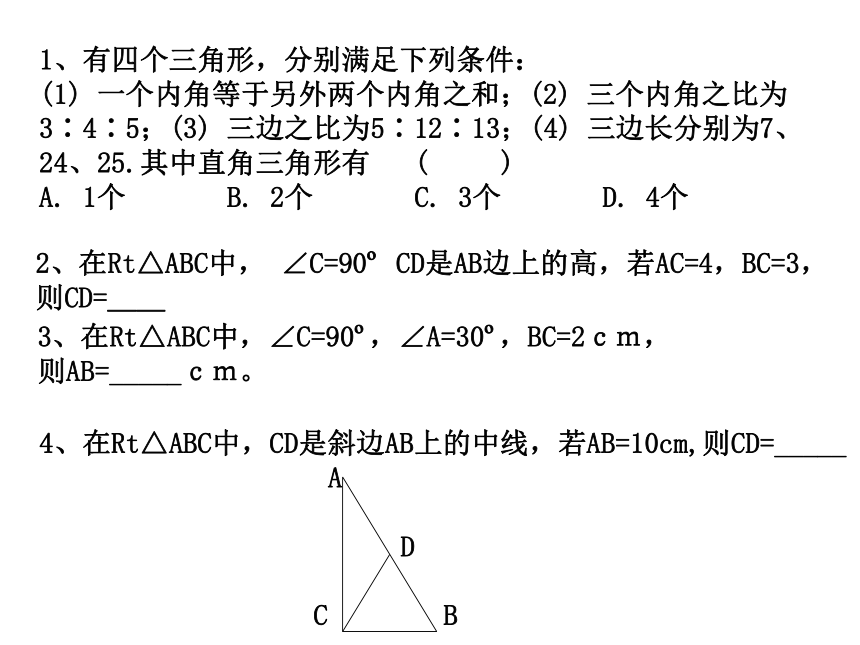
1、有四个三角形,分别满足下列条件:
(1) 一个内角等于另外两个内角之和;(2) 三个内角之比为3∶4∶5;(3) 三边之比为5∶12∶13;(4) 三边长分别为7、24、25.其中直角三角形有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
2、在Rt△ABC中, ∠C=90? CD是AB边上的高,若AC=4,BC=3,则CD=__
3、在Rt△ABC中,∠C=90?,∠A=30?,BC=2cm,
则AB=_____cm。
4、在Rt△ABC中,CD是斜边AB上的中线,若AB=10cm,则CD=_____
A
D
C B
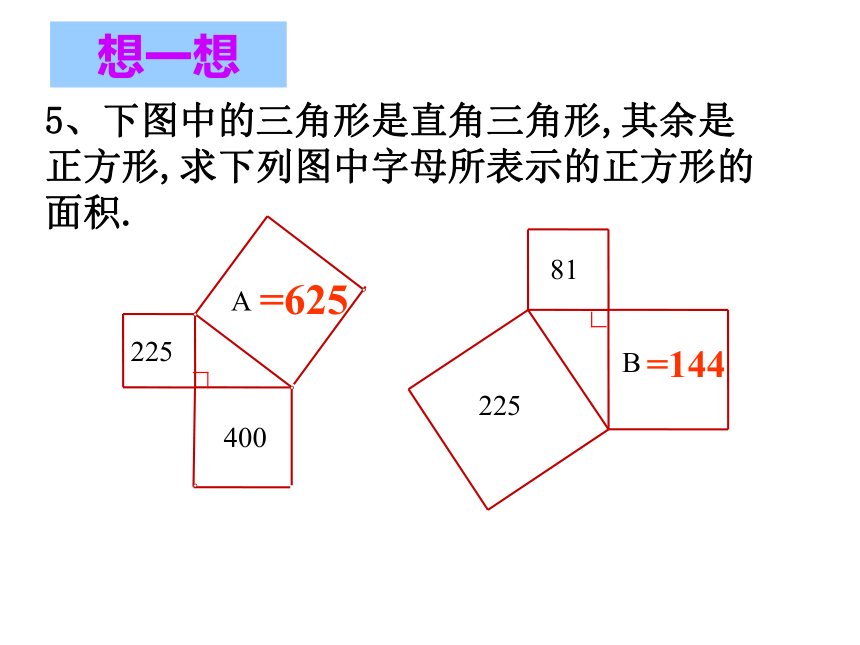
5、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
想一想
A
B
C
D
7cm
6.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
例1.已知:如图, ∠A=90°,∠B=15°,BD=DC.
请说明AC= BD的理由.
解∵BD=DC,∠B=15°
∴∠DCB=∠B=15°
(在同一三角形中,等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC=DC/2(直角三角形中,30O角所对直角边是斜边的一半)
∴AC=BD/2
例2、已知,如图,在△ABC中,D是BC边上一点,DE ⊥AB于点E,DF ⊥AC于点F,且DE=DF,EF与AD交于点O.求证;AD ⊥EF.
A
E O F
B C
D
例3:如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。
说明两条线段相等,有时还可以通过第三条线段进行等量代换。
变式题:如图,已知AD、BE分别是△ABC的BC、AC边上的高,F是DE的中点,G是AB的中点,则FG⊥DE,请说明理由。
F
E
D
C
B
A
例4:如图:AD是△ABC中BC边上的高,E为AC上一点,BE交AD于F,BF=AC,FD=CD,问BE,AC互相垂直么?请说明理由
例4、如图,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,且AP=PC,AP⊥PC,则△ABP≌△PDC,请说明理由。
教学目标:
1、掌握直角三角形的性质定理和判定定理,并会简单应用。
2、掌握直角三角形全等的判定定理并会简单的应用。
一、直角三角形的性质:
知识点回顾
直角三角形:有一个角是直角的三角形
1.直角三角形的两个锐角互余;
2.直角三角形斜边上的中线等于斜边的一半;
4.直角三角形两条直角边的平方和等于斜边的平方;
(勾股定理)
3.直角三角形中,30O角所对直角边是斜边的一半;
熟记以下几组勾股数: 3、4、5; 5、12、13;
7、24、25;8、15、17
二、直角三角形的判定:
1.定义:有一个角是直角的三角形是直角三角形
2. 有两个角是互余的三角形是直角三角形
3. 若三角形中,较小两边的平方和等于较大边的平方,
则这个三角形是直角三角形(勾股定理的逆定理)
三、直角三角形全等的判定:
AAS、ASA、SAS、SSS、HL
斜边和一条直角边对应相等的两个直角三角形全等.
1、有四个三角形,分别满足下列条件:
(1) 一个内角等于另外两个内角之和;(2) 三个内角之比为3∶4∶5;(3) 三边之比为5∶12∶13;(4) 三边长分别为7、24、25.其中直角三角形有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
2、在Rt△ABC中, ∠C=90? CD是AB边上的高,若AC=4,BC=3,则CD=__
3、在Rt△ABC中,∠C=90?,∠A=30?,BC=2cm,
则AB=_____cm。
4、在Rt△ABC中,CD是斜边AB上的中线,若AB=10cm,则CD=_____
A
D
C B
5、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
想一想
A
B
C
D
7cm
6.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
例1.已知:如图, ∠A=90°,∠B=15°,BD=DC.
请说明AC= BD的理由.
解∵BD=DC,∠B=15°
∴∠DCB=∠B=15°
(在同一三角形中,等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC=DC/2(直角三角形中,30O角所对直角边是斜边的一半)
∴AC=BD/2
例2、已知,如图,在△ABC中,D是BC边上一点,DE ⊥AB于点E,DF ⊥AC于点F,且DE=DF,EF与AD交于点O.求证;AD ⊥EF.
A
E O F
B C
D
例3:如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。
说明两条线段相等,有时还可以通过第三条线段进行等量代换。
变式题:如图,已知AD、BE分别是△ABC的BC、AC边上的高,F是DE的中点,G是AB的中点,则FG⊥DE,请说明理由。
F
E
D
C
B
A
例4:如图:AD是△ABC中BC边上的高,E为AC上一点,BE交AD于F,BF=AC,FD=CD,问BE,AC互相垂直么?请说明理由
例4、如图,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,且AP=PC,AP⊥PC,则△ABP≌△PDC,请说明理由。
