沪教版(上海)初中数学七年级第一学期 第10 章 分式 小结 复习课 课件(共24张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 第10 章 分式 小结 复习课 课件(共24张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览






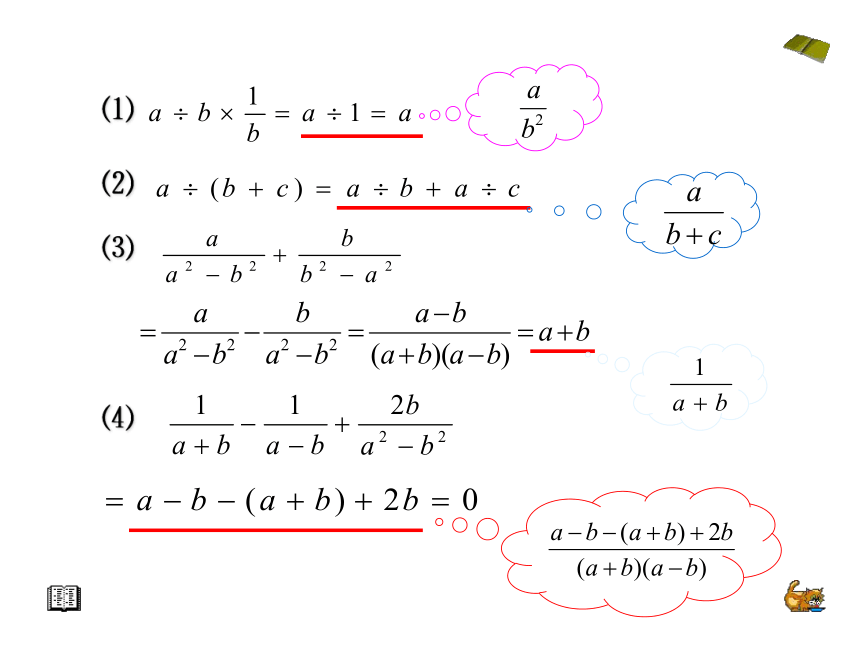


文档简介
1、当取什么值时,分式
(1)没有意义?(2)有意义?
(3)值为零。
2、当x为何值时分式 的值为0?
3、已知分式 当x≠______时,分式有意义;当x=______时,分式的值为0.
你会解决下面这些问题吗?
4、若将分式 (a、b均为正数)中的字母a、b的值分别扩大为原来的2倍,则分式的值为( )
A.扩大为原来的2倍 B.缩小为原来的
C.不变 D.缩小为原来的
5、下列各式中,;
整式有 ,分式 .
6、 下列分式中,最简分式是 ( )
B
7、分式
8、分式
的最简公分母是
的最简公分母是
12a2b
9、下列各式的运算对不对?如果不对,错在哪里?
应怎样改正?
⑴
⑵
⑶
⑷
= 0
⑴
⑵
⑶
⑷
10、把分式方程 的两边同时乘以(x-2), 约去分母,得 ( )
A.1-(1-x)=1 B.1+(1-x)=1
C.1-(1-x)=x-2 D.1+(1-x)=x-2
D
分
式
分式概念
分式方程
分式基本性质
分式乘除法法则
分式加减法法则
分式方程的解法
分式方程的应用
知识结构图
1.下列各代数式中,哪些是分式?
技能训练
2.下列各式中不正确的变形是( )
(A) = (B) =
(C) = (D) =
3.化简 ,并说明化简的根据是什么?
4.求x=2时,分式 的值是多少?
5.使分式 有意义的条件是什么?
使分式 的值为零的条件是什么?
6.计算:
(2) ;
(3) ;
(4) .
(1) ;
7、 先化简,再求值 中
8、解方程:
9、 甲、乙两地相距80公里,一辆卡车从甲地驶 出3小时后 ,一辆轿车也从甲地出发,已知轿车的速度是卡车的3倍,而轿车只比卡车迟20分钟到达乙地,求两车的速度。
课堂小结
(1)建立本章知识体系.
(2)学习了分式的概念及基本性质,分式的有关运算
(3)提高了运算能力和对分式的进一步理解。
通过本节课复习,谈谈本节课的收获:
1、阅读并指出错误
1)上述计算过程中,从哪一步开始出现了错误?
2)从(2)到(3)是否正确?
3)写出正确解答。
(1)
(2)
(3)
(4)
拓展与思考
有一道题“先化简,再求值: ,其中x=-3 。”
小玲做题时把“x=-3”错抄成了“x=3”,但她的计算结果也是正确的,请你解释这是怎么回事?
若关于x的方程 有增根, 则m的值等于( )
A.-3 B.-2 C.-1 D.3
没有实数解
有实数解
若 =___
已知:
若x+y=4,xy=3,求 的值.
4、如果整数A、B满足等式
,求A与B的值。
解:
解得:
例6、某工程要求限期完成,甲队独做正好按期完成,乙队独做则要误期3天,现甲、乙两队合做2天后,余下的工程由乙队独做,正好按期完成,问该工程限期多少天?
例7、正在修建的西塔(西宁~塔尔寺)高速公路上,有一段工程,若甲、乙两个工程队单独完成,甲工程队比乙工程队少用10天;若甲、乙两队合作,12天可以完成.若没甲单独完成这项工程需要x天.则根据题意,可列方程为_______________-
例8、2004年12月28日,我国第一条城际铁路一合宁铁路(合肥至南京)正式开工建设.建成后,合肥至南京的铁路运行里程将由目前的312 km缩短至154 km,设计时速是现行时速的2.5倍,旅客列车运行时间将因此缩短约3.13小时,求合宁铁路的设计时速.
例9、就要毕业了,几位要好的同学准备中考后结伴到某地游玩,预计共需费用1200元,后来又有2名同学参加进来,但总费用不变,于是每人可少分摊30元,试求原计划结伴游玩的人数.
(阅读理解题)阅读下面的解题过程,然后解题:
题目:已知
求x+y+z的值
解:设
=k,
仿照上述方法解答下列问题:
已知:
(1)没有意义?(2)有意义?
(3)值为零。
2、当x为何值时分式 的值为0?
3、已知分式 当x≠______时,分式有意义;当x=______时,分式的值为0.
你会解决下面这些问题吗?
4、若将分式 (a、b均为正数)中的字母a、b的值分别扩大为原来的2倍,则分式的值为( )
A.扩大为原来的2倍 B.缩小为原来的
C.不变 D.缩小为原来的
5、下列各式中,;
整式有 ,分式 .
6、 下列分式中,最简分式是 ( )
B
7、分式
8、分式
的最简公分母是
的最简公分母是
12a2b
9、下列各式的运算对不对?如果不对,错在哪里?
应怎样改正?
⑴
⑵
⑶
⑷
= 0
⑴
⑵
⑶
⑷
10、把分式方程 的两边同时乘以(x-2), 约去分母,得 ( )
A.1-(1-x)=1 B.1+(1-x)=1
C.1-(1-x)=x-2 D.1+(1-x)=x-2
D
分
式
分式概念
分式方程
分式基本性质
分式乘除法法则
分式加减法法则
分式方程的解法
分式方程的应用
知识结构图
1.下列各代数式中,哪些是分式?
技能训练
2.下列各式中不正确的变形是( )
(A) = (B) =
(C) = (D) =
3.化简 ,并说明化简的根据是什么?
4.求x=2时,分式 的值是多少?
5.使分式 有意义的条件是什么?
使分式 的值为零的条件是什么?
6.计算:
(2) ;
(3) ;
(4) .
(1) ;
7、 先化简,再求值 中
8、解方程:
9、 甲、乙两地相距80公里,一辆卡车从甲地驶 出3小时后 ,一辆轿车也从甲地出发,已知轿车的速度是卡车的3倍,而轿车只比卡车迟20分钟到达乙地,求两车的速度。
课堂小结
(1)建立本章知识体系.
(2)学习了分式的概念及基本性质,分式的有关运算
(3)提高了运算能力和对分式的进一步理解。
通过本节课复习,谈谈本节课的收获:
1、阅读并指出错误
1)上述计算过程中,从哪一步开始出现了错误?
2)从(2)到(3)是否正确?
3)写出正确解答。
(1)
(2)
(3)
(4)
拓展与思考
有一道题“先化简,再求值: ,其中x=-3 。”
小玲做题时把“x=-3”错抄成了“x=3”,但她的计算结果也是正确的,请你解释这是怎么回事?
若关于x的方程 有增根, 则m的值等于( )
A.-3 B.-2 C.-1 D.3
没有实数解
有实数解
若 =___
已知:
若x+y=4,xy=3,求 的值.
4、如果整数A、B满足等式
,求A与B的值。
解:
解得:
例6、某工程要求限期完成,甲队独做正好按期完成,乙队独做则要误期3天,现甲、乙两队合做2天后,余下的工程由乙队独做,正好按期完成,问该工程限期多少天?
例7、正在修建的西塔(西宁~塔尔寺)高速公路上,有一段工程,若甲、乙两个工程队单独完成,甲工程队比乙工程队少用10天;若甲、乙两队合作,12天可以完成.若没甲单独完成这项工程需要x天.则根据题意,可列方程为_______________-
例8、2004年12月28日,我国第一条城际铁路一合宁铁路(合肥至南京)正式开工建设.建成后,合肥至南京的铁路运行里程将由目前的312 km缩短至154 km,设计时速是现行时速的2.5倍,旅客列车运行时间将因此缩短约3.13小时,求合宁铁路的设计时速.
例9、就要毕业了,几位要好的同学准备中考后结伴到某地游玩,预计共需费用1200元,后来又有2名同学参加进来,但总费用不变,于是每人可少分摊30元,试求原计划结伴游玩的人数.
(阅读理解题)阅读下面的解题过程,然后解题:
题目:已知
求x+y+z的值
解:设
=k,
仿照上述方法解答下列问题:
已知:
