沪教版(上海)初中数学七年级第一学期 9.14 公式法(1)用平方差公式因数分解 课件(共27张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.14 公式法(1)用平方差公式因数分解 课件(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 316.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览







文档简介
§9.14 公式法(1)
------用平方差公式因数分解
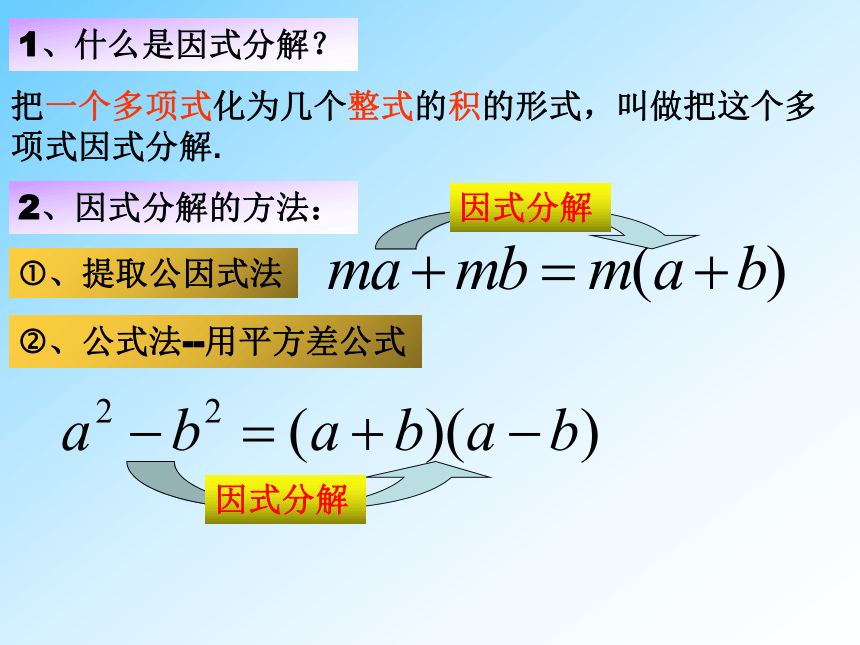
1、什么是因式分解?
2、因式分解的方法:
?、提取公因式法
?、公式法--用平方差公式
把一个多项式化为几个整式的积的形式,叫做把这个多项式因式分解.
因式分解
因式分解
3、因式分解的平方差公式:
能用平方差公式因式分解的多项式须满足:
? 这个多项式两项式;
? 每一项(除了符号)都是平方的形式;
? 两项的系数异号;
课堂练习一
1、分解因式:
(1)
(2)
(3)
1. 把两项写成平方的形式,找出a和b
2. 利用平方差公式分解因式
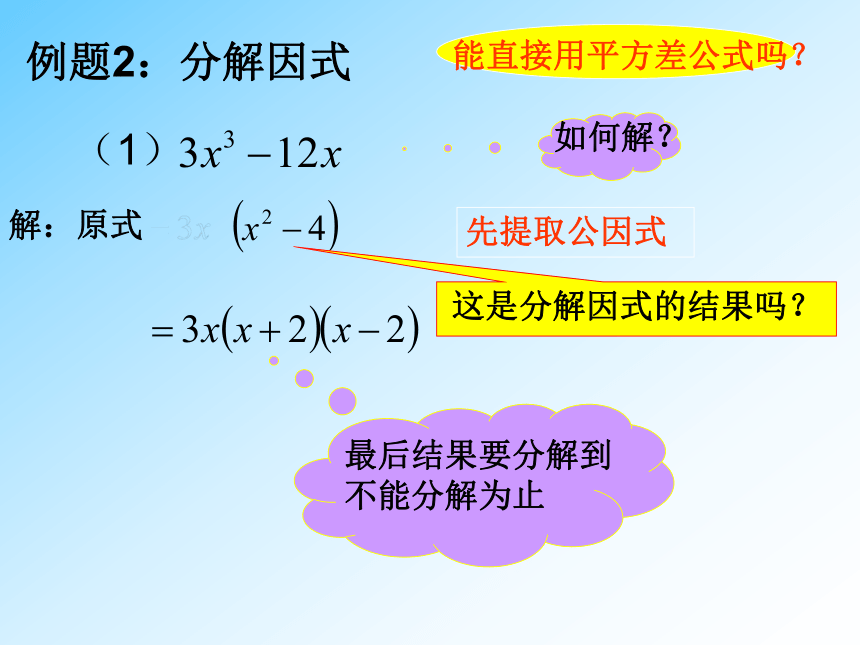
例题2:分解因式
(1)
能直接用平方差公式吗?
如何解?
解:原式
先提取公因式
这是分解因式的结果吗?
最后结果要分解到不能分解为止
(2)
能直接用平方差公式吗?
解:原式
还能继续分解吗?
2、用公式法分解因式;
适时小结:
二项多项式因式分解的一般步骤是:
1、先提取公因式;
3、分解到不能分解为止.
课堂练习二
例题2:用简便方法计算:
解 原式=
四、课堂小结
1、因式分解的平方差公式
2、因式分解的一般步骤:
(1)先提取公因式
(2)用公式法分解因式
(3)分解到不能分解为止
1、什么是“因式分解”?
把一个多项式化为几个整式的积的形式,叫做把这个多项式因式分解.
、
因式分解
整式乘法
一、复习引入
把多项式
因式分解
平方差公式
反过来,可得
逆用乘法公式将一个多项式分解因式的方法叫做公式法.
因式分解的平方差公式.
二、新课探究
试一试
2、因式分解的平方差公式的特征
两个数的
平方差的形式
这两个数的和
与这两个数的差的积.
二项式
思考:哪种多项式可以用平方差公式分解因式?
多项式为二项式,每一项为平方项,并且两个平方项的符号相反.
3、多项式 是否可用平方差公式分解因式?
为什么?
课堂练习一
1、下列多项式能用平方差公式分解因式吗?
快速热身
、
1、填空:
公式:
常取正号
三、例题讲解:
例题1:分解因式
(1)
解:
1. 把两项写成平方的形式,找出a和b
2. 利用
分解因式
例题1:分解因式
(2)
解:
另解:
解:
例题1:分解因式
例题1:分解因式
分别把 看作一个整体,这个多项式也可看作两数的平方差,
解:原式=
-
+
(1)左边应是一个 _______(如: )
(2)两项式的每项(不包含符号)都是一个_____ 形式
(3)两项的符号是 ______。(如: )
运用平方差公式分解因式的特点:
(4)
-
[ ]
[ ]
适时小结
平方
异号
两项式
2、分解因式:
(1)
(2)
(3)
(1)原式=
(2)原式=
(3)原式
解:
解:
解:
课堂练习二
四、课堂小结
1、因式分解的平方差公式
2、平方差公式分解因式的特征:
(1)两项的多项式
(2)这两项分别是平方项
(3)这两项的符号是异号
课堂练习一
1、下列多项式能用平方差公式分解因式吗?
如果可以,请分解因式:
例题2:分解因式
(1)
能直接用平方差公式吗?
如何解?
解:原式
先提取公因式
这是分解因式的结果吗?
最后结果要分解到不能分解为止
(2)
能直接用平方差公式吗?
解:原式
还能继续分解吗?
2、用公式法分解因式;
适时小结:
二项多项式因式分解的一般步骤是:
1、先提取公因式;
3、分解到不能分解为止.
课堂练习二
答案
例题3:用简便方法计算:
解 原式=
四、课堂小结
1、因式分解的平方差公式
2、因式分解的一般步骤:
(1)先提取公因式
(2)用公式法分解因式
(3)分解到不能分解为止
------用平方差公式因数分解
1、什么是因式分解?
2、因式分解的方法:
?、提取公因式法
?、公式法--用平方差公式
把一个多项式化为几个整式的积的形式,叫做把这个多项式因式分解.
因式分解
因式分解
3、因式分解的平方差公式:
能用平方差公式因式分解的多项式须满足:
? 这个多项式两项式;
? 每一项(除了符号)都是平方的形式;
? 两项的系数异号;
课堂练习一
1、分解因式:
(1)
(2)
(3)
1. 把两项写成平方的形式,找出a和b
2. 利用平方差公式分解因式
例题2:分解因式
(1)
能直接用平方差公式吗?
如何解?
解:原式
先提取公因式
这是分解因式的结果吗?
最后结果要分解到不能分解为止
(2)
能直接用平方差公式吗?
解:原式
还能继续分解吗?
2、用公式法分解因式;
适时小结:
二项多项式因式分解的一般步骤是:
1、先提取公因式;
3、分解到不能分解为止.
课堂练习二
例题2:用简便方法计算:
解 原式=
四、课堂小结
1、因式分解的平方差公式
2、因式分解的一般步骤:
(1)先提取公因式
(2)用公式法分解因式
(3)分解到不能分解为止
1、什么是“因式分解”?
把一个多项式化为几个整式的积的形式,叫做把这个多项式因式分解.
、
因式分解
整式乘法
一、复习引入
把多项式
因式分解
平方差公式
反过来,可得
逆用乘法公式将一个多项式分解因式的方法叫做公式法.
因式分解的平方差公式.
二、新课探究
试一试
2、因式分解的平方差公式的特征
两个数的
平方差的形式
这两个数的和
与这两个数的差的积.
二项式
思考:哪种多项式可以用平方差公式分解因式?
多项式为二项式,每一项为平方项,并且两个平方项的符号相反.
3、多项式 是否可用平方差公式分解因式?
为什么?
课堂练习一
1、下列多项式能用平方差公式分解因式吗?
快速热身
、
1、填空:
公式:
常取正号
三、例题讲解:
例题1:分解因式
(1)
解:
1. 把两项写成平方的形式,找出a和b
2. 利用
分解因式
例题1:分解因式
(2)
解:
另解:
解:
例题1:分解因式
例题1:分解因式
分别把 看作一个整体,这个多项式也可看作两数的平方差,
解:原式=
-
+
(1)左边应是一个 _______(如: )
(2)两项式的每项(不包含符号)都是一个_____ 形式
(3)两项的符号是 ______。(如: )
运用平方差公式分解因式的特点:
(4)
-
[ ]
[ ]
适时小结
平方
异号
两项式
2、分解因式:
(1)
(2)
(3)
(1)原式=
(2)原式=
(3)原式
解:
解:
解:
课堂练习二
四、课堂小结
1、因式分解的平方差公式
2、平方差公式分解因式的特征:
(1)两项的多项式
(2)这两项分别是平方项
(3)这两项的符号是异号
课堂练习一
1、下列多项式能用平方差公式分解因式吗?
如果可以,请分解因式:
例题2:分解因式
(1)
能直接用平方差公式吗?
如何解?
解:原式
先提取公因式
这是分解因式的结果吗?
最后结果要分解到不能分解为止
(2)
能直接用平方差公式吗?
解:原式
还能继续分解吗?
2、用公式法分解因式;
适时小结:
二项多项式因式分解的一般步骤是:
1、先提取公因式;
3、分解到不能分解为止.
课堂练习二
答案
例题3:用简便方法计算:
解 原式=
四、课堂小结
1、因式分解的平方差公式
2、因式分解的一般步骤:
(1)先提取公因式
(2)用公式法分解因式
(3)分解到不能分解为止
