沪教版(上海)初中数学七年级第一学期 9.14 因式分解—公式法-完全平方公式 课件(共22张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.14 因式分解—公式法-完全平方公式 课件(共22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 864.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 19:02:56 | ||
图片预览







文档简介
因式分解——公式法(2)
完全平方公式
一、复习引入、温故知新
什么叫因式分解?
把一个多项式化成几个整式乘积形式,叫做把这个多项式因式分解。
我们已经学习了哪些因式分解的方法?
我们学过的因式分解方法有提取公因式法及运用平方差公式法。
复习:把下列各式因式分解:
(1)ax4﹣ax2
原式=ax2(x2-1)
=ax2(x+1)(x-1)
(2)16m4-n4
原式=(4m2)2-(n2)2
=(4m2+n2)(4m2-n2)
=(4m2+n2)(2m+n)(2m-n)
思考:我们学过的乘法公式除了平方差公式以外,还
有哪些公式?
完全平方公式:
(a+b)2 =a2+2ab+b2
(a-b)2 =a2-2ab+b2
二、观察特征、探究新知
和讨论运用平方差公式因式分解的思路一样,把完全平方公式反过来:
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
我们可以用这个公式来因式分解了,把它称为“完全平方公式”
完全平方式
a2+2ab+b2
a2-2ab+b2
观察:具备什么特征的多项式是完全平方式?
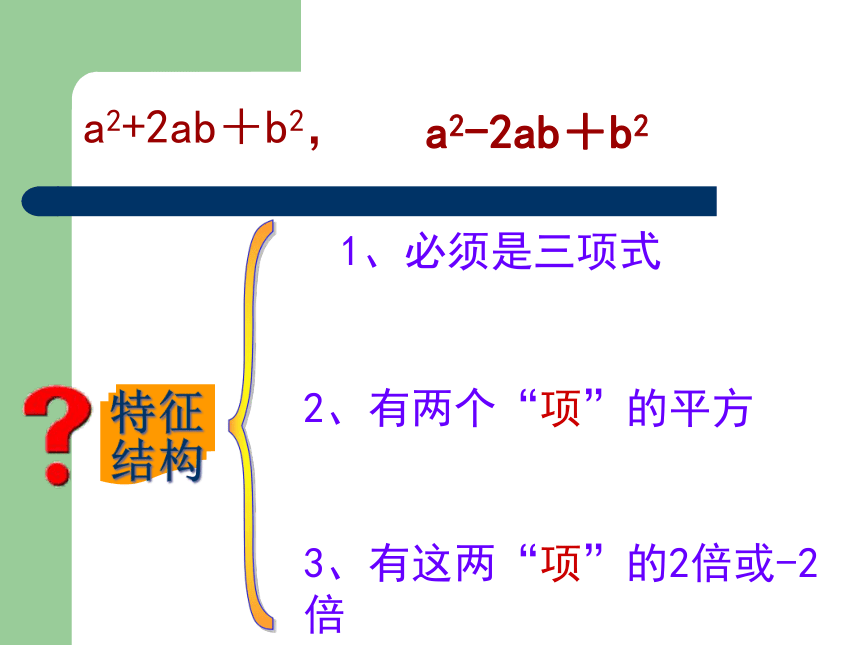
特征
结构
1、必须是三项式
2、有两个“项”的平方
3、有这两“项”的2倍或-2倍
a2-2ab+b2
a2+2ab+b2,
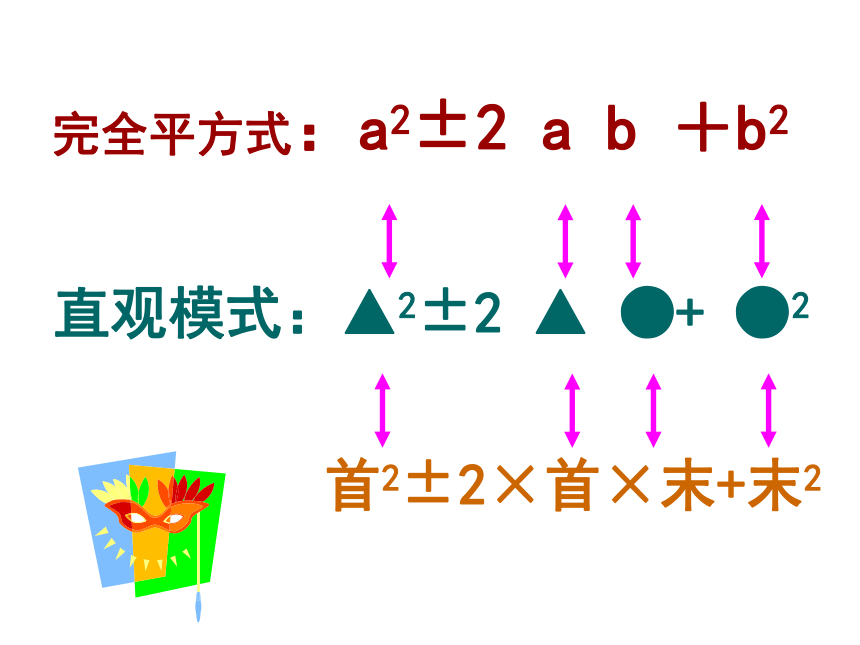
完全平方式:a2±2 a b +b2
直观模式:▲2±2 ▲ ●+ ●2
首2±2×首×末+末2
练习1:判断下列是不是完全平方式,为什么?
(1) x2+xy+y2
(2) x2+6x+9
(3) 16a2+1
(4)-2xy+x2+y2
(5) a2-6ab+b2
(6) 25x4-10x2+1
(7) x2+x+1/4
(8) 1-m+m2/4
否
否
否
是
是
是
是
是
练习2:请补上一项,使下列多项式成为完全平方式
请每一组同学们根据完全平方式的特点写出一个完全平方式
练习3:
a2±2ab+b2=(a±b)2
我们可以通过以上公式把“完全平方式”分解因式
我们称之为:运用完全平方公式分解因式
三、启发诱导,初步运用
例题1:把下列各式因式分解
(1)9x2+12x+4 (2)4x2-20xy+25y2
解:(1)原式=(3x)2+2·(3x)·2+22=(3x+2)2
a 2 + 2 · a · b+b 2 =( a + b)2
(2)原式=(2x)2 -2 (2x)(5y)+(5y)2=(2x-5y)2
a 2 - 2 · a · b + b 2 = ( a - b)2
(
(3) (4)
解:(3)原式=
=
(4)原式=
=
此题将(1/2a)看作a,(3/5b)看作b
注意应先提取负号
四、尝试练习,反馈矫正
课堂练习1:分解因式
(1)m2+m+1/4 (2)x2-16xy+64y2
(3)9x+1/4+81x2 (4)-m2n2-16+8mn
五、拓展练习、深化提高
例题2:因式分解
(1)2a2-12axy+18ay2 (2)(x+y)2+8(x+y)+16
解(1)原式=2a(x2-6xy+9y2)
=2a(x-3y)2
(2) 原式=( x+y )2+2·( x+y )· 4 + 4 2
=( x+y + 4 )2
因式分解时,应先提取公因式,然后再用公式法分解因式。
把(x+y)看作a,把4看作b。
换元
思想
五、拓展练习、深化提高
课堂练习2:分解因式
(1)-6x2y-3x3-3xy2
(2)(2x-y)2-10(2x-y)+25
比一比、赛一赛
请每一组同学编一道因式分解题。
要求:
(1)必须用到完全平方公式
(2)必须用换元思想
思考题:
1、计算 1002-2×100×99+992 的结果是_______
2、如果x2+mxy+9y2是一个完全平方式,那么m的 值为________
3、在括号内补上一项,使多项式成为完全平方式:X4+4x2+______
六、学后感想、畅所欲言
本节课你学会了什么?
1.完全平方式 a2±2ab+b2
2.用完全平方公式因式分解
a2±2ab+b2=(a±b)2
用公式法分解因式要注意些什么?
1、基础训练:教材P48 练习8.14(2)。
2、拓展训练:
多项式:(x+y)2-2(x2-y2)+(x-y)2
能用完全平方公式分解吗?
七、分层作业
请各位老师指正
完全平方公式
一、复习引入、温故知新
什么叫因式分解?
把一个多项式化成几个整式乘积形式,叫做把这个多项式因式分解。
我们已经学习了哪些因式分解的方法?
我们学过的因式分解方法有提取公因式法及运用平方差公式法。
复习:把下列各式因式分解:
(1)ax4﹣ax2
原式=ax2(x2-1)
=ax2(x+1)(x-1)
(2)16m4-n4
原式=(4m2)2-(n2)2
=(4m2+n2)(4m2-n2)
=(4m2+n2)(2m+n)(2m-n)
思考:我们学过的乘法公式除了平方差公式以外,还
有哪些公式?
完全平方公式:
(a+b)2 =a2+2ab+b2
(a-b)2 =a2-2ab+b2
二、观察特征、探究新知
和讨论运用平方差公式因式分解的思路一样,把完全平方公式反过来:
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
我们可以用这个公式来因式分解了,把它称为“完全平方公式”
完全平方式
a2+2ab+b2
a2-2ab+b2
观察:具备什么特征的多项式是完全平方式?
特征
结构
1、必须是三项式
2、有两个“项”的平方
3、有这两“项”的2倍或-2倍
a2-2ab+b2
a2+2ab+b2,
完全平方式:a2±2 a b +b2
直观模式:▲2±2 ▲ ●+ ●2
首2±2×首×末+末2
练习1:判断下列是不是完全平方式,为什么?
(1) x2+xy+y2
(2) x2+6x+9
(3) 16a2+1
(4)-2xy+x2+y2
(5) a2-6ab+b2
(6) 25x4-10x2+1
(7) x2+x+1/4
(8) 1-m+m2/4
否
否
否
是
是
是
是
是
练习2:请补上一项,使下列多项式成为完全平方式
请每一组同学们根据完全平方式的特点写出一个完全平方式
练习3:
a2±2ab+b2=(a±b)2
我们可以通过以上公式把“完全平方式”分解因式
我们称之为:运用完全平方公式分解因式
三、启发诱导,初步运用
例题1:把下列各式因式分解
(1)9x2+12x+4 (2)4x2-20xy+25y2
解:(1)原式=(3x)2+2·(3x)·2+22=(3x+2)2
a 2 + 2 · a · b+b 2 =( a + b)2
(2)原式=(2x)2 -2 (2x)(5y)+(5y)2=(2x-5y)2
a 2 - 2 · a · b + b 2 = ( a - b)2
(
(3) (4)
解:(3)原式=
=
(4)原式=
=
此题将(1/2a)看作a,(3/5b)看作b
注意应先提取负号
四、尝试练习,反馈矫正
课堂练习1:分解因式
(1)m2+m+1/4 (2)x2-16xy+64y2
(3)9x+1/4+81x2 (4)-m2n2-16+8mn
五、拓展练习、深化提高
例题2:因式分解
(1)2a2-12axy+18ay2 (2)(x+y)2+8(x+y)+16
解(1)原式=2a(x2-6xy+9y2)
=2a(x-3y)2
(2) 原式=( x+y )2+2·( x+y )· 4 + 4 2
=( x+y + 4 )2
因式分解时,应先提取公因式,然后再用公式法分解因式。
把(x+y)看作a,把4看作b。
换元
思想
五、拓展练习、深化提高
课堂练习2:分解因式
(1)-6x2y-3x3-3xy2
(2)(2x-y)2-10(2x-y)+25
比一比、赛一赛
请每一组同学编一道因式分解题。
要求:
(1)必须用到完全平方公式
(2)必须用换元思想
思考题:
1、计算 1002-2×100×99+992 的结果是_______
2、如果x2+mxy+9y2是一个完全平方式,那么m的 值为________
3、在括号内补上一项,使多项式成为完全平方式:X4+4x2+______
六、学后感想、畅所欲言
本节课你学会了什么?
1.完全平方式 a2±2ab+b2
2.用完全平方公式因式分解
a2±2ab+b2=(a±b)2
用公式法分解因式要注意些什么?
1、基础训练:教材P48 练习8.14(2)。
2、拓展训练:
多项式:(x+y)2-2(x2-y2)+(x-y)2
能用完全平方公式分解吗?
七、分层作业
请各位老师指正
