沪教版(上海)初中数学七年级第一学期 9.16 分组分解法 课件(共21张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.16 分组分解法 课件(共21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 363.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 19:01:56 | ||
图片预览




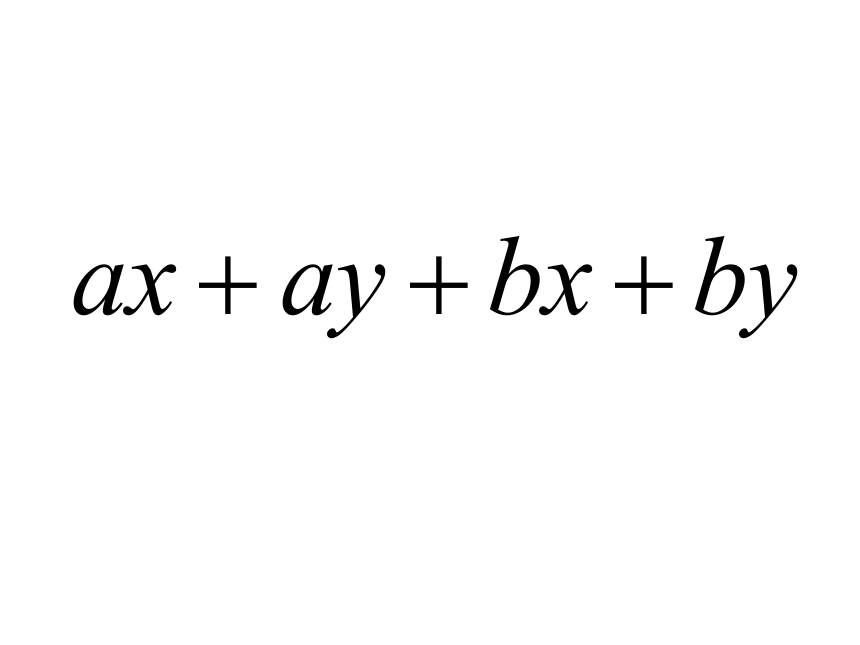

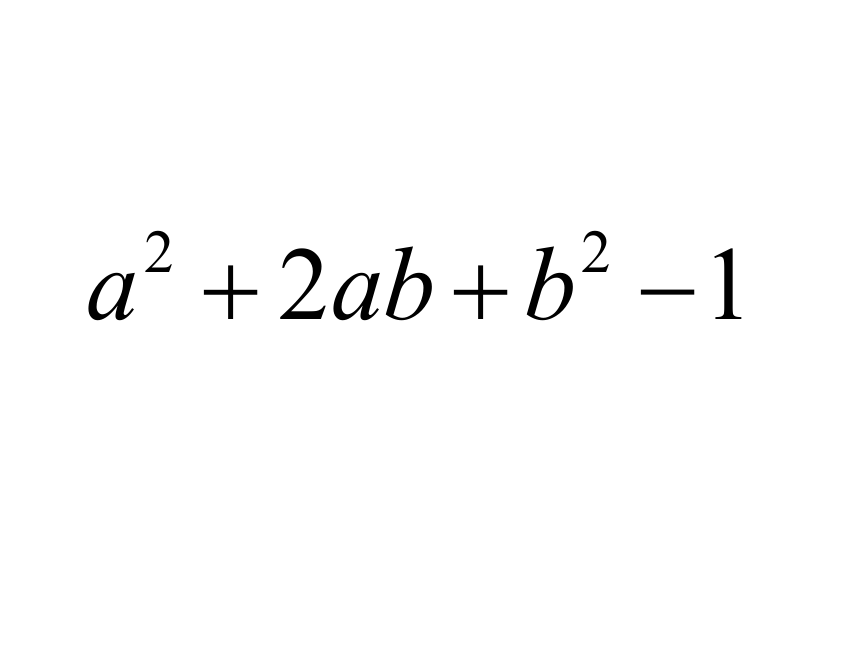
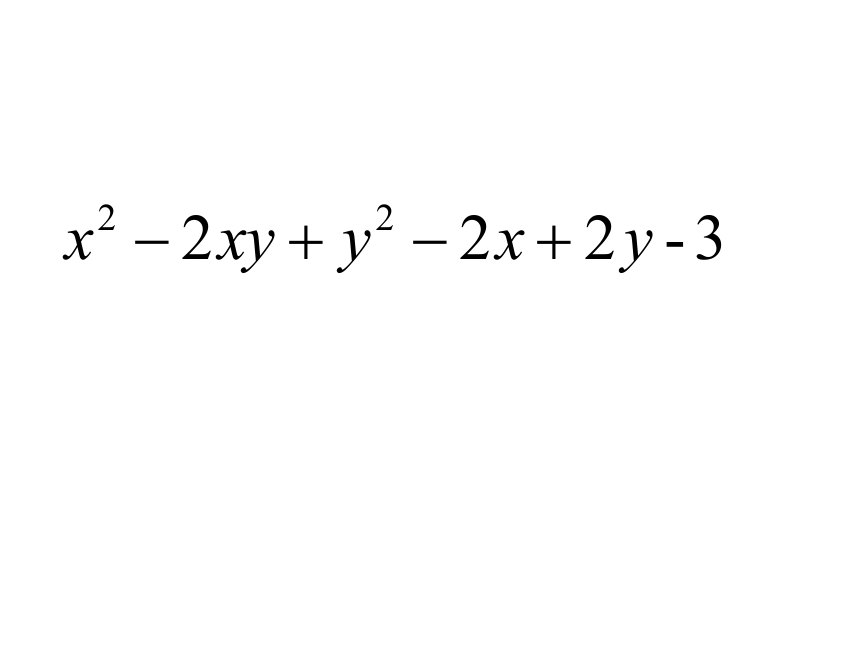

文档简介
§分组分解法
复习
1,请大家回忆一下前面所学的分解因式的方法;
2,各种分解方法所适用的多项式具有怎样的特征?
口答:下列多项式用什么方法分解?
思考
如何将多项式
和 分解因式?
观察上面两式的特征?
定义:
利用分组来分解因式的方法叫做分组分解法。
定义:
1.理解分组分解法在因式分解中的重要意义.
2.在运用分组分解法分解因式时,会筛选合理
的分组方案.
3.能综合运用各种方法完成因式分解.
一、学习目标
本节的重点:运用分组分解法分解因式.
本节的难点:筛选合理的分组方案和综合
运用各种方法完成因式分解.
二、重点难点
很多多项式(四项)不能直接运用提公因式法或直接运用公式法分解,但是,进行分组后,就可以先在局部上,进而在整体上运用这两种方法进行分解,使问题迎刃而解.所以,“分组”的作用在于促进了提公因式法和公式法的运用,使多项式从不能分解向能分解转化.
三、引入
练习
分解因式:
【解法一】a3-a2b-ab2+b3
=(a3-a2b)-(ab2-b3)
=a2(a-b)-b2(a-b)
=(a-b)(a2-b2)
=(a-b)2(a+b)
【解法二】a3-a2b-ab2+b3
=(a3-ab2)-(a2b-b3)
=a(a2-b2)-b(a2-b2)
=(a2-b2)(a-b)
=(a-b)2(a+b)
a3-a2b-ab2+b3
注意,分解的
结果中,如果有相
同的因式,要写成
乘方的形式.本题
的结果不要写成
(a-b)(a-b)(a+b).
分解因式:
【注意】
(4)实际上,分组只是为完成分解创造条件,并没有直接达到分解的目的.
(1)分组要合理:把有公因式的各项归为一组,并使组之间产生新的公因式,这是正确分组的关键,因此,设计分组方案是否有效要有预见性.
(2)分组的方法不唯一;
(3)整体思想的应用
(4)分组时要用到添括号法则,注意在添加带有“-”号的括号时,括号内每项的符号都要改变.
(5)有相同因式写成乘方的形式
(6)检查是否分解完全
方法
分类
分组方法
特点
分组分解法
四项
二项、二项
①按字母分组②按系数分组③符合公式的两项分组
三项、一项
先完全平方公式后平方差公式
五项
三项、二项
各组之间有公因式
六项
三项、三项
二项、二项、二项
各组之间有公因式
三项、二项、一项
可化为二次三项式
练 习
把下列各式分解因式:
10.(z2-x2-y2)2-4x2y2
提高练习:
把下列各式分解因式:
4. 课堂小结
(1)运用分组分解法分解因式的关键是合理
分组,要预见分组后组与组之间还能否
继续进行因式分解。分组时可进行尝试,
最后找到合理的分组方法。
局部入手, 兼顾全局,
自觉试验,合理分组.
4. 课堂小结
(2)分组分解法也是恒等变形的一种手段,
它有着广泛的应用,如引例中通过分组分解法做恒等变形后简化了计算。
4. 课堂小结
(3)利用分组的手段为提公因式法创造条件,
因此分组分解法是转化的数学思想在因式
分解中的集中体现,分组的目的是经过适
当的分组以后,将原来不显现的条件通过
分组显现出来,将其转化为用已学过的提
公因式法或运用公式法来进行因式分解。
通过分组分解法的学习,我们可以体会到
数学思想方法对数学学习的重要意义。
小 结
常见题型有:
3.运用公式
分解首项系数是1的二次三项式.
1.分组后可以直接提公因式.
2.分组后能利用公式.
(1)能利用平方差公式
(2)能利用完全平方公式
复习
1,请大家回忆一下前面所学的分解因式的方法;
2,各种分解方法所适用的多项式具有怎样的特征?
口答:下列多项式用什么方法分解?
思考
如何将多项式
和 分解因式?
观察上面两式的特征?
定义:
利用分组来分解因式的方法叫做分组分解法。
定义:
1.理解分组分解法在因式分解中的重要意义.
2.在运用分组分解法分解因式时,会筛选合理
的分组方案.
3.能综合运用各种方法完成因式分解.
一、学习目标
本节的重点:运用分组分解法分解因式.
本节的难点:筛选合理的分组方案和综合
运用各种方法完成因式分解.
二、重点难点
很多多项式(四项)不能直接运用提公因式法或直接运用公式法分解,但是,进行分组后,就可以先在局部上,进而在整体上运用这两种方法进行分解,使问题迎刃而解.所以,“分组”的作用在于促进了提公因式法和公式法的运用,使多项式从不能分解向能分解转化.
三、引入
练习
分解因式:
【解法一】a3-a2b-ab2+b3
=(a3-a2b)-(ab2-b3)
=a2(a-b)-b2(a-b)
=(a-b)(a2-b2)
=(a-b)2(a+b)
【解法二】a3-a2b-ab2+b3
=(a3-ab2)-(a2b-b3)
=a(a2-b2)-b(a2-b2)
=(a2-b2)(a-b)
=(a-b)2(a+b)
a3-a2b-ab2+b3
注意,分解的
结果中,如果有相
同的因式,要写成
乘方的形式.本题
的结果不要写成
(a-b)(a-b)(a+b).
分解因式:
【注意】
(4)实际上,分组只是为完成分解创造条件,并没有直接达到分解的目的.
(1)分组要合理:把有公因式的各项归为一组,并使组之间产生新的公因式,这是正确分组的关键,因此,设计分组方案是否有效要有预见性.
(2)分组的方法不唯一;
(3)整体思想的应用
(4)分组时要用到添括号法则,注意在添加带有“-”号的括号时,括号内每项的符号都要改变.
(5)有相同因式写成乘方的形式
(6)检查是否分解完全
方法
分类
分组方法
特点
分组分解法
四项
二项、二项
①按字母分组②按系数分组③符合公式的两项分组
三项、一项
先完全平方公式后平方差公式
五项
三项、二项
各组之间有公因式
六项
三项、三项
二项、二项、二项
各组之间有公因式
三项、二项、一项
可化为二次三项式
练 习
把下列各式分解因式:
10.(z2-x2-y2)2-4x2y2
提高练习:
把下列各式分解因式:
4. 课堂小结
(1)运用分组分解法分解因式的关键是合理
分组,要预见分组后组与组之间还能否
继续进行因式分解。分组时可进行尝试,
最后找到合理的分组方法。
局部入手, 兼顾全局,
自觉试验,合理分组.
4. 课堂小结
(2)分组分解法也是恒等变形的一种手段,
它有着广泛的应用,如引例中通过分组分解法做恒等变形后简化了计算。
4. 课堂小结
(3)利用分组的手段为提公因式法创造条件,
因此分组分解法是转化的数学思想在因式
分解中的集中体现,分组的目的是经过适
当的分组以后,将原来不显现的条件通过
分组显现出来,将其转化为用已学过的提
公因式法或运用公式法来进行因式分解。
通过分组分解法的学习,我们可以体会到
数学思想方法对数学学习的重要意义。
小 结
常见题型有:
3.运用公式
分解首项系数是1的二次三项式.
1.分组后可以直接提公因式.
2.分组后能利用公式.
(1)能利用平方差公式
(2)能利用完全平方公式
