沪教版(上海)数学九年级第二学期-27.4 直线与圆的位置关系 课件 (1)(共18张ppt)
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-27.4 直线与圆的位置关系 课件 (1)(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 235.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览


文档简介
27.4直线与圆的位置关系
一、复习引入
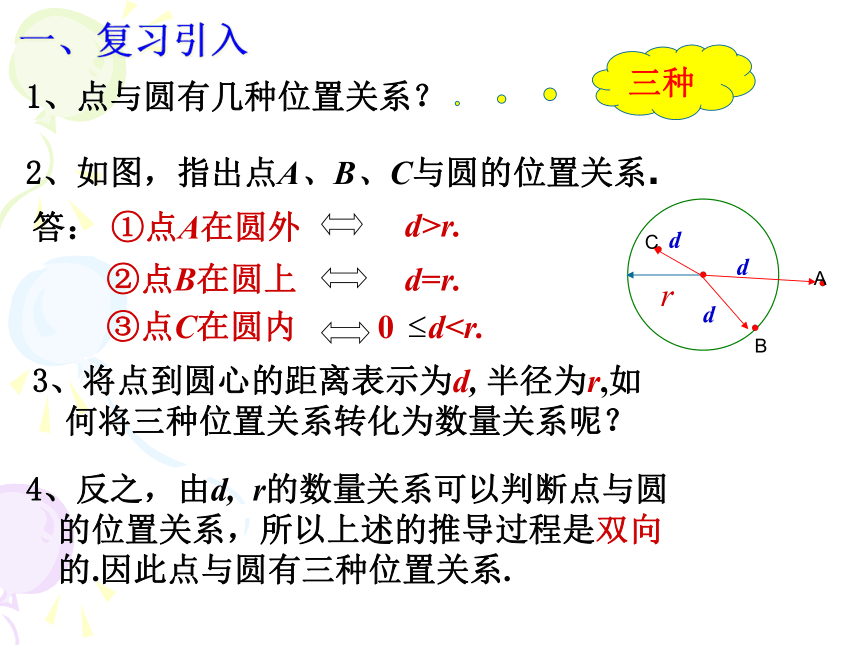
1、点与圆有几种位置关系?
答: ①点A在圆外
②点B在圆上
③点C在圆内
2、如图,指出点A、B、C与圆的位置关系.
d>r.
d=r.
0 d3、将点到圆心的距离表示为d, 半径为r,如 何将三种位置关系转化为数量关系呢?
r
4、反之,由d, r的数量关系可以判断点与圆的位置关系,所以上述的推导过程是双向的.因此点与圆有三种位置关系.
三种
d
d
d
二、探究新知
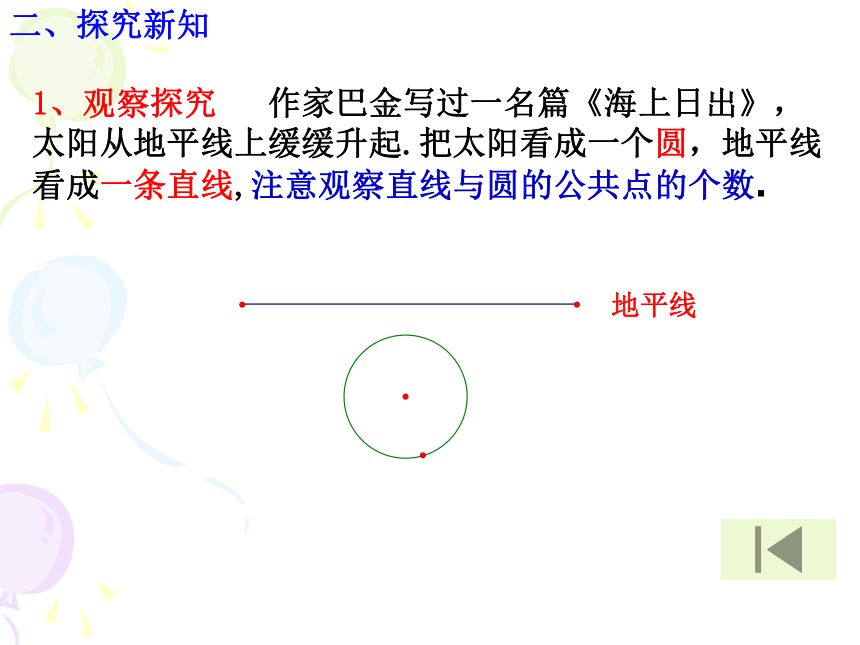
1、观察探究 作家巴金写过一名篇《海上日出》,太阳从地平线上缓缓升起.把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数.
地平线
问1:你发现这个自然现象反映出直线和圆的公共点个数有几种情况?
答:三种.
问2:说说直线与圆的位置关系有几种?
三种
2、归纳小结:
(1)当直线与圆没有公共点时,称为直线与圆相离.
(2)当直线与圆只有一个公共点时,称为直线与圆相
切,此时这条直线叫做圆的切线,这个公共点叫切点.
(3)当直线与圆有两个公共点时,称为直线与圆相交.
此时这条直线叫做圆的割线.
二、探究新知
没有公共点,
一个公共点,
两个公共点.
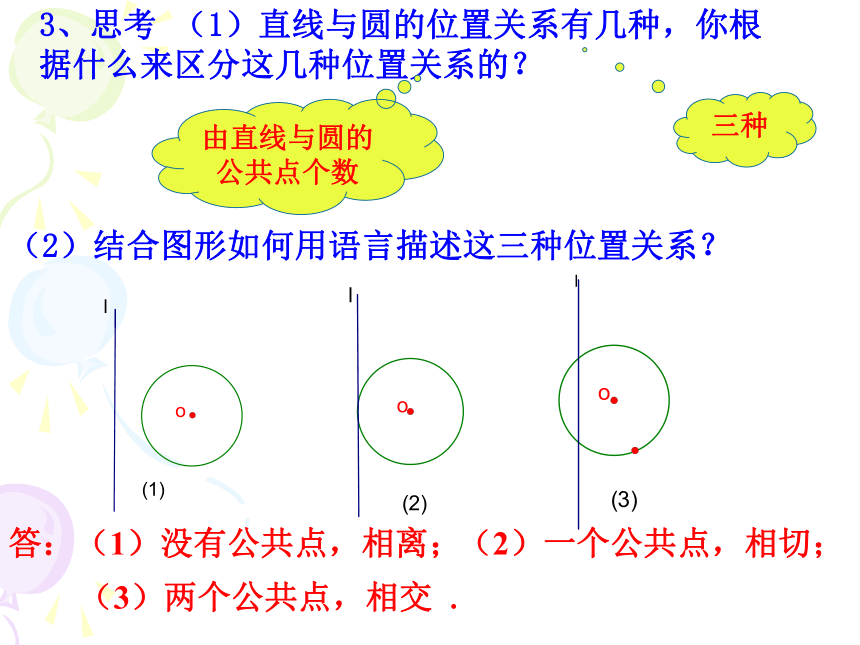
3、思考 (1)直线与圆的位置关系有几种,你根据什么来区分这几种位置关系的?
三种
(2)结合图形如何用语言描述这三种位置关系?
答:(1)没有公共点,相离;
(2)一个公共点,相切;
(3)两个公共点,相交 .
由直线与圆的公共点个数
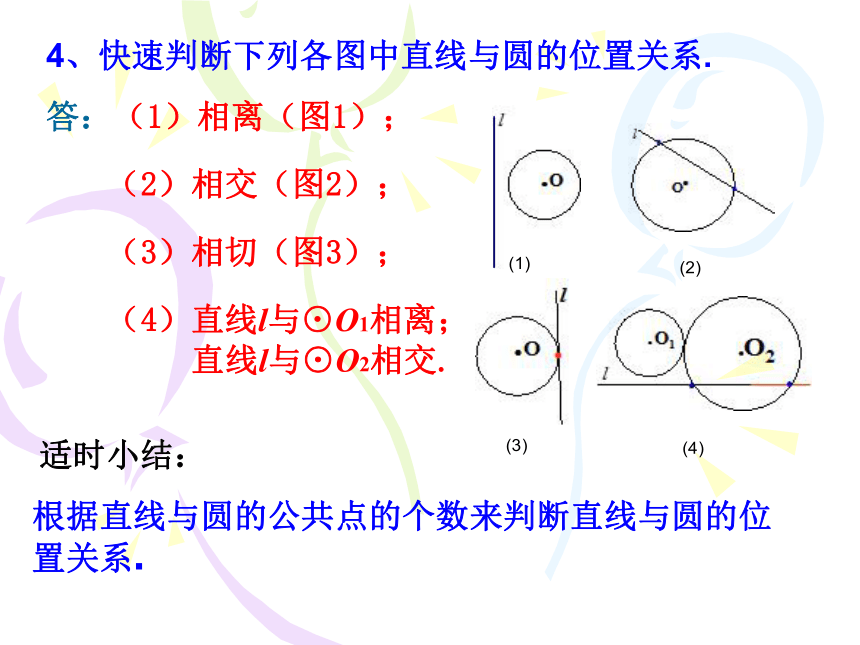
4、快速判断下列各图中直线与圆的位置关系.
答:(1)相离(图1);
(2)相交(图2);
(3)相切(图3);
(4)直线l与⊙O1相离;
直线l与⊙O2相交.
适时小结:
根据直线与圆的公共点的个数来判断直线与圆的位置关系.
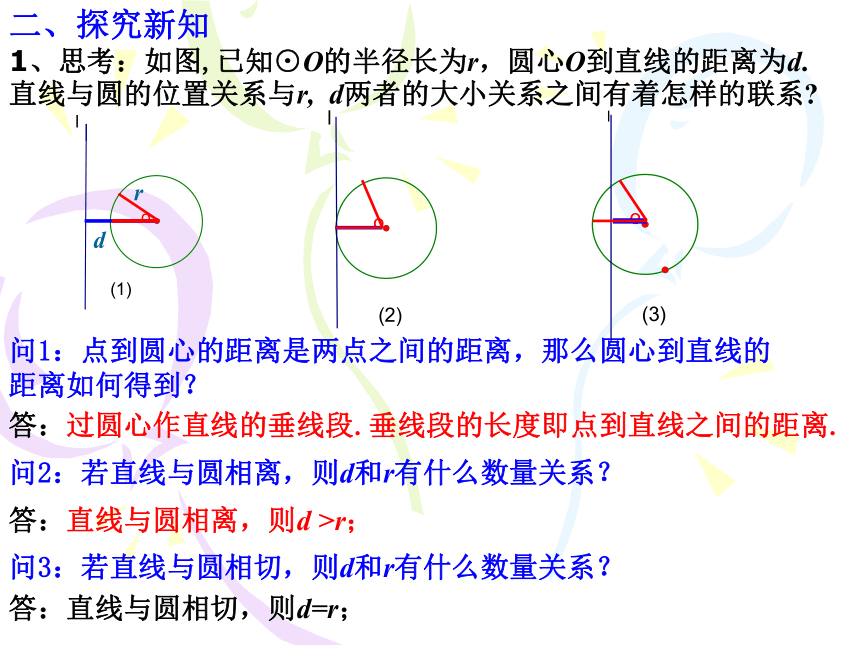
1、思考:如图,已知⊙O的半径长为r,圆心O到直线的距离为d.直线与圆的位置关系与r, d两者的大小关系之间有着怎样的联系?
二、探究新知
问1:点到圆心的距离是两点之间的距离,那么圆心到直线的 距离如何得到?
问2:若直线与圆相离,则d和r有什么数量关系?
答:过圆心作直线的垂线段.垂线段的长度即点到直线之间的距离.
d
r
答:直线与圆相离,则d >r;
问3:若直线与圆相切,则d和r有什么数量关系?
答:直线与圆相切,则d=r;
1、思考:如图,已知⊙O的半径长为r,圆心O到直线的距离为d.直线与圆的位置关系与r,d两者的大小关系之间有着怎样的联系?
二、探究新知
问2:若直线与圆相离,则d和r有什么数量关系?
d
r
答:直线与圆相离,则d >r;
答:直线与圆相交,则0 d < r;
问3:若直线与圆相切,则d 和r 有什么数量关系?
答:直线与圆相切,则d=r;
问4:若直线与圆相交,则d和r有什么数量关系?
问5:d=0时,直线有什么特点?
答:直线过圆心与圆相交.
问6:你能根据d与r的大小关系确定直线与圆的位置关系吗?
答:d > r 直线与圆相离
d=r 直线与圆相切
0 d < r 直线与圆相交
小结:可见它们也是可逆的.从左到右可以得到直线与圆不同位置时的性质,从右到左可以判定直线与圆的不同位置关系.
这条直线叫切线
由此可得:切线判定定理
二、探究新知
经过半径的外端且垂直于这条半径的直线是圆的切线.
证明: 直线 l OA,垂足为点A,
已知:OA是⊙O的半径,直线l与OA垂直,垂足是点A.
求证:直线l是⊙O的切线.
半径OA表示点O 到直线l的距离.
圆心O到 l 的距离等于半径长,
直线l是⊙O的切线.
三、新知运用
请学生在书本P21作图
1、经过⊙O上一点M作⊙O的切线.
分析:1)作半径,即联结OM;
2)过M作直线 l OM.
2、口答 :
1)①直线和圆有2个公共点,则直线和圆 _________;
②直线和圆只有1个公共点,则直线和圆_________;
③直线和圆没有公共点,则直线和圆 _________.
相交
相切
相离
2)已知⊙O的半径为6cm,圆心O与直线AB的距离为d, 根据条件填写d的范围:
①若AB和⊙O相离,则 ;
②若AB和⊙O相切,则 ;
③若AB和⊙O相交,则 .
三、新知运用
例题1、在RtΔABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1) r=2cm; (2) r=2.4cm ; (3) r=3cm.
分析:
已知⊙C的半径
求圆心C到直线AB的距离
关键
RtΔABC斜边AB边上的高
转化
过点C向AB作垂线段CD
根据CD(d)的长度与r进行比较,确定⊙C与AB的关系.
D
三、新知运用
例题1、在RtΔABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1) r=2cm; (2) r=2.4cm; (3) r=3cm.
D
解:过C作CD⊥AB,垂足为D,在RtΔABC中,
根据三角形的面积公式有
CD=
即圆心C到AB的距离d=2.4cm
①当r=2cm时,由d> r,因此⊙C和AB相离.
②当r=2.4cm时,由d= r,因此⊙C和AB相切.
③当r=3cm时,由d< r,因此⊙C和AB相交.
1:在上题中,若以点C为圆心的圆与斜边AB没有公共点,则⊙C的半径的取值范围是什么?
D
答:没公共点
将“没有公共点”,改成“两个公共点”呢?
2:在上题中,若⊙C与边AB只有一个公共点,则圆半径r应取怎样的值?
答: .
或
或 .
两个公共点
变式
已知:如图所示,∠AOB= ,M为OB上一点,以M为圆
心, 5cm长为半径作圆,若M在OB上运动,问:
① 当OM满足 时,⊙M与OA相离.
四、拓展提高
② 当OM满足 时,⊙M与OA相切.
③ 当OM满足 时,⊙M与OA相交.
本节课学习了哪些知识 ?
直线与圆的位置关系
公共点个数
圆心到直线距离d与半径r的关系
公共点的名称
直线名称
1、填表形成结构
五、自主小结
2
1
0
d = r
d > r
割线
交点
切点
无
切线
无
相交
相切
相离
五、自主小结
2、判定直线与圆的位置关系的方法有两种:
(1)根据定义,由直线与圆的公共点的个数来判断;
(2)根据性质,由圆心到直线的距离d与半径r的关系
来判断.
3、切线的判定定理.
经过半径的外端且垂直于这条半径的直线是圆的切线.
六、回家作业
1、阅读课本P19~21.
2、练习册:27.4
3、选做:已知点P到直线的距离为3,以点P为圆心、r为半径画圆,
(1)如果圆上有且只有一个点到直线的距离为2,求半径r 的值.
(2)如果圆上有且只有两个点到直线的距离均为2,求半径r 的取值范围.
一、复习引入
1、点与圆有几种位置关系?
答: ①点A在圆外
②点B在圆上
③点C在圆内
2、如图,指出点A、B、C与圆的位置关系.
d>r.
d=r.
0 d
r
4、反之,由d, r的数量关系可以判断点与圆的位置关系,所以上述的推导过程是双向的.因此点与圆有三种位置关系.
三种
d
d
d
二、探究新知
1、观察探究 作家巴金写过一名篇《海上日出》,太阳从地平线上缓缓升起.把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数.
地平线
问1:你发现这个自然现象反映出直线和圆的公共点个数有几种情况?
答:三种.
问2:说说直线与圆的位置关系有几种?
三种
2、归纳小结:
(1)当直线与圆没有公共点时,称为直线与圆相离.
(2)当直线与圆只有一个公共点时,称为直线与圆相
切,此时这条直线叫做圆的切线,这个公共点叫切点.
(3)当直线与圆有两个公共点时,称为直线与圆相交.
此时这条直线叫做圆的割线.
二、探究新知
没有公共点,
一个公共点,
两个公共点.
3、思考 (1)直线与圆的位置关系有几种,你根据什么来区分这几种位置关系的?
三种
(2)结合图形如何用语言描述这三种位置关系?
答:(1)没有公共点,相离;
(2)一个公共点,相切;
(3)两个公共点,相交 .
由直线与圆的公共点个数
4、快速判断下列各图中直线与圆的位置关系.
答:(1)相离(图1);
(2)相交(图2);
(3)相切(图3);
(4)直线l与⊙O1相离;
直线l与⊙O2相交.
适时小结:
根据直线与圆的公共点的个数来判断直线与圆的位置关系.
1、思考:如图,已知⊙O的半径长为r,圆心O到直线的距离为d.直线与圆的位置关系与r, d两者的大小关系之间有着怎样的联系?
二、探究新知
问1:点到圆心的距离是两点之间的距离,那么圆心到直线的 距离如何得到?
问2:若直线与圆相离,则d和r有什么数量关系?
答:过圆心作直线的垂线段.垂线段的长度即点到直线之间的距离.
d
r
答:直线与圆相离,则d >r;
问3:若直线与圆相切,则d和r有什么数量关系?
答:直线与圆相切,则d=r;
1、思考:如图,已知⊙O的半径长为r,圆心O到直线的距离为d.直线与圆的位置关系与r,d两者的大小关系之间有着怎样的联系?
二、探究新知
问2:若直线与圆相离,则d和r有什么数量关系?
d
r
答:直线与圆相离,则d >r;
答:直线与圆相交,则0 d < r;
问3:若直线与圆相切,则d 和r 有什么数量关系?
答:直线与圆相切,则d=r;
问4:若直线与圆相交,则d和r有什么数量关系?
问5:d=0时,直线有什么特点?
答:直线过圆心与圆相交.
问6:你能根据d与r的大小关系确定直线与圆的位置关系吗?
答:d > r 直线与圆相离
d=r 直线与圆相切
0 d < r 直线与圆相交
小结:可见它们也是可逆的.从左到右可以得到直线与圆不同位置时的性质,从右到左可以判定直线与圆的不同位置关系.
这条直线叫切线
由此可得:切线判定定理
二、探究新知
经过半径的外端且垂直于这条半径的直线是圆的切线.
证明: 直线 l OA,垂足为点A,
已知:OA是⊙O的半径,直线l与OA垂直,垂足是点A.
求证:直线l是⊙O的切线.
半径OA表示点O 到直线l的距离.
圆心O到 l 的距离等于半径长,
直线l是⊙O的切线.
三、新知运用
请学生在书本P21作图
1、经过⊙O上一点M作⊙O的切线.
分析:1)作半径,即联结OM;
2)过M作直线 l OM.
2、口答 :
1)①直线和圆有2个公共点,则直线和圆 _________;
②直线和圆只有1个公共点,则直线和圆_________;
③直线和圆没有公共点,则直线和圆 _________.
相交
相切
相离
2)已知⊙O的半径为6cm,圆心O与直线AB的距离为d, 根据条件填写d的范围:
①若AB和⊙O相离,则 ;
②若AB和⊙O相切,则 ;
③若AB和⊙O相交,则 .
三、新知运用
例题1、在RtΔABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1) r=2cm; (2) r=2.4cm ; (3) r=3cm.
分析:
已知⊙C的半径
求圆心C到直线AB的距离
关键
RtΔABC斜边AB边上的高
转化
过点C向AB作垂线段CD
根据CD(d)的长度与r进行比较,确定⊙C与AB的关系.
D
三、新知运用
例题1、在RtΔABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1) r=2cm; (2) r=2.4cm; (3) r=3cm.
D
解:过C作CD⊥AB,垂足为D,在RtΔABC中,
根据三角形的面积公式有
CD=
即圆心C到AB的距离d=2.4cm
①当r=2cm时,由d> r,因此⊙C和AB相离.
②当r=2.4cm时,由d= r,因此⊙C和AB相切.
③当r=3cm时,由d< r,因此⊙C和AB相交.
1:在上题中,若以点C为圆心的圆与斜边AB没有公共点,则⊙C的半径的取值范围是什么?
D
答:没公共点
将“没有公共点”,改成“两个公共点”呢?
2:在上题中,若⊙C与边AB只有一个公共点,则圆半径r应取怎样的值?
答: .
或
或 .
两个公共点
变式
已知:如图所示,∠AOB= ,M为OB上一点,以M为圆
心, 5cm长为半径作圆,若M在OB上运动,问:
① 当OM满足 时,⊙M与OA相离.
四、拓展提高
② 当OM满足 时,⊙M与OA相切.
③ 当OM满足 时,⊙M与OA相交.
本节课学习了哪些知识 ?
直线与圆的位置关系
公共点个数
圆心到直线距离d与半径r的关系
公共点的名称
直线名称
1、填表形成结构
五、自主小结
2
1
0
d = r
d > r
割线
交点
切点
无
切线
无
相交
相切
相离
五、自主小结
2、判定直线与圆的位置关系的方法有两种:
(1)根据定义,由直线与圆的公共点的个数来判断;
(2)根据性质,由圆心到直线的距离d与半径r的关系
来判断.
3、切线的判定定理.
经过半径的外端且垂直于这条半径的直线是圆的切线.
六、回家作业
1、阅读课本P19~21.
2、练习册:27.4
3、选做:已知点P到直线的距离为3,以点P为圆心、r为半径画圆,
(1)如果圆上有且只有一个点到直线的距离为2,求半径r 的值.
(2)如果圆上有且只有两个点到直线的距离均为2,求半径r 的取值范围.
