沪科版七年级数学下册课件:8.2.2 第2课时 多项式除以单项式(共15张ppt)
文档属性
| 名称 | 沪科版七年级数学下册课件:8.2.2 第2课时 多项式除以单项式(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 21:08:57 | ||
图片预览



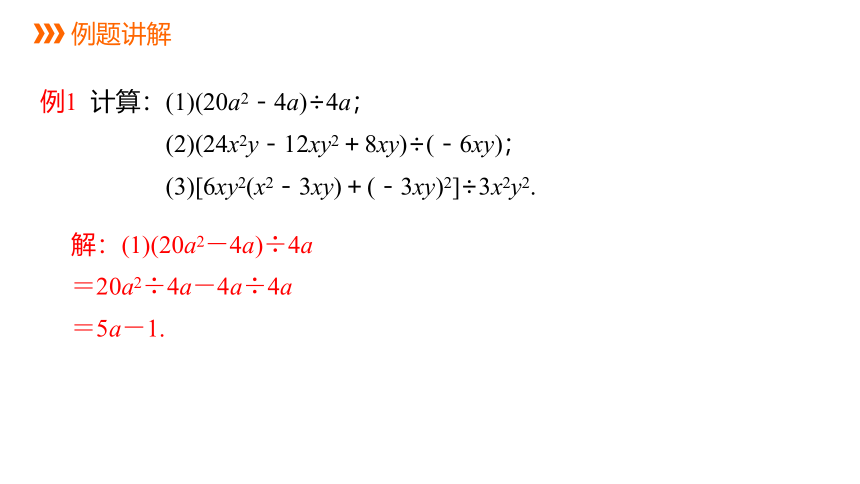
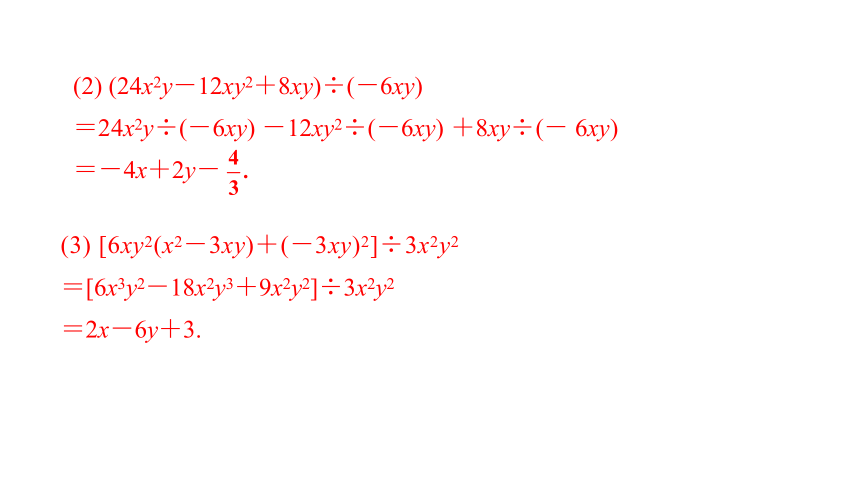

文档简介
第8章 整式乘法与因式分解
8.2.2 第2课时 多项式除以单项式
知识回顾
1.用字母表示幂的运算性质:
2.单项式除以单项式法则:
1.系数
2.同底数幂
3.只在被除式里的幂
相除;
相除;
不变;
获取新知
如何计算(a+b-c)÷m?
根据a÷b=a× 可把除法转化为乘法,由此得到
思考
(a+b-c)÷m=(a+b-c)×
= a +b -c
=a÷m+b÷m-c÷m.
归纳总结
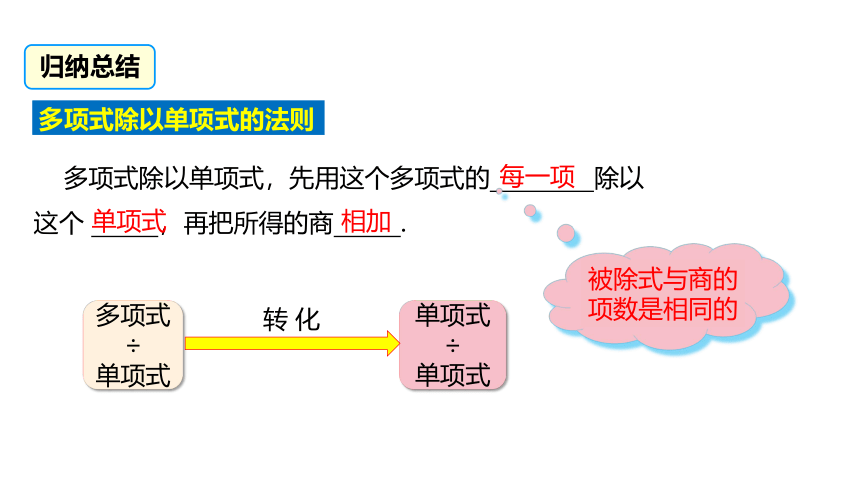
多项式除以单项式的法则
多项式除以单项式,先用这个多项式的 除以这个 ,再把所得的商 .
单项式
相加
每一项
多项式
÷
单项式
单项式
÷
单项式
转 化
被除式与商的项数是相同的
例题讲解
例1 计算:(1)(20a2-4a)÷4a;
(2)(24x2y-12xy2+8xy)÷(-6xy);
(3)[6xy2(x2-3xy)+(-3xy)2]÷3x2y2.
解:(1)(20a2-4a)÷4a
=20a2÷4a-4a÷4a
=5a-1.
(2) (24x2y-12xy2+8xy)÷(-6xy)
=24x2y÷(-6xy) -12xy2÷(-6xy) +8xy÷(- 6xy)
=-4x+2y-
(3) [6xy2(x2-3xy)+(-3xy)2]÷3x2y2=[6x3y2-18x2y3+9x2y2]÷3x2y2
=2x-6y+3.
例2 先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2017,y=2016.
解:[2x(x2y-xy2)+xy(xy-x2)]÷x2y
=[2x3y-2x2y2+x2y2-x3y]÷x2y
=x-y.
当x=2017,y=2016时,
原式=x-y=2017-2016=1.
例3 小明在爬一小山时,第一阶段的平均速度为v,所用时间为 t1;第二阶段的平均速度为 v,所用时间为t2.下山时,小明的平均速度保持为4v.已知小明上山的路程和下山的路程是相同的,问小明下山用了多长时间?
解:( vt2+vt1)÷4v=
t2+ vt1
答:小明下山所用时间为 t2+ t1
随堂演练
1.下列计算正确的是( ) A.(x3+x4)÷x3=x4 B.(-7x3-8x2+x)÷x=-7x2-8x C.(2x2+x6)÷x2=2+x4 D.(ab2-4a3b4)÷2ab=b-2a2b3
C
2.5x3y2与一个多项式的积为20x5y2-15x3y4+70(x2y3)2,
则这个多项式为( )
A.4x2-3y2 B.4x2y-3xy2
C.4x2-3y2+14xy4 D.4x2-3y2+7xy3
C
3.计算:(4x2y2-2x3y)÷(-2xy)= ÷(-2xy)+ ÷(-2xy)
= .
4x2y2
-2x3y
-2xy+x2
4.计算 (1) (9a3-21a2+6a)÷(-3a);
(2)
解:(1)原式=(9a3)÷(-3a)+(-21a2)÷(-3a)+6a÷(-3a)
=-3a2+7a-2;
(2)原式
5. 已知2a-b=6,求代数式[(a2+b2)+2b(a-b)-a(a-2b)-b2]÷4b的值.
解:原式=[a2+b2+2ab-2b2-a2+2ab-b2]÷4b
=(-2b2+4ab)÷4b
=- b+a= (2a-b)= ×6=3.
6. 一天数学课上,老师讲了整式的除法运算,放学后,王华回
到家拿出课堂笔记,认真地复习课上老师讲的内容,他突然发
现一道三项式除法运算题:(21x4y3-■+7x2y2)÷(-7x2y)=■+
5xy-y,被除式的第二项被钢笔水弄污了,商式的第一项也被
钢笔水弄污了,你能复原这两处被弄污的内容吗?
解:因为21x4y3÷(-7x2y)=-3x2y2,而且商式中未弄污的部
分没有这一项,所以商式中被弄污的内容就是-3x2y2;
因为(5xy-y)·(-7x2y)=-35x3y2+7x2y2,
所以被除式中被弄污的部分为35x3y2.
课堂小结
多项式
÷
单项式
运算法则
用这个多项式的每一项除以这个单项式,再把所得的商相加.
注意
1.计算时,商的每一项的符号是有多项式的每一项的符号和单项式的符号共同决定;(被除式与商项数一致)
2.当被除式的项与除式的项相同时,商是1,不能把“1”漏掉.
8.2.2 第2课时 多项式除以单项式
知识回顾
1.用字母表示幂的运算性质:
2.单项式除以单项式法则:
1.系数
2.同底数幂
3.只在被除式里的幂
相除;
相除;
不变;
获取新知
如何计算(a+b-c)÷m?
根据a÷b=a× 可把除法转化为乘法,由此得到
思考
(a+b-c)÷m=(a+b-c)×
= a +b -c
=a÷m+b÷m-c÷m.
归纳总结
多项式除以单项式的法则
多项式除以单项式,先用这个多项式的 除以这个 ,再把所得的商 .
单项式
相加
每一项
多项式
÷
单项式
单项式
÷
单项式
转 化
被除式与商的项数是相同的
例题讲解
例1 计算:(1)(20a2-4a)÷4a;
(2)(24x2y-12xy2+8xy)÷(-6xy);
(3)[6xy2(x2-3xy)+(-3xy)2]÷3x2y2.
解:(1)(20a2-4a)÷4a
=20a2÷4a-4a÷4a
=5a-1.
(2) (24x2y-12xy2+8xy)÷(-6xy)
=24x2y÷(-6xy) -12xy2÷(-6xy) +8xy÷(- 6xy)
=-4x+2y-
(3) [6xy2(x2-3xy)+(-3xy)2]÷3x2y2=[6x3y2-18x2y3+9x2y2]÷3x2y2
=2x-6y+3.
例2 先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2017,y=2016.
解:[2x(x2y-xy2)+xy(xy-x2)]÷x2y
=[2x3y-2x2y2+x2y2-x3y]÷x2y
=x-y.
当x=2017,y=2016时,
原式=x-y=2017-2016=1.
例3 小明在爬一小山时,第一阶段的平均速度为v,所用时间为 t1;第二阶段的平均速度为 v,所用时间为t2.下山时,小明的平均速度保持为4v.已知小明上山的路程和下山的路程是相同的,问小明下山用了多长时间?
解:( vt2+vt1)÷4v=
t2+ vt1
答:小明下山所用时间为 t2+ t1
随堂演练
1.下列计算正确的是( ) A.(x3+x4)÷x3=x4 B.(-7x3-8x2+x)÷x=-7x2-8x C.(2x2+x6)÷x2=2+x4 D.(ab2-4a3b4)÷2ab=b-2a2b3
C
2.5x3y2与一个多项式的积为20x5y2-15x3y4+70(x2y3)2,
则这个多项式为( )
A.4x2-3y2 B.4x2y-3xy2
C.4x2-3y2+14xy4 D.4x2-3y2+7xy3
C
3.计算:(4x2y2-2x3y)÷(-2xy)= ÷(-2xy)+ ÷(-2xy)
= .
4x2y2
-2x3y
-2xy+x2
4.计算 (1) (9a3-21a2+6a)÷(-3a);
(2)
解:(1)原式=(9a3)÷(-3a)+(-21a2)÷(-3a)+6a÷(-3a)
=-3a2+7a-2;
(2)原式
5. 已知2a-b=6,求代数式[(a2+b2)+2b(a-b)-a(a-2b)-b2]÷4b的值.
解:原式=[a2+b2+2ab-2b2-a2+2ab-b2]÷4b
=(-2b2+4ab)÷4b
=- b+a= (2a-b)= ×6=3.
6. 一天数学课上,老师讲了整式的除法运算,放学后,王华回
到家拿出课堂笔记,认真地复习课上老师讲的内容,他突然发
现一道三项式除法运算题:(21x4y3-■+7x2y2)÷(-7x2y)=■+
5xy-y,被除式的第二项被钢笔水弄污了,商式的第一项也被
钢笔水弄污了,你能复原这两处被弄污的内容吗?
解:因为21x4y3÷(-7x2y)=-3x2y2,而且商式中未弄污的部
分没有这一项,所以商式中被弄污的内容就是-3x2y2;
因为(5xy-y)·(-7x2y)=-35x3y2+7x2y2,
所以被除式中被弄污的部分为35x3y2.
课堂小结
多项式
÷
单项式
运算法则
用这个多项式的每一项除以这个单项式,再把所得的商相加.
注意
1.计算时,商的每一项的符号是有多项式的每一项的符号和单项式的符号共同决定;(被除式与商项数一致)
2.当被除式的项与除式的项相同时,商是1,不能把“1”漏掉.
