5.4y=a(x-h)2+k的图像和性质 课件(共18张PPT)
文档属性
| 名称 | 5.4y=a(x-h)2+k的图像和性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 293.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 19:21:14 | ||
图片预览




文档简介
x
y
1
1
2
2
3
3
4
4
5
5
6
7
-1
-1
-2
-3
-4
-5
0
-2
5.4二次函数
y=a(x-h)2+k的图像和性质
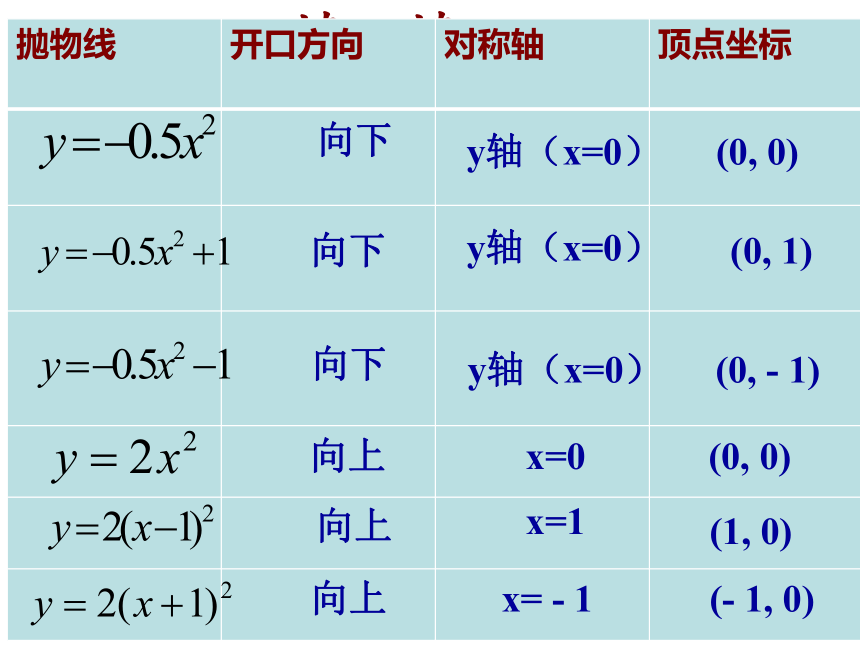
填一填
抛物线
开口方向
对称轴
顶点坐标
(0, 0)
(1, 0)
(- 1, 0)
(0, 0)
(0, 1)
(0, - 1)
向下
向下
向下
向上
向上
向上
y轴(x=0)
x=0
x=1
x= - 1
y轴(x=0)
y轴(x=0)
互助导学提纲
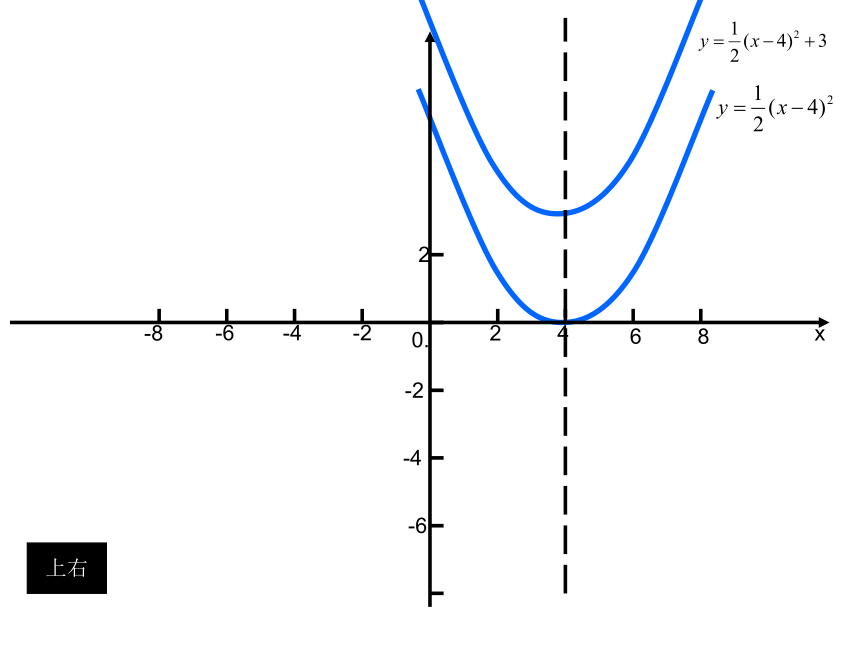
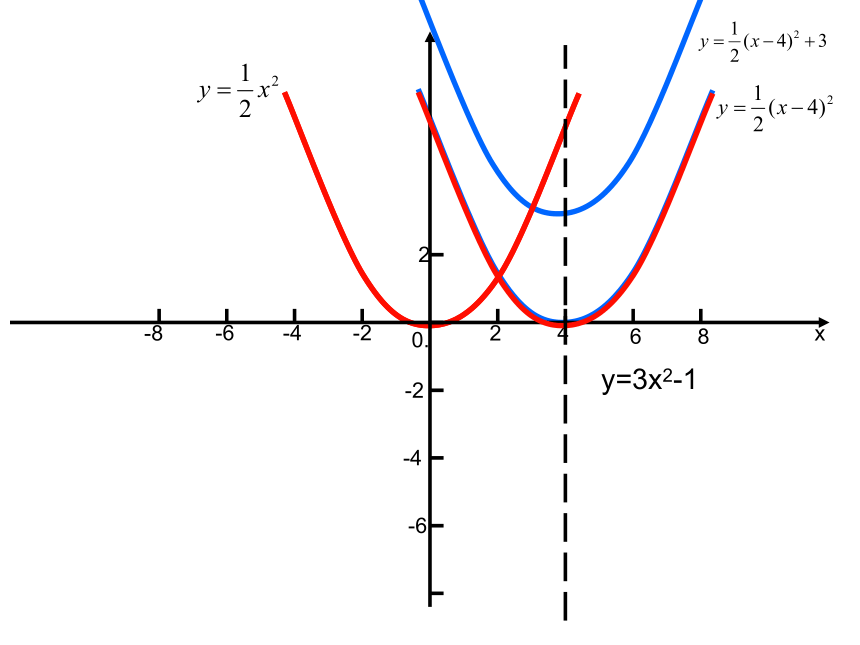
1、观察课本P37图5-27,由二次函数 的图像,经过怎样的平移,可以得到 的图像?
2、由二次函数 的图像,如果沿x轴方向和y轴方向依次进行怎样的平移,可以得到 的图像?
2
2
4
6
-2
-4
-6
0.
x
-8
8
-2
-4
-6
上右
2
2
4
6
-2
-4
-6
0.
x
-8
8
-2
-4
-6
y=3x2-1
2
2
4
6
-2
-4
-6
0.
x
-8
8
-2
-4
-6
y=3x2-1
右上
观看微课视频,思考图像之间的平移规律,
二次函数二次函数y=a(x-h)2+k的图象有哪些
性质?
向左平移1个单位
向下平移1个单位
向左平移1个单位
向下平移1个单位
平移方法1:
平移方法2:
二次函数图像平移
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x=-1
(2)抛物线
有什么关系?
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
直线x=-1
讨论
顶点是(-1, -1).
抛物线
的开口方向、对称轴、顶点?
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–5
–4
–3
–2
–1
y=2x2
y=2(x–1)2
y=2(x–1)2+1
比较y=2x2、y=2(x-1)2、 y=2(x-1)2+1 的图象
归纳
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向右(左)平移,可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h、k的值来决定.
向左(右)平移|h|个单位
向上(下)平移|k|个单位
y=ax2
y=a(x-h)2
y=a(x-h)2+k
y=ax2
y=a(x-h)2+k
向上(下)平移|k|个单位
y=ax2+k
向左(右)平移|h|个单位
平移方法:
1、要从抛物线y=2x2得到y=2(x-1)2+3的图象,则抛物线y=2x2必须( )
(A)向左平移1个单位,再向上平移3个单位.
(B)向左平移1个单位,再向下平移3个单位.
(C)向右平移1个单位,再向上平移3个单位.
(D)向右平移1个单位,再向下平移3个单位.
2、二次函数 的图像向左平移2个单位,向下平移3个单位,所得新函数表达式为( )
A.y=a(x-2)2+3 B.y=a(x-2)2-3
C.y=a(x+2)2+3 D.y=a(x+2)2-3
练一练
二次函数y=a(x-h)2+k的图象和性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
梳理总结
说出下列抛物线的开口方向、对称轴及顶点:
开口向上
对称轴是x=-3
顶点是(-3,5)
开口向下
对称轴是x=1
顶点是(1,-2)
开口向上
对称轴是x=3
顶点是(3,7)
开口向下
对称轴是x=-2
顶点是(-2,-6)
练一练
谈收获:
1、内容上:我们已经学习了哪些形式的二次函数的图像与性质,他们之间有什么关系?
2、思想方法上:
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移
左右平移
上下平移
左右平移
结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。
各种形式的二次函数的关系
要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
学以致用
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)y=ax?+c(a≠0,b=0,c≠0).
(3)y=ax?+bx (a≠0,b≠0,c=0).
2.判断一个函数为二次函数的方法与步骤:
(1)先将函数进行整理,使其右边是含自变量的代数式,左边是因变量;
(2)判别含自变量的代数式是否为整式
(3)判别含自变量的项的最高次数是否为2;
(4)判别二次项的系数是否为0。
y
1
1
2
2
3
3
4
4
5
5
6
7
-1
-1
-2
-3
-4
-5
0
-2
5.4二次函数
y=a(x-h)2+k的图像和性质
填一填
抛物线
开口方向
对称轴
顶点坐标
(0, 0)
(1, 0)
(- 1, 0)
(0, 0)
(0, 1)
(0, - 1)
向下
向下
向下
向上
向上
向上
y轴(x=0)
x=0
x=1
x= - 1
y轴(x=0)
y轴(x=0)
互助导学提纲
1、观察课本P37图5-27,由二次函数 的图像,经过怎样的平移,可以得到 的图像?
2、由二次函数 的图像,如果沿x轴方向和y轴方向依次进行怎样的平移,可以得到 的图像?
2
2
4
6
-2
-4
-6
0.
x
-8
8
-2
-4
-6
上右
2
2
4
6
-2
-4
-6
0.
x
-8
8
-2
-4
-6
y=3x2-1
2
2
4
6
-2
-4
-6
0.
x
-8
8
-2
-4
-6
y=3x2-1
右上
观看微课视频,思考图像之间的平移规律,
二次函数二次函数y=a(x-h)2+k的图象有哪些
性质?
向左平移1个单位
向下平移1个单位
向左平移1个单位
向下平移1个单位
平移方法1:
平移方法2:
二次函数图像平移
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x=-1
(2)抛物线
有什么关系?
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
直线x=-1
讨论
顶点是(-1, -1).
抛物线
的开口方向、对称轴、顶点?
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–5
–4
–3
–2
–1
y=2x2
y=2(x–1)2
y=2(x–1)2+1
比较y=2x2、y=2(x-1)2、 y=2(x-1)2+1 的图象
归纳
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向右(左)平移,可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h、k的值来决定.
向左(右)平移|h|个单位
向上(下)平移|k|个单位
y=ax2
y=a(x-h)2
y=a(x-h)2+k
y=ax2
y=a(x-h)2+k
向上(下)平移|k|个单位
y=ax2+k
向左(右)平移|h|个单位
平移方法:
1、要从抛物线y=2x2得到y=2(x-1)2+3的图象,则抛物线y=2x2必须( )
(A)向左平移1个单位,再向上平移3个单位.
(B)向左平移1个单位,再向下平移3个单位.
(C)向右平移1个单位,再向上平移3个单位.
(D)向右平移1个单位,再向下平移3个单位.
2、二次函数 的图像向左平移2个单位,向下平移3个单位,所得新函数表达式为( )
A.y=a(x-2)2+3 B.y=a(x-2)2-3
C.y=a(x+2)2+3 D.y=a(x+2)2-3
练一练
二次函数y=a(x-h)2+k的图象和性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
梳理总结
说出下列抛物线的开口方向、对称轴及顶点:
开口向上
对称轴是x=-3
顶点是(-3,5)
开口向下
对称轴是x=1
顶点是(1,-2)
开口向上
对称轴是x=3
顶点是(3,7)
开口向下
对称轴是x=-2
顶点是(-2,-6)
练一练
谈收获:
1、内容上:我们已经学习了哪些形式的二次函数的图像与性质,他们之间有什么关系?
2、思想方法上:
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移
左右平移
上下平移
左右平移
结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。
各种形式的二次函数的关系
要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
学以致用
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)y=ax?+c(a≠0,b=0,c≠0).
(3)y=ax?+bx (a≠0,b≠0,c=0).
2.判断一个函数为二次函数的方法与步骤:
(1)先将函数进行整理,使其右边是含自变量的代数式,左边是因变量;
(2)判别含自变量的代数式是否为整式
(3)判别含自变量的项的最高次数是否为2;
(4)判别二次项的系数是否为0。
