人教版九年级下册数学课件:27.3.1位似(16张)
文档属性
| 名称 | 人教版九年级下册数学课件:27.3.1位似(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 20:20:30 | ||
图片预览




文档简介
27.3.1 位似
一、教学目标
1、知识与技能目标:
(1)、了解图形的位似概念,会判断简单的位似图形和位似中心。
(2)、理解位似图形的性质,能利用位似将一个图形放大或缩小,解决一些简单的实际问题。
2、过程与方法目标:
采用引导、启发、合作、探究等方法,经历观察、发现、动手操作、归纳、交流等数学
活动,获得知识,形成技能,发展思维,学会学习;提高学生自主探究、合作交流和分析归纳能力。
3、情感态度价值观目标:
(1)、通过较多的社会背景素材的展现,使学生亲身经历位似图形的概念形成过程和位似图形性质的探索过程,感受数学学习内容的现实性、应用性、挑战性。
(2)、进一步体验合作互助、解决难题的情感,感受数学创造的乐趣,增进学好数学的信心。
二、教学重点和难点
1、重点:图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小。
2、难点:探索位似概念、位似图形的性质的过程及利用位似准确的把一个图形通过不同的方法放大或缩小。
三、课时安排
1课时
四、教学过程
前面我们已经学习了图形的哪些变换?
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
回顾与反思
相似:相似比.
旋转:旋转中心,旋转方向,旋转角度.(特殊地,中心对称)
翻折:轴对称与轴对称图形
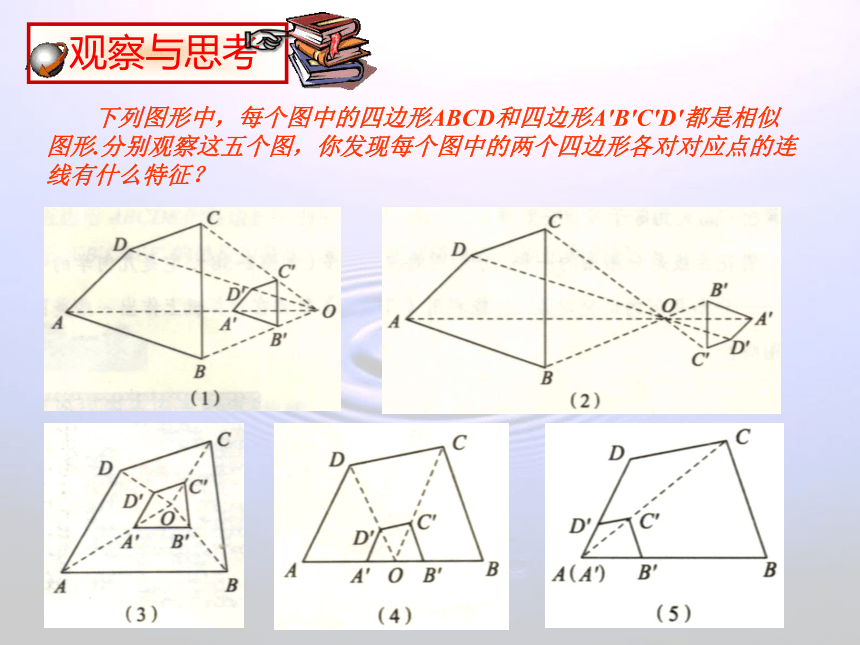
观察与思考
?
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对对应点的连线有什么特征?
概念与性质
位似图形的概念
如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
相似
对应点的连线相交一点
对应边平行
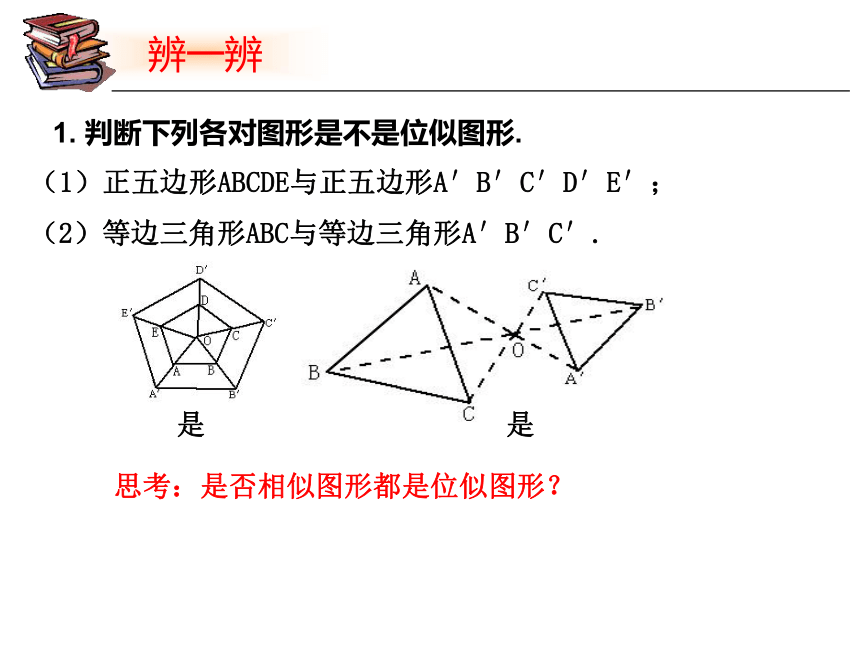
1. 判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
辨一辨
(2)等边三角形ABC与等边三角形A′B′C′.
思考:是否相似图形都是位似图形?
是
是
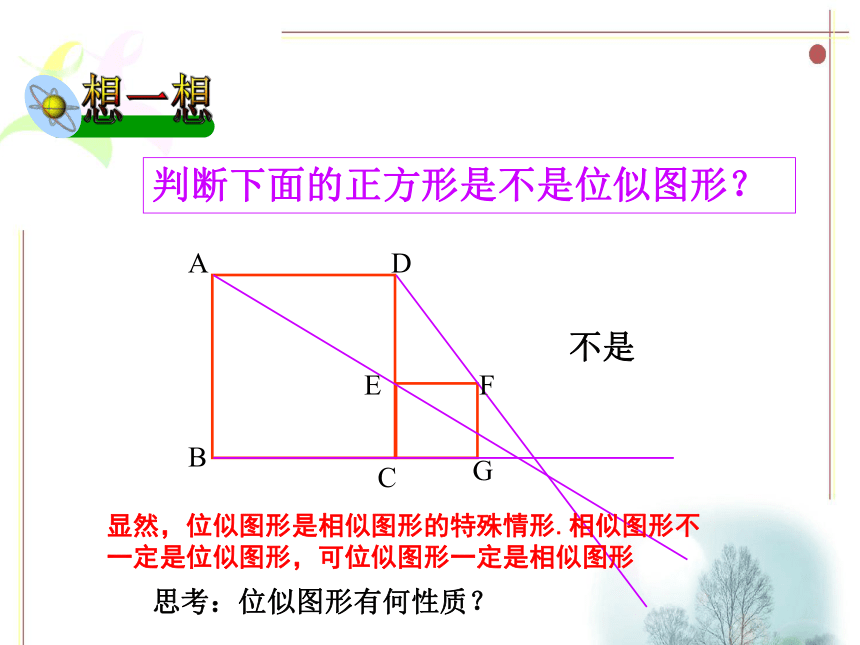
判断下面的正方形是不是位似图形?
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
2. 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
概念与性质
若△ABC与△A?B?C?的相似比为:1:2,则OA:OA?=( )。
O
A
A?
B
C
B?
C?
1:2
O
.
A
B
C
A?
C?
B?
练习与拓展
1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
OA:OA?=OB:OB? =OC:OC?= 1:2
对称点位于位似中心的同侧
.
.
.
思考:还有没其他作法?
O
.
A
B
A'
C’
B’
C
如果位似中心跑到三角形内部呢?
若对称点分居在位似中心的异侧呢?
.
.
.
如图,在已知锐角三角形ABC内作一个正方形DEFG,使点E、F在BC边上,点D在AB边上,点G在AC边上。(不写作法,只要求正确作出图形)
.
E1
D1
F1
G1
G
D
E
F
已知锐角?ABC,求作矩形MNPQ,使NP在BC上,点M和点Q分别在AB、AC上,且使MN:NP=1:2。
回味无穷
位似图形的概念:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:
1.位似图形上的任意一对对应点到位似中心的距离之比等于位似比
课堂小结
作业:完成思考题以及课本65页第2题
一、教学目标
1、知识与技能目标:
(1)、了解图形的位似概念,会判断简单的位似图形和位似中心。
(2)、理解位似图形的性质,能利用位似将一个图形放大或缩小,解决一些简单的实际问题。
2、过程与方法目标:
采用引导、启发、合作、探究等方法,经历观察、发现、动手操作、归纳、交流等数学
活动,获得知识,形成技能,发展思维,学会学习;提高学生自主探究、合作交流和分析归纳能力。
3、情感态度价值观目标:
(1)、通过较多的社会背景素材的展现,使学生亲身经历位似图形的概念形成过程和位似图形性质的探索过程,感受数学学习内容的现实性、应用性、挑战性。
(2)、进一步体验合作互助、解决难题的情感,感受数学创造的乐趣,增进学好数学的信心。
二、教学重点和难点
1、重点:图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小。
2、难点:探索位似概念、位似图形的性质的过程及利用位似准确的把一个图形通过不同的方法放大或缩小。
三、课时安排
1课时
四、教学过程
前面我们已经学习了图形的哪些变换?
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
回顾与反思
相似:相似比.
旋转:旋转中心,旋转方向,旋转角度.(特殊地,中心对称)
翻折:轴对称与轴对称图形
观察与思考
?
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对对应点的连线有什么特征?
概念与性质
位似图形的概念
如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
相似
对应点的连线相交一点
对应边平行
1. 判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
辨一辨
(2)等边三角形ABC与等边三角形A′B′C′.
思考:是否相似图形都是位似图形?
是
是
判断下面的正方形是不是位似图形?
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
2. 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
概念与性质
若△ABC与△A?B?C?的相似比为:1:2,则OA:OA?=( )。
O
A
A?
B
C
B?
C?
1:2
O
.
A
B
C
A?
C?
B?
练习与拓展
1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
OA:OA?=OB:OB? =OC:OC?= 1:2
对称点位于位似中心的同侧
.
.
.
思考:还有没其他作法?
O
.
A
B
A'
C’
B’
C
如果位似中心跑到三角形内部呢?
若对称点分居在位似中心的异侧呢?
.
.
.
如图,在已知锐角三角形ABC内作一个正方形DEFG,使点E、F在BC边上,点D在AB边上,点G在AC边上。(不写作法,只要求正确作出图形)
.
E1
D1
F1
G1
G
D
E
F
已知锐角?ABC,求作矩形MNPQ,使NP在BC上,点M和点Q分别在AB、AC上,且使MN:NP=1:2。
回味无穷
位似图形的概念:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:
1.位似图形上的任意一对对应点到位似中心的距离之比等于位似比
课堂小结
作业:完成思考题以及课本65页第2题
