人教版七年级数学下册 5.3.1 平行线的性质 课件(19张)
文档属性
| 名称 | 人教版七年级数学下册 5.3.1 平行线的性质 课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 920.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 20:15:23 | ||
图片预览




文档简介
5.3.1 平行线的性质
掌握平行线的三个性质;
会用平行线的性质进行有关的简单推理和计算;
通过对比,理解平行线的性质和判定的区别。
学习目标
1、如果两个数的和为0,这两个数互为相反数。
2、对顶角相等。
√
√
√
如果一个句子是正确的,反过来说
(因果对调),就未必正确。
困惑:反过来说也对吗?
反过来,如果这两个数互为相反数,那么这两个数和为0。
反过来,如果两个角相等,那么这两个角是对顶角。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
如果一个句子是正确的,反过来说
(因果对调),就未必正确。
困惑:反过来怎么说?它还对吗?
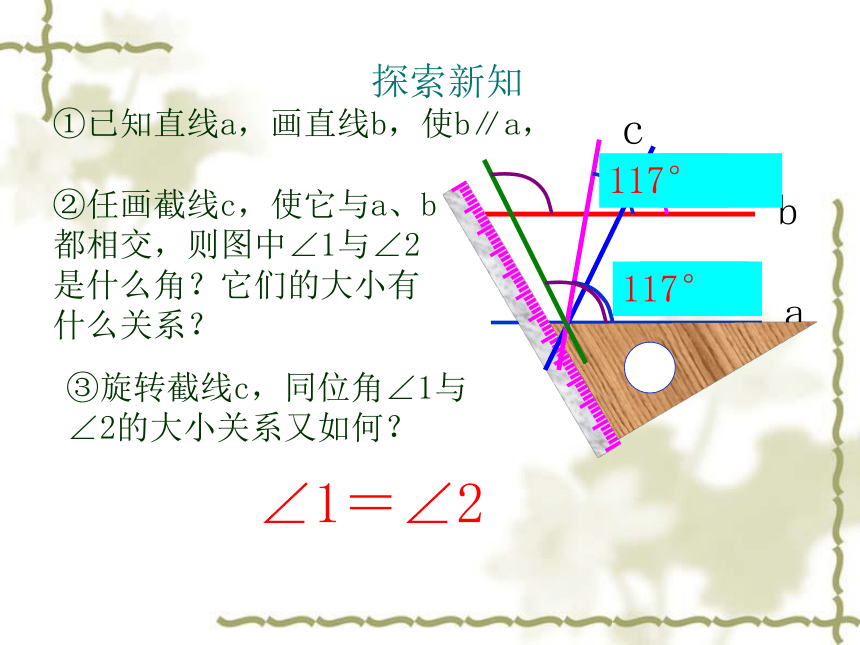
①已知直线a,画直线b,使b∥a,
a
b
②任画截线c,使它与a、b都相交,则图中∠1与∠2是什么角?它们的大小有什么关系?
1
2
58°
58°
82°
82°
117°
117°
③旋转截线c,同位角∠1与∠2的大小关系又如何?
∠1=∠2
c
探索新知
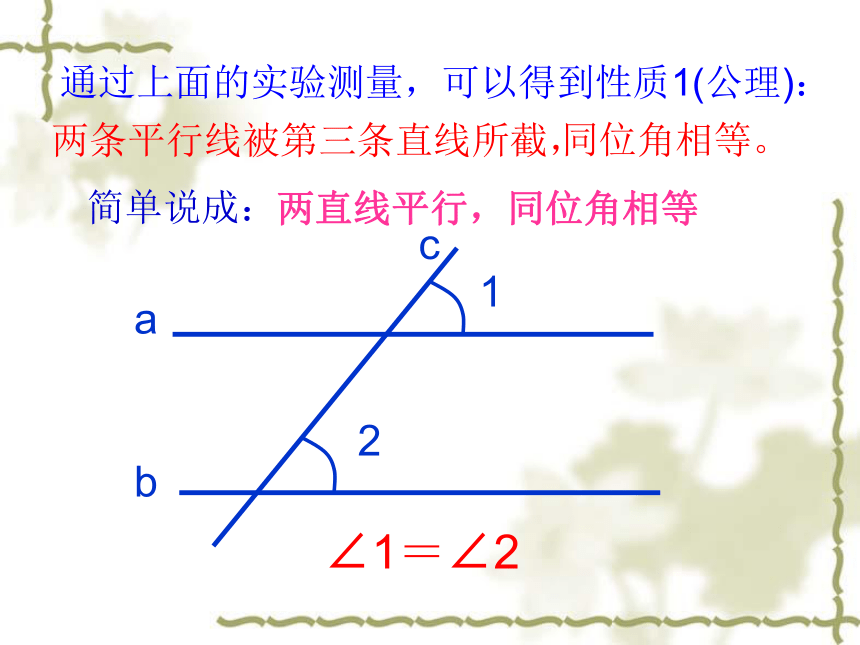
两条平行线被第三条直线所截,
同位角相等。
1
2
a
b
∠1=∠2
简单说成:
两直线平行,同位角相等
c
通过上面的实验测量,可以得到性质1(公理):
a
b
c
1
2
3
理由:
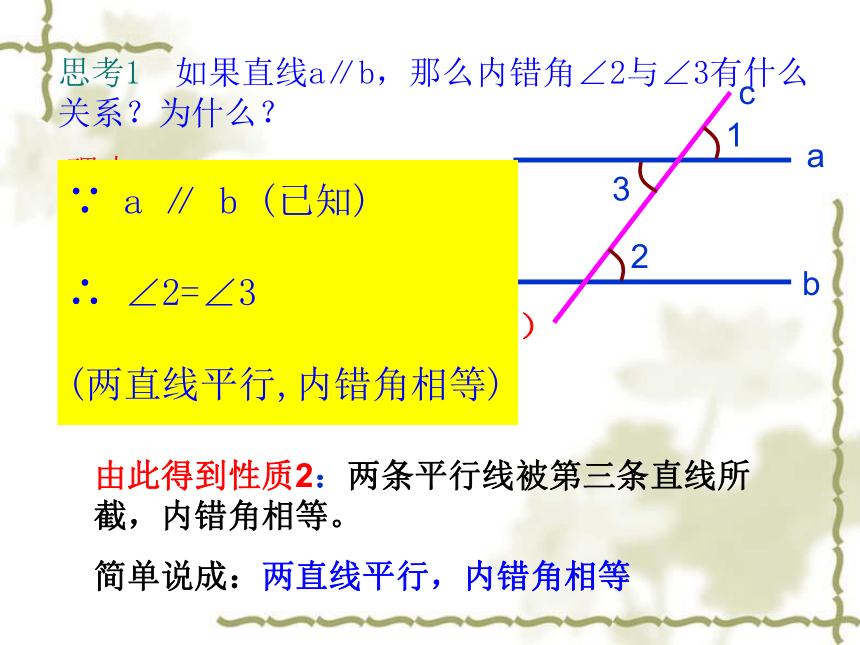
∵a∥b(已知)
∴∠1 = ∠2
(两直线平行,同位角相等)
又∵ ∠1 = ∠3
∴ ∠2 = ∠3
由此得到性质2:两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等
(对顶角相等)
(等量代换)
∵ a ∥ b (已知)
∴ ∠2=∠3
(两直线平行,内错角相等)
思考1 如果直线a∥b,那么内错角∠2与∠3有什么关系?为什么?
a
b
c
1
2
3
4
理由:
∵a∥b(已知)
∴∠1 = ∠2
(两直线平行,同位角相等)
又∵ ∠1 + ∠4=180°
∴∠2 +∠4=180°(等量代换)
由此得到性质3:两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补
(邻补角定义)
∵ a ∥ b (已知)
∴ ∠2+∠4=180°
(两直线平行,同旁内角互补)
思考2 如果直线a∥b,那么同旁内角∠2与∠4有什么关系?为什么?
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等
简单说成:两直线平行,同位角相等
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补
精彩回放
A
B
C
D
解:∵AD∥BC (已知)
∴? A +? B=180°
(两直线平行,同旁内角互补)
即 ∠B= 180°-? A=180°-115°=65°
∵AD∥BC (已知)
∴? D+ ? C=180°
(两直线平行,同旁内角互补)
即? C=180°-? D =180°-100°=80°
答:梯形的另外两个角分别为65°、80°
如图有一块梯形的玻璃,已知量得∠A=115°,∠D=100°,请你想一想,梯形的另外两个角各是多少度。
B
C
A
D
解∵AB∥CD
(已知)
∴∠B=∠C
(两直线平行,内错角相等)
又∵∠B=142°
∴∠C=∠B=142°
(已知)
(等量代换)
一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同(即拐弯前后的两条路互相平行),若测得第一次拐弯的∠B是142°,则第二次拐弯的∠C应是多少度才合理?为什么?
①两直线被第三条直线所截,同位角相等。
②两直线平行,同旁内角相等。
③“内错角相等,两直线平行”是平行线的性质。
④“两直线平行,同旁内角互补”是平行线的性质。
×
√
×
×
判断下列语句是否正确
A
B
C
D
4、(1)当______∥______时,∠ABD=∠CDB;
(2)当_______∥_______时,∠ADB=∠ CBD;
(3)当_______∥_______时,∠BAC=∠DCA;
(4)当_______+_______=180°时,AD∥BC
(5)当_______∥_______时,∠BAD+∠ADC=180°
3、当AB∥CD时,则下列结论成立的是( )
∠DAC=∠ACB (B) ∠DAB+∠ABC=180°
(C)∠ADB=∠DBC (D) ∠BAC=∠ACD
D
AB
CD
AD
BC
AB
CD
∠DAB
∠ABC
AB
CD
①DE、BC平行吗?为什么?
②∠C等于多少度?为什么?
A
C
B
E
D
解:∵∠ADE=60°,∠B=60°
(同位角相等,两直线平行)
(两直线平行,同位角相等)
(等量代换)
∴∠ADE=∠B
∴DE∥BC
∴∠C=∠AED
又∵∠AED=80°(已知)
∴∠C=80°
如图,已知D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=80°.
⌒
⌒
A
B
C
D
E
60°
32°
1
2
F
解:过E作EF//AB
因为AB//CD
所以EF//CD
所以∠1=∠B=60°
所以∠2=∠D=32°
所以∠BED=∠1+ ∠2 =60°+ 32°= 92°
已知:如图AB∥CD, ∠ABE= 60°, ∠CDE= 32°,求∠BED的度数.
因为∠1=∠2
所以AB//CD
所以∠3=∠A
因为∠A=∠C
所以∠3=∠C
所以AE∥BC
解:
(已知)
(同位角相等,两直线平行)
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
例2:已知:如图∠1=∠2, ∠A=∠C,说明:AE∥BC
解:因为CE⊥AB, DF⊥AB
所以DF//EC
所以∠BDF=∠1,
∠EDF=∠3
因为ED//AC,
所以∠3=∠2
所以∠EDF=∠2
又CE平分∠ACB
所以∠1=∠2
所以∠BDF=∠EDF
1
3
2
如图,在?ABC中,CE⊥AB于点E,DF⊥AB于点F,AC//ED,CE是∠ACB的平分线,则∠EDF=∠BDF,请说明理由。
图形
已知
结果
结论
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
同位角相等
两直线平行
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
平行线的性质
同
位
角
内
错
角
同旁
内角
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由___________得到_____________的结论是平行线的判定;
请注意:
2.由____________得到________________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
证两直线平行
两直线平行
角相等或互补
证角相等或互补
小结
掌握平行线的三个性质;
会用平行线的性质进行有关的简单推理和计算;
通过对比,理解平行线的性质和判定的区别。
学习目标
1、如果两个数的和为0,这两个数互为相反数。
2、对顶角相等。
√
√
√
如果一个句子是正确的,反过来说
(因果对调),就未必正确。
困惑:反过来说也对吗?
反过来,如果这两个数互为相反数,那么这两个数和为0。
反过来,如果两个角相等,那么这两个角是对顶角。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
如果一个句子是正确的,反过来说
(因果对调),就未必正确。
困惑:反过来怎么说?它还对吗?
①已知直线a,画直线b,使b∥a,
a
b
②任画截线c,使它与a、b都相交,则图中∠1与∠2是什么角?它们的大小有什么关系?
1
2
58°
58°
82°
82°
117°
117°
③旋转截线c,同位角∠1与∠2的大小关系又如何?
∠1=∠2
c
探索新知
两条平行线被第三条直线所截,
同位角相等。
1
2
a
b
∠1=∠2
简单说成:
两直线平行,同位角相等
c
通过上面的实验测量,可以得到性质1(公理):
a
b
c
1
2
3
理由:
∵a∥b(已知)
∴∠1 = ∠2
(两直线平行,同位角相等)
又∵ ∠1 = ∠3
∴ ∠2 = ∠3
由此得到性质2:两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等
(对顶角相等)
(等量代换)
∵ a ∥ b (已知)
∴ ∠2=∠3
(两直线平行,内错角相等)
思考1 如果直线a∥b,那么内错角∠2与∠3有什么关系?为什么?
a
b
c
1
2
3
4
理由:
∵a∥b(已知)
∴∠1 = ∠2
(两直线平行,同位角相等)
又∵ ∠1 + ∠4=180°
∴∠2 +∠4=180°(等量代换)
由此得到性质3:两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补
(邻补角定义)
∵ a ∥ b (已知)
∴ ∠2+∠4=180°
(两直线平行,同旁内角互补)
思考2 如果直线a∥b,那么同旁内角∠2与∠4有什么关系?为什么?
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等
简单说成:两直线平行,同位角相等
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补
精彩回放
A
B
C
D
解:∵AD∥BC (已知)
∴? A +? B=180°
(两直线平行,同旁内角互补)
即 ∠B= 180°-? A=180°-115°=65°
∵AD∥BC (已知)
∴? D+ ? C=180°
(两直线平行,同旁内角互补)
即? C=180°-? D =180°-100°=80°
答:梯形的另外两个角分别为65°、80°
如图有一块梯形的玻璃,已知量得∠A=115°,∠D=100°,请你想一想,梯形的另外两个角各是多少度。
B
C
A
D
解∵AB∥CD
(已知)
∴∠B=∠C
(两直线平行,内错角相等)
又∵∠B=142°
∴∠C=∠B=142°
(已知)
(等量代换)
一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同(即拐弯前后的两条路互相平行),若测得第一次拐弯的∠B是142°,则第二次拐弯的∠C应是多少度才合理?为什么?
①两直线被第三条直线所截,同位角相等。
②两直线平行,同旁内角相等。
③“内错角相等,两直线平行”是平行线的性质。
④“两直线平行,同旁内角互补”是平行线的性质。
×
√
×
×
判断下列语句是否正确
A
B
C
D
4、(1)当______∥______时,∠ABD=∠CDB;
(2)当_______∥_______时,∠ADB=∠ CBD;
(3)当_______∥_______时,∠BAC=∠DCA;
(4)当_______+_______=180°时,AD∥BC
(5)当_______∥_______时,∠BAD+∠ADC=180°
3、当AB∥CD时,则下列结论成立的是( )
∠DAC=∠ACB (B) ∠DAB+∠ABC=180°
(C)∠ADB=∠DBC (D) ∠BAC=∠ACD
D
AB
CD
AD
BC
AB
CD
∠DAB
∠ABC
AB
CD
①DE、BC平行吗?为什么?
②∠C等于多少度?为什么?
A
C
B
E
D
解:∵∠ADE=60°,∠B=60°
(同位角相等,两直线平行)
(两直线平行,同位角相等)
(等量代换)
∴∠ADE=∠B
∴DE∥BC
∴∠C=∠AED
又∵∠AED=80°(已知)
∴∠C=80°
如图,已知D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=80°.
⌒
⌒
A
B
C
D
E
60°
32°
1
2
F
解:过E作EF//AB
因为AB//CD
所以EF//CD
所以∠1=∠B=60°
所以∠2=∠D=32°
所以∠BED=∠1+ ∠2 =60°+ 32°= 92°
已知:如图AB∥CD, ∠ABE= 60°, ∠CDE= 32°,求∠BED的度数.
因为∠1=∠2
所以AB//CD
所以∠3=∠A
因为∠A=∠C
所以∠3=∠C
所以AE∥BC
解:
(已知)
(同位角相等,两直线平行)
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
例2:已知:如图∠1=∠2, ∠A=∠C,说明:AE∥BC
解:因为CE⊥AB, DF⊥AB
所以DF//EC
所以∠BDF=∠1,
∠EDF=∠3
因为ED//AC,
所以∠3=∠2
所以∠EDF=∠2
又CE平分∠ACB
所以∠1=∠2
所以∠BDF=∠EDF
1
3
2
如图,在?ABC中,CE⊥AB于点E,DF⊥AB于点F,AC//ED,CE是∠ACB的平分线,则∠EDF=∠BDF,请说明理由。
图形
已知
结果
结论
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
同位角相等
两直线平行
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
平行线的性质
同
位
角
内
错
角
同旁
内角
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由___________得到_____________的结论是平行线的判定;
请注意:
2.由____________得到________________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
证两直线平行
两直线平行
角相等或互补
证角相等或互补
小结
